3.2 Синтез цифрового фильтра по заданной его ачх.

В предыдущем параграфе был синтезирован ЦФ по аналоговому прототипу с заданной передаточной функцией (т.е. с учетом АЧХ и ФЧХ) и установлена связь АЧХ ЦФ и АЧХ АФ. Из теории цепей известно, что при достаточной равномерности АЧХ аналогового фильтра, его ФЧХ практически линейна (имеется ввиду, в пределах полосы пропускания). Это даёт возможность синтезировать фильтр только по заданной АЧХ.

На этой основе можно предложить следующий порядок синтеза цифрового фильтра по заданной АЧХ :

1.Задается требуемая АЧХ цифрового фильтра в интервале частот

2.На этой характеристике находятся характерные точки

3.По ним определяются соответствующие им частоты аналогового фильтра прототипа ,исходя из правила :

4.По этим точкам строится АЧХ АФ-прототипа так, чтобы

5.Осуществляется синтез АФ по полученной АЧХ т.е. определяется его передаточная функция .

6.Используя билинейное преобразование , находим системную функцию цифрового фильтра в виде :

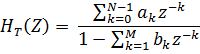
7.Определяем структуру ЦФ по системной функции

Как видим, основные проблемы при решении этой задачи свелись к синтезу АФ-прототипа по его АЧХ, т.е. к нахождению передаточной функции по функции

Из теории цепей известно, что синтез АФ по АЧХ возможен лишь в том случае, когда квадрат АЧХ является функцией квадрата частоты, т.е.

Объясним это .

АЧХ находится путем вычисления передаточной функции в точках, лежащих на мнимой оси, т.е. , .

Ранее передаточную функцию АФ записывали в виде рациональной дроби

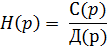
Тогда :

Это означает, что нули и полюсы передаточной функции находятся в квадрантной симметрии, т.е. каждому нулю этой функции, находящемуся в левой полуплоскости, соответствует симметричный нуль, лежащий в правой полуплоскости, а каждому полюсу, лежащему в левой полуплоскости р, соответствует симметричный полюс, лежащий в правой полуплоскости р.

Очевидно, что нули и полюсы, находящиеся в левой полуплоскости р, соответствуют функции , а нули и полюсы, находящиеся в правой полуплоскости р соответствуют функции т.е. :