Авдеев В.В.
Конспект лекций по дисциплине
«ЦИФРОВАЯ ОБРАБОТКА СИГНАЛОВ»
для студентов, обучающихся по направлению подготовки бакалавров
210400 «Радиотехника»
Рязань 2014г.
Раздел 1. Основы теории цифровой линейной фильтрации сигнала.
1.1. Понятие дискретной и цифровой линейной фильтрации аналогового сигнала.
Ранее в курсах ОТЦ и РТЦиС линейной фильтрацией называлась аналоговая линейная фильтрация (АФ), преобразующая аналоговый сигнал s1(t) в аналоговый сигнал s2(t).
Рис. 1.
При дискретной линейной фильтрации аналоговый сигнал s1(t) сначала преобразуется с помощью идеального временного дискретизатора (ВД) в дискретный сигнал s1т(t)
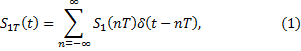
– отсчет аналогового сигнала 
Рис. 2.
Период временной дискретизации должен соответствовать требованиям теоремы Котельникова В.А., то есть
где
–верхняя граничная частота в спектре
сигнала s1(t).
Непосредственно в дискретном фильтре (ДФ) осуществляются необходимые линейные операции, преобразующие дискретный сигнал s1т(t) в дискретный сигнал s2т(t), или другими словами, совокупность отсчетов {s1(nТ)} в совокупность отсчетов {s2(nТ)}.
Если
отклик фильтра требуется получить в
аналоговой форме, то после дискретной
фильтрации осуществляют преобразование
дискретного сигнала s2т(t)
в аналоговый сигнал
s2(t),
то есть осуществляют восстановление
аналогового сигнала по его дискретным
отсчетам {s2(nТ)}
с помощью сглаживающего (восстанавливающего)
фильтра (СФ) – идеального фильтра НЧ,
полоса пропускания которого 2
fфНЧ=2fв,
т.е. в соответствии с теоремой Котельникова
В.А.
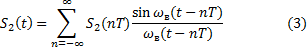
В результате сказанного структурная схема дискретной линейной фильтрации аналогового сигнала может быть изображена в виде:
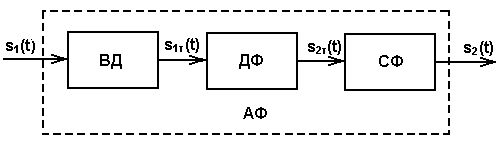
Рис. 3.
При
цифровой линейной фильтрации, в отличие
от дискретной, происходит дополнительное
преобразование отсчетов воздействия
из аналоговой формы {s1(nТ)}
в цифровую
.
Величины
принимают лишь дискретные (квантованные)
значения, каждому из которых может быть
поставлено в соответствие определенное
число, в том числе, выраженное двоичным
кодом. Такое преобразование осуществляется
устройством, называемым аналого-цифровым
преобразователем (АЦП). В результате
дискретный сигнал s1т(t)
превращается в цифровой сигнал
.
Непосредственно
в цифровом фильтре (ЦФ) осуществляются
необходимые линейные операции над
совокупностью отсчетов
,
преобразующие ее в отсчеты
или, по-другому, преобразующие цифровой
сигнал
в цифровой сигнал
.
Для
обратного преобразования цифрового
сигнала
в дискретный сигнал s2т(t)
используется устройство, называемое
цифро-аналоговым преобразователем
(ЦАП), в котором отсчеты отклика ЦФ
преобразуются из цифровой формы
в аналоговую {s2(nТ)}.
В дальнейшем, при необходимости,
дискретный сигнал s2т(t)
с помощью сглаживающего фильтра (СФ)
может быть преобразован в аналоговый
сигнал s2(t).
Исходя из сказанного, структурная схема цифровой линейной фильтрации аналогового сигнала может быть представлена в виде:
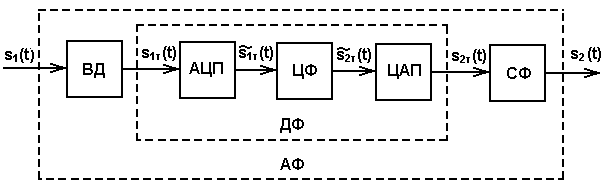
Рис. 4.
Таким образом, отличие дискретной и цифровой линейной фильтрации заключается лишь в форме представления дискретных отсчетов аналогового сигнала. Поэтому в дальнейшем анализ и синтез дискретных и цифровых линейных фильтров будем осуществлять совместно.