15.Оцінювання невідомих параметрів по емпіричній функції розподілу. Властивості оцінок.

, x= )

, Оцінка . Будь-яка функція від вибірки - статистика.

Класиф.1:оцінка невідомого параметра наз.незміщеною,якщо

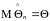
Якщо - оц.зміщенна. - зсув оцінки.

Класиф.2:незміщена оцінка невід.параметра назив.спроможною, якщо

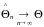
Класиф.3: незміщена оцінка невід.параметра назив. асимптотично нормальною,якщо

Класиф.4:незміщена оцінка назив. оптимальною,якщо дисперсія найменша серед усіх можливих оцінок.

Оцінка невідомого мат.сподівання:

1. - найкраща оцінка

=

Властивості оцінок:

К.1)

_К.2)

К.3)

К.4) Для більшості класичних розподілів вона буде оптимальною

- вибіркове середнє

16.Ефективні точкові оцінки. НерівністьКрамера-Рао

Нехай

- функціяправдоподібності

Лема 1.Якщо виконуютьсянаступніумови:

1. 

2. 

3. , тоді

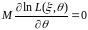
- щільн.

НерівністьКрамера-Рао:

Нехай - довільнанезалежнаоцінкафукції

Якщовиконуєтьсяумови не лише 1, а також - двічі непер.дифер., дисперсія оцінки обмежен. та

, де

Наслідок:

1). Нехай 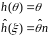- незалежна оцінка для a

Якщодисперсія незалежної оцінки дорівнює , то оцінка ефективна. Якщо для існує ефективна оцінка, то вона оптимально.

, - найкраща оцінка для

- ефективна оцінка

2). Нехай - зміщена оцінка

, тоді

Теорема:

Незм.оцінка ефективнатоді і тількитоді, коли перша похідна:

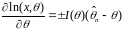
17. Достатні статистики.

Статистика, яка несе в собі всю інформацію про невідомий параметр ϴ наз. достатньою.

Т1. Критерій факторизації

Статистика 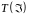достатня коли функція правдоподібна, тобто

- тривіальна достатня статистика

Доведення Необх-ть: -достатня статистика, ,

Достат-ть:

Нехай виконується

Приклад: Розподіл Пуасона:

Властивості достатніх статистик

Т2. Якщо для ϴ існує оптимальна оцінка, то вона є функцією від достатньої статистики.

- довільна незміщена статистика від ϴ.

- нетривіальна достатня статистика

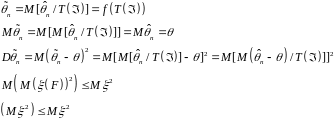
Ф-ія від достат. статистики буде найкр. оцінкою.

18. Метод моментів. Приклад.

Складемо систему рівнянь:

Якщо можна розв’язати, то є оцінка.

Приклад.

Оцінки методу моментів спроможні, асимптотично нормальні, але дуже часто зміщені та неефективні.

19.Метод максимальної правдоподібності.Приклад

, -оцінка макс. правдоподібності

-рівняння правдоподібності

Розв’язок

, -точка max.

Приклад:

;

;

; , -точка max.

Приклад:

;

1)Нехай ;

2) ;

3) ;

-оцінка max

Властивості оцінок макс правдоподібності

1)Якщо, для параметра існує достатня статистика, то оцінки МП-ф-ія достат. статистики.

- дост. ;

;

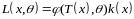
2)Нехай - скаляр.параметр. Якщо, для параметра існує ефектив. оцінки, то вона співпадає з оцінками МП.

-ефектив.; ; , - оцінка макс. МП.

20.Асимптотична нормальність оцінок максимальної правдоподібності.

Нехай , де 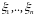- незалежні однаково розподілені випадкові величини з щільністю . Тоді

Теорема Фішера. незміщена оцінка максимальної правдоподібності, і виконані умови:

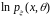тричі диференційована по ;

1. ;

2. ;

3. , тоді послідовність оцінок максимальної правдоподібності сильно спроможна асимптотична нормальна і асимптотично ефективна, тобто - асимптотична ефективність.

Доведення. - рівняння правдоподібності. оцінка правдоподібності, . - істинне значення параметра.