1.Ланцюги Маркова з неперервним часом. 3

2. Система диференційних рівнянь Колмогорова 4

3. Процеси загибелі та народження 5

4. Застосування ланцюгів Маркова в теорії масового обслуговування. 7

6. Поняття про стохастичні інтеграл Іто. Стохаст диференціал. 11

7.Стаціонарні процеси. Приклади. 14

8.Спектральна функція і спектральна щільність стаціонарного процесу. 17

9.Основні задачі математичної статистики: 18

10.Емпірична функція розподілу. Асимптотичні властивості. 20

11.Гістограма 23

12.Порядкові статистики. 25

13.Вибіркові математичне сподівання та дисперсія. 27

14.Мода та медіана. 30

15.Оцінювання невідомих параметрів по емпіричній функції розподілу. Властивості оцінок. 32

16.Ефективні точкові оцінки. НерівністьКрамера-Рао 34

18. Метод моментів. Приклад. 38

19.Метод максимальної правдоподібності.Приклад 39

20.Асимптотична нормальність оцінок максимальної правдоподібності. 41

21. Надійні інтервали. Побудова асимптотичних надійних інтервалів. Приклад. 43

22. Надійні інтервали для параметрів нормального розподілу у випадку, коли один з параметрів відомий. 46

23.Теорема про незалежність вибіркових середнього та дисперсій для нормального розподілу. 48

24.Надійні інтервали для параметрів нормального розподілу у випадку, коли обидва параметри невідомі. 51

25.Критерій X² 54

26.Критерій Xдля перевірки незалежності та однорідності. Критерій однорідності 57

27.Перевірка статистичних гіпотез. Критерій Колмогорова, Колмогорова-Смірнова. 59

28. Задача про вибір двох простих гіпотез. Лема Неймана-Пірсона. 61

29.Критерій Неймана-Пірсона для перевірки простих гіпотез про математичне сподівання для нормального розподілу. 63

30.Критерій Неймана-Пірсона для дискретних розподілів. Рандомізовані критерії. 65

31.Перевірка гіпотез про рівність математичних сподівань двох нормальних сукупностей 68

32.Перевірка гіпотез про рівність дисперсій двох вибірок з нормальних сукупностей. 70

33.Послідовний аналіз. Критерій Вальда. 72

34. Елементи кореляційного аналізу. Коефіцієнт тісноти зв’язку 76

35. Метод найменших квадратів. Лінійна регресія. 77

36. Коефіцієнти кореляції рангів Спірмена та Кендела. 79

37. Однофакторний дисперсійний аналіз. 81

38. Двофакторний дисперсійний аналіз. 83

39.Статистичні рішаючи функції. Байєсівське та мінімаксне рішення. 85

40.Оцінки параметрів та перевірки гіпотез з позиції теорії рішень. 86

41.Задача класифікації спостережень. 89

42 .Класифікація спостережень у випадку двох нормальних сукупностей. 91

43.Аналіз часових рядів. Згладжування, виділення тренду, прогнозування. 93

1.Ланцюги Маркова з неперервним часом.

Формула Чеклана-Колмогорова

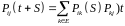
Інфінітизимальні характеристики

1. 2.

1. поглинаючий стан

2. миттєвий стан

3. затримуючий стан

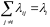регулярний ЛМ

2. Система диференційних рівнянь Колмогорова

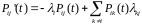- обернена система

Пряма система

при множенні на попереднє отримуємо наступну систему:

Ергодичний розподіл:

Приклад – ланцюги Маркова з неперервним часом

3. Процеси загибелі та 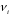народження

- інтенс. народження, - смерті

,

,

,

, ,

,

- ймовірність знаходж. в стані j

(умова ергодичності)

4. Застосування ланцюгів Маркова в теорії масового обслуговування.

Система масового обслуговування(СМО): є n приладів, на які поступають замовлення через випадковий проміжок часу; час обслуговування – випадковий;можливо: всі зайняті; n+1 створюють чергу; т місць у черзі.

A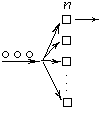 |B|n|m – СМО; A – вхідний потік замовлення, B – відповідає за обслуговування ; n- к-сть приладів; m – к-сть місць у черзі,

якщо параметр т пропущений, то черга

М|M|n|m – марківський (описується процесом смертності-народження)

М|M|n – с-ма без втрат (М|M|n|0 – формула Ерланта)

М|M|1 – 1 прилад, нескінченна черга;

параметри .

Загрузка системи ;

Якщо – ергодичний розподіл, – не ерг. розп., черга росте

– середнє число замовлень в с-мі

Середня довжина черги

М|M|n

Ергодичний розподіл –

Загрузка системи –

М|M|1|0

М|M|n|m

,

5. Умовні математичні сподівання. Властивості. Мартингали. Приклади.

Умовні мат. сподівання:

- умовна функція розподілу

- умовне мат. сподівання

Формула повної ймов. для умовного мат. сподівання:

Приклад:

– ймов. простір

Існує

Означення: умовним мат. сподіванням по сігма-алгебріназ. -вимірна вип. вел. для якої викон. рівність:

–вимірна означає

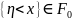
Властивості умовного мат. сподівання:

1) не залежить від

2) якщо –вимірна

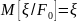
3) - –вимірна

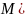
4) лінійність

5)

6)

7) якщо

Мартингали:

Є послідовність вип. вел

Пара наз. мартингалом, якщо ,

- –вимірна

– субмартингал

- супермартингал

Приклад1:

Нехай - н.в.в.

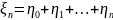
Послідовність , - мартингал

Приклад2:

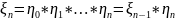
, - мартингал

Приклад3:

, - мартингал

Теорема про збіжність Дуба: якщо - субмартингал,

, тоді ,

6. Поняття про стохастичні інтеграл Іто. Стохаст диференціал.

w(t) – стандартний вінерівський процес, такий, що він - вимірний.

= Вводиться функція f(t) -вимірна, f(t) – ступінчата

Властивості інтеграла Іто:

1.

2.

3.

5.

6. w1, w2 – незалежні, f,g є M2[a,b]

Загальна f(t) є M2 [a,b] – інтегрована в квадраті.

- інтеграл Іто в загал. випадку

Стохастичний диференціал. a(t), b(t) – випадкові величини. [ t0, T ]

Стохастичнийдифер.вінерівськогопроцесу

Формула Іто:

7.Стаціонарні процеси. Приклади.

Формула Блека-Шоуза.

Нехай S(t) - ціна акцій в момент часу t, це випадковий процес, для якого справедливо:

Вип.процес наз.стаціонарним у вузькому розумінні, якщо 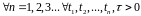розподіл вектора не залежить від .

Вип.процес наз. стаціонарним в широкому розумінні, якщо

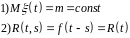
Будь-який процес у вузьк. розумінні є і в широкому.

R(t) – корел.функція стаціонарного в широкому розум.процесу

Теорема Бохнера-Хінчина

Теорема Хінчина. Неперервна ф-ія

Доведення.

Необх.

Дост.

Приклади.

8.Спектральна функція і спектральна щільність стаціонарного процесу.

Теорема Бахнера – Хінчена

Теорема Хінчена

- корел

- неспаднаф-ція обмеж. варіації

Доведення

- корел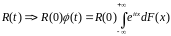

- спектральна функція

Якщо існує 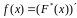- спектральна щільність

- корел. ф-я

9.Основні задачі математичної статистики:

1. Оцінка невідомих параметрів.

_{Нехай є} n-вимірна (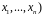 функція розподілу випадкової величини _{Параметр невідомий. Необхідно знайти найкращу оцінку .}

2. Перевірка статистичних гіпотез.

_{- основна гіпотеза}

_{- альтернативна}

_{Основні види:}

а) гіпотези про розподіл

_{б) гіпотези однорідності:}

_{Нехай є розподіли 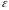та}

_{в) гіпотези незалежності:}

_{незалежні}

_{залежні.}

_{Основні позначення мат. статистики:}

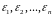_{Нехай є розподіл та його функція . Послідовність називається вибірка обсягу n з генеральної сукупності випадкової величини з функції розподілу}

_{-п.н.о.р.в.в. з}

_{В свою чергу, називається реалізацією вибірки, де - значення , - значення ,…, - значення .}

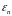_{Перепозначимо індекси:}

_{Таким чином утворимо реалізацію варіаційного статистичного ряду.}

_{- це є варіаційний статистичний ряд.}

_{- i-та порядкова статистика.}