Элементы теории вероятностей
1. В урне содержится A черных и B белых шаров. Случайным образом вынимают С шаров. Найти вероятность того, что среди них имеется:
(а) D белых шаров;
(б) хотя бы один белый шар.
-
Номер задания
1
2
3
4
5
6
7
8
9
10
A
5
6
6
7
4
8
6
4
5
7
B
6
5
5
4
5
6
7
7
6
4
C
5
4
5
4
4
5
4
4
7
3
D
3
2
3
2
2
3
4
2
3
2
Пример. В урне содержится 5 черных и 6 белых шаров. Случайным образом вынимают 4 шара. Найти вероятность того, что среди них имеется:
(а) 2 белых шара;
(б) хотя бы один белый шар.
Решение. Число всевозможных событий – все сочетания по 4 из 11 шаров:
где
обозначено число сочетаний
и
.
(а)
Событие A1
– среди вынутых шаров 2 белых, а таким
образом и 2 черных. Число таких событий
равно:
В результате по классическому
определению
вероятности имеем:
(б)
Событие A2
– среди вынутых шаров хотя
бы один
белый. Определим вероятность этого
события через вероятность противоположного
ему события
- среди вынутых
шаров нет ни одного белого:
Таким
образом, искомая вероятность равна:
2.
Три стрелка произвели по одному выстрелу
в одну и ту же мишень. Вероятность
попадания первым стрелком равна
вторым -
третьим -
Найти вероятность того, что мишень будет
поражена, если для этого достаточно
одного попадания.
-
Номер задания
1
2
3
4
5
6
7
8
9
10
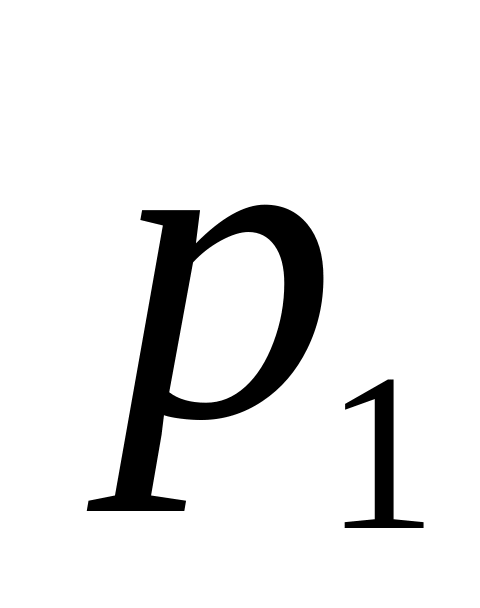
0.7
0.8
0.7
0.8
0.5
0.4
0.6
0.3
0.6
0.5
0.8
0.9
0.7
0.9
0.6
0.8
0.3
0.8
0.6
0.8
0.9
0.6
0.8
0.8
0.7
0.9
0.5
0.7
0.8
0.9
Пример. Информация отправлена от резидента в центр по трем различным каналам связи. Надежность каналов равна соответственно 60%, 90% и 50%. Найти вероятность того, что информация попадет в центр.
Решение.
Согласно условию задачи вероятность
передачи информации по каналам связи
равна
и
соответственно, в силу того, что:
.
Интересующее
нас событие А
- информация
попадает в центр, является противоположным
событию
-
информация не попадает в центр. Таким
образом, искомая вероятность события
А может
быть получена по формуле:
Учтем,
что
(события совместны и независимы), где
-символ
«произведения» событий, логически
соответствующий их одновременности
и событие
- информация по
-
каналу связи не
попала в центр.
Тогда,
учитывая теорему
о произведении вероятностей
совместных и независимых событий
,
а также тот факт, что
,
окончательно получаем:
3.
В первой урне имеются
белых и
черных шаров, во второй -
белых и
черных. Из первой урны во вторую наугад
перекладывают один шар. Затем шары во
второй урне перемешивают и наугад
извлекают два шара. Найти вероятность
того, что извлечены шары разного цвета.
-
Номер задания
1
2
3
4
5
6
7
8
9
10
3
1
2
3
4
4
5
2
3
6
2
3
3
1
2
3
2
4
5
2
6
2
3
5
5
6
3
3
2
5
2
3
4
2
1
1
4
5
6
3
Пример. В первой урне имеются 2 белых и 2 черных шаров, во второй - 4 белых и 2 черных. Из первой урны наугад берут два шара и перекладывают их во вторую урну. Цвет изъятых шаров неизвестен. Затем шары во второй урне перемешивают и наугад извлекают один шар. Найти вероятность того, что он белый.
Решение. Определим полную группу (попарно несовместных) событий (гипотезы):
-
из 1 урны во 2 переложили 2 белых шара,
-
из 1 урны во 2 переложили 2 черных шара,
-
из 1 урны во 2 переложили 1 белый и 1 черный
шар.
Воспользуемся формулой полной вероятности:
,
где
изучаемое нами событие
-
из 2 урны извлекли белый
шар.
Находим вероятности гипотез:
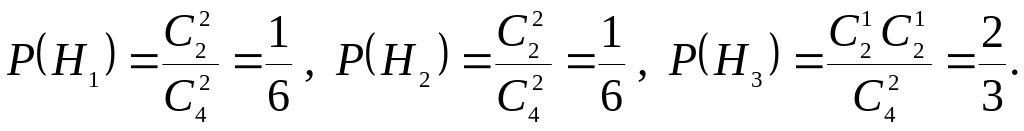
Находим условные вероятности события при данных гипотезах:
Тогда окончательно получаем:
4.
Непрерывная случайная величина
задана функцией распределения плотности
вероятности:
Найти
функцию распределения вероятности
,
математическое ожидание
и дисперсию
случайной величины
.
-
Номер задания
1
2
3
4
5
6
7
8
9
10
0.5
4.5
2
3
8
2.5
4
1.5
5
3.5
Пример.
Непрерывная случайная величина
задана функцией распределения плотности
вероятности
(см.
и требование
):
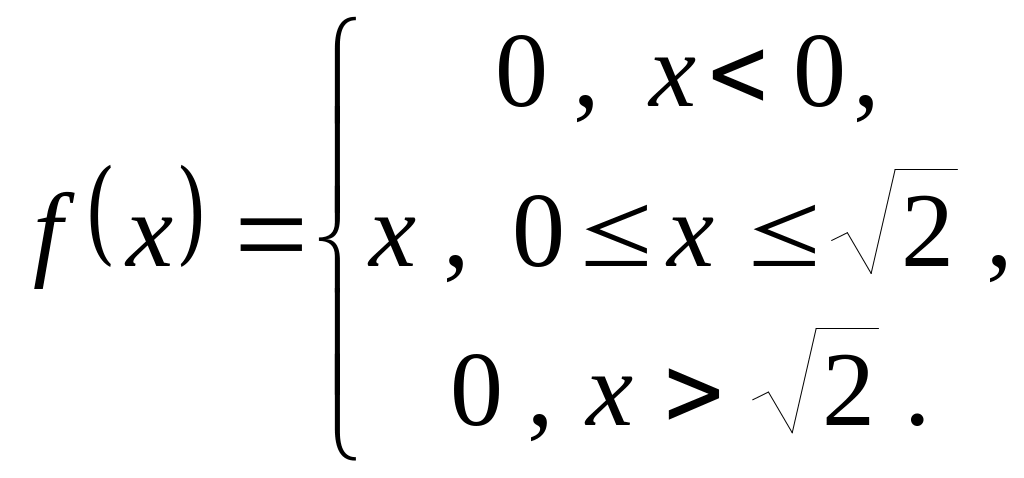
Найти , и .
Решение.
Функция
на отрезке
имеет вид (см.
):
.
Таким образом, для всей действительной оси получаем:
Математическое ожидание и дисперсию находим по формулам:
Замечание. Вычисление дисперсии можно технически упростить:
