Элементы математического анализа. Часть 2
1. Найти общее решение дифференциального уравнения:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
Пример. Найти общее решение дифференциального уравнения:
,
Решение.
Перед нами обыкновенное линейное
неоднородное
дифференциальное уравнение 1-го порядка
,
где
,
.
Тогда, выполняя подстановку (метод
Бернулли)
,
получаем систему уравнений для определения
новых неизвестных функций
и
:
Находим частное решение первого уравнения системы:
.
Подставляя
найденную функцию во второе уравнение
системы, для функции
получаем общее
решение:
,
где
– неопределенная константа интегрирования.
В результате, искомое общее
решение
исходного уравнения в явной
форме имеет
вид:
,
Проверка:
.
2. Найти общее решение дифференциального уравнения:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
Пример. Найти общее решение дифференциального уравнения:
Решение.
Соответствующее заданному характеристическое
уравнение
имеет два комплексно-сопряженных корня
,
где
и
Следовательно, согласно методу построения
общего
решения обыкновенного линейного
однородного
дифференциального уравнения 2-го порядка
с постоянными коэффициентами
(у
нас
),
получаем в явной
форме:
где
неопределенные константы интегрирования.
Полученное
решение может быть записано более
компактно - в виде одной
(модулированной
множителем
и с начальной
фазой
)
синусоиды:
Проверка: При получаем тождество
3. Используя теорему Даламбера исследовать числовой ряд на сходимость:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
Замечание. Выполняются равенства:
и
для любых
чисел
Пример. Используя теорему Даламбера исследовать числовой ряд на сходимость:
Решение.
Воспользуемся теоремой
(признаком)
Даламбера
для знакоположительного (для каждого
выполняется
)
числового ряда
:
В
силу того, что
,
заданный числовой ряд сходится
(имеет конечную
сумму, значение которой теоремой
Даламбера не
определяется).
4. Найти область сходимости степенного ряда:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
Пример. Найти область сходимости степенного ряда:
Решение.
- радиус
сходимости
степенного ряда
в силу теоремы
Абеля
определен неравенством:
где
(признак Даламбера) и в нашем случае
Тогда
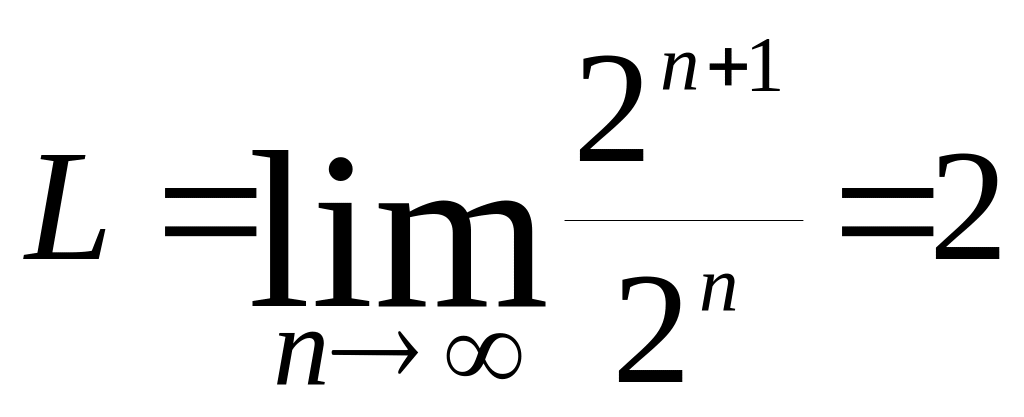и
Решаем последнее неравенство:
В
граничных точках
и
заданный степенной ряд расходится. В
самом деле, например, при
имеем:
Таким
образом, для области
сходимости
исходного степенного ряда получаем
окончательно открытый
интервал:
Проверка:
Например, при значении
из области сходимости получаем сходящийся
знакоположительный
числовой ряд
.
Контрольная работа 4