1. Логика высказываний

1. Основные определения

Язык логики высказываний - это формальный язык, в терминах которого мы формализуем те части повседневной речи, которые необходимы для представления логических и математических понятий.

Каждый формальный язык задается:

алфавитом, содержащим все символы языка,

синтаксисом, определяющим каким образом из символов языка формируются высказывания,

семантикой, при помощи которой интерпретируются элементы языка путем приписывания значений символам алфавита.

Алфавит логики высказываний состоит:

1. Из пропозициональных символов: .

2. Логических связок: .

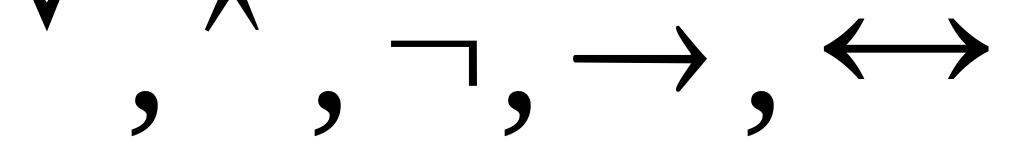3. Запятой и скобок.

Логические связки интуитивно соответствуют частицам и союзам, которые мы используем в повседневной жизни:

- конъюнкция (логическое “и”),

- дизъюнкция (логическое “или”),

- импликация (логическое “если …, то”),

- эквивалентность (логическое “тогда и только тогда, когда”),

- отрицание (логическое “не”).

Произвольная последовательность символов, принадлежащих алфавиту языка, называется выражением.

1. Пропозициональные символы являются высказываниями и называются атомарными высказываниями или атомами.

2. Если и - высказывания, то выражения , , , , также являются высказываниями, называемыми составными высказываниями.

3. Выражения, построенные в соответствии с пунктами 1 и 2, и только они являются высказываниями.

Высказывания логики высказываний также называются формулами.

Семантика логики высказываний интерпретирует высказывания, т. е. определяет при каких условиях высказывания являются истинными, а при каких ложными.

В логике высказываний существует два типа логических значений: - true – истина, - false – ложь.

Означиванием называется произвольная функция , где - множество атомов языка.

Пусть - множество высказываний языка. Истинностным означиванием или булевым означиванием называется такая функция , что для произвольных высказываний и верно:

1. Если - атом, то .

2. .

3. .

4. .

5. .

6. .

Теорема. Для каждого означивания существует и единственно истинностное означивание , являющееся расширением .

1.2. Таблицы истинности

Таблица истинности - это таблица, в которой собраны все возможные означивания атомов и соответствующих им расширений до высказывания. Таблицы истинности служат для определения истинности высказывания: является ли высказывание тавтологией, противоречием или оно выполнимо. Таблица истинности высказывания, содержащего - атомов, состоит из строк.

Таблицы истинности логических связок.

Высказывания логики высказываний можно классифицировать в соответствии с истинностью значений, которые они принимают.

Высказывание называется логически истинным или тавтологией, если для каждого истинностного означивания , верно что .

Высказывание называется логически ложным или противоречием, если для каждого истинностного означивания , верно что .

Высказывание называется выполнимым или подтвержденным, если существует такое истинностное означивание , что верно .

Два высказывания и называются логически эквивалентными, если для любого истинностного означивания справедливо .

Множество логических связок называется полным, если для любого высказывания логики высказываний существует логически эквивалентное ему высказывание, содержащее только связки из .

Теорема. Множество связок - является полным.

Следствие. Множества связок и - является полными (алгоритмы нахождения ДНФ и КНФ).

Пусть - множество высказываний. Высказывание называется логическим следствием из , если для любого истинностного означивания , обладающего свойством: , , можно заключить, что .

Множество высказываний называется семантически непротиворечивым, если существует истинностное означивание, которое подтверждает каждое высказывание из .

Множество высказываний называется семантически противоречивым, если существует истинностное означивание, которое не подтверждает хотя бы одно высказывание из .

Высказывание, подтверждающее множество высказываний , называется интерпретацией.

Наиболее часто используемые тавтологии:

1. - законы де Моргана.

2.

3. - закон двойного отрицания.

4. - закон контрапозиции.

5. - первый закон силлогистики.

7. - второй закон силлогистики.

8. - закон транспозиции

9. - закон исключения третьего.