1. Строительной механикой, в широком смысле, называется наука о методах расчета сооружений на прочность, жесткость и устойчивость. Самостоятельно как наука строительная механика начала развиваться в первой половине XIX века в связи с начавшимся активным строительством мостов, железных дорог, плотин, судов и крупных промышленных сооружений. Отсутствие методов расчета таких сооружений не позволяло осуществить легкие, экономичные и одновременно надежные конструкции. Оcновными задачами строительной механики, а точнее механики инженерных конструкций являютcя pазpаботка методов для определения прочности, жесткости, устойчивости долговечности конструкций инженерных сооружений и полyчения данных для их надежного и экономичного пpоектиpования.

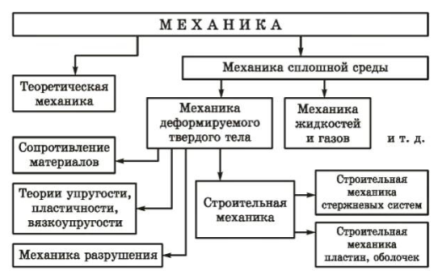
Направление развития:

С одной стороны, по пути уточнения расчетных схем и исходных гипотез, положенных в основу расчета, с другой - по пути разработки все более совершенных методов расчета, ориентированных на применение компьютера.

2. Нагрузки и воздействия. Нагрузки по способу действия: однократн.(все сост. сис-мы сил одновременно увелис-ся от 0 до опр-го знач.), повторно-перемен.(когда каждая сост-щая может изм-ся по своей величине в опр. пределах независимо от других сил), подвижн.(может передвигаться и занимать различные полож.на опр. части констр.) , неподвижн.(сохр. неизмен. полож-е длительное время). В зависимости от хар-ра изм-я во времени – статич. и динамич. нагр. При действии статич. нагр. колебания сооруж. Либо совсем не появляются, либо они незначительны. При статич. нагр. упругой сис-мы в любой момент времени всегда имеет место равновесие между внутр. и внешн. силами. Динамическая – нагр. при кот. сооруж. и его эл-ты получают ускорения. При действии динамич. нагр. необх. учитывать силы инерции как самой сис-мы, так и расположенного на ней оборуд-я.

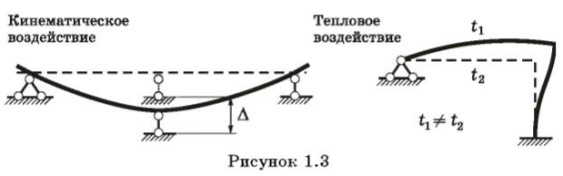
Воздействия. Температура, осадка фунд., землетрясение, действ. огня, хим. агрессия, коррозия и т.д.

3 Классифик. Стержневых систем

- По виду соединения стержней- с шарнирным соединением

(фермы, решетчатые башни, купола, оболочки, структуры); с

Жесткими соединением ( рамы).

- по схеме нагружения – плоские, воспринимающие внешние

Нагрузки, действ. Только в плоскости стержневой системы, простран-

Ственные, воспринимающие внешние нагрузки произвольного

Направления.

- по степени статической определимости, статически неопредел.

- по назначению- опорные, пролетные, совмещенные.

4 Связи и их характеристики

- шарнирно-пожвижн. Опора. Рис.

- Шарнирно- неподвижн.опора. рис.

- простой шарнир ( он соед. 2 элементами) рис.

Сложный или ( кратный) шарнир рис.

- жесткая заделка рис.

-скользящая заделка рис.

7. Строительная механика рассматривает геометрически неизменяемые системы (сооружения), то есть такие, перемещения точек которых возможны только в результате деформации системы

Геометрическая неизменяемость Стержневая система, которая не может иметь перемещений без деформаций, называется

геометрически неизменяемой. Иными словами,геометрически неизменяемая система не может иметь перемещений, если материал её стержней является абсолютно жёстким.Строительные конструкции должны быть геометрически неизменяемыми. Геометрически изменяемые системы называются механизмами

Фрагмент стержневой системы, расстояние между любыми двумя точками которого может изменяться только за счёт деформаций,

называется жёстким диском (рис.4.1). Иными словами, взаимные перемещения точек жёсткого диска невозможны, если его материал является абсолютно жёстким. Примерами жёстких дисков являются фрагмент стержневой системы, не содержащий шарниров,и шарнирный треугольник

Д и с к – часть системы (один или несколько соединённых друг с другом элементов), форма и размеры которой могут изменяться только вследствие деформации материала.

Примеры дисков:

1)диски из одного элемента

2)  диски из нескольких элементов

Незакреплённый диск может перемещаться в плоскости или пространстве, при этом координаты его точек в общей (глобальной) системе координат xyz изменяются , но в собственных (локальных) координатных осях x_D y_D z_D , связанных с самим диском, положение его точек остается неизменным, если считать элементы диска недеформируемыми, – это означает, что диск перемещается как жёсткое целое.

Классификация связей по кинематическому признаку

Н е о б х о д и м ы е   с в я з и – это связи, удаление  которых вызывает изменение кинематической природы системы (геометрически неизменяемая система превращается в геометрически изменяемую или мгновенно изменяемую, мгновенно изменяемая система становится геометрически изменяемой).

 Л и ш н и м и  называются связи, при удалении которых кинематическая природа системы не изменяется, но эти связи ограничивают  перемещения  в   деформируемой  системе.

 Л о ж н ы е   с в я з и – такие, которые не оказывают никакого влияния ни на кинематическую природу системы, ни на перемещения в ней, определяемые с учётом деформации элементов.

 Иными словами, при удалении ложной связи в системе  ничего не изменяется – ни в случае учёта деформаций её элементов, ни в предположении об условной идеальной жёсткости материала.

Лишние и ложные связи с количественной точки зрения являются избыточными, так как они не нужны для обеспечения геометрической неизменяемости системы – для этого достаточно только необходимых связей. Несмотря на своё название, лишние связи, тем не менее, нужны для реализации определённых эксплуатационных качеств сооружения и появляются в расчётной схеме как результат принятия тех или иных инженерных решений при проектировании конструкций. Более того, в действительности систем без лишних связей не бывает – они возникают лишь в результате формирования расчётных моделей сооружений с идеализацией их реальных свойств (в частности, если пренебрегать трением в шарнирах, опорах и т.п.).

А вот ложные связи не нужны вообще, их можно рассматривать как «паразитные»; они должны быть выявлены и удалены из системы до начала её расчёта – в противном случае математическое решение задачи определения усилий и перемещений в сооружении 

11.Необходимое аналитическое условие геометрической неизменяемости. Как было показано выше, у геометрически не­изменяемой системы имеется достаточное количество связей, ко­торые при правильной расстановке обеспечивают ее неподвиж­ность. Такая конструкция не должна обладать «свободой», т. е. необходимо, чтобы ее число степеней свободы было не большим нуля. Следовательно, необходимое аналитическое условие гео­метрической неизменяемости системы имеет вид W<0.

Однако выполнение условия (1.6) еще не гарантирует геомет­рической неизменяемости системы. Это необходимый, но не дос­таточный признак, так как ничего не известно о правильности расположения связей.

Общий аналитический метод. Общим методом исследо­вания неизменяемости сооружения является анализ определителя системы уравнений для всех усилий в элементах конструкции при действии произвольной нагрузки.