Литература необходимая для проведения работы:
П. Т. Апанасов, М. И. Орлов. Сборник задач по математике. - М., ВШ,1987.
И. Л. Зайцев. Элементы высшей математики. -М., Наука,1972.
И.А. Соловейчик, В.Т. Лисичкин. Математика .-М., ВШ, 1991.
Практическая работа № 8
Тема: Решение задач прикладного характера с применением определенного интеграла.
Вариант-1.
1. Вычислить работу, совершенную при сжатии пружины на 0,02 м, если для сжатия ее на 0,04 м нужно приложить силу в 2 Н .
2. Скорость точки, движущейся прямолинейно, задана уравнением v=3t²2t1,м/c. Вычислить путь, пройденный точкой за 5 секунд после начала движения.
3.Найти площадь фигуры, ограниченной кривыми, заданными уравнениями:
y=2xx²; y=0.
Практическая работа №8
Тема: Решение задач прикладного характера с применением определенного интеграла.
Вариант-2.
1.Вычислить работу, совершенную при сжатии пружины на 0,06 м, если для сжатия ее на 0,03 м нужно приложить силу 15 Н.
2.Скорость точки, движущейся прямолинейно, задана уравнением v=24t6t²¸ м/с. Вычислить путь, пройденный точкой от начала движения до ее остановки.
3.Найти площадь фигуры, ограниченный кривыми, заданными уравнениями:
y= x², y= 3x.
Практическая работа № 8
Тема: Решение задач прикладного характера с применением определенного интеграла
Вариант-3.
1. Вычислить работу, совершенную при сжатии пружины на 0,06 м, если для ее сжатия на 0,01 м нужно приложить силу в 10 Н.
2. Скорость точки, движущийся прямолинейно, задана уравнением
v=18t-6t² , cм/с. Вычислить путь , пройденный точкой от начала движения до остановки.
3. Найти площадь фигуры, ограниченной линиями:
y= -x²+6х-5 и y=0;
Практическая работа № 8
Тема: Решение задач прикладного характера с применением определенного интеграла
Вариант-4.
1. Найдите работу, которую необходимо затратить при сжатии пружины на 0,05 м, если сила в 4 Н требуется для ее сжатия на 0,1 м.
2. Скорость точки, движущейся прямолинейно, задана уравнением
v=6t²-4t-10, см /с. Вычислить путь, пройденный точкой за 4с от начала
движения.
3. Найти площадь фигуры, ограниченной линиями:
Практическая работа № 8
Тема: Решение задач прикладного характера с применением определенного интеграла
Вариант-5.
1. Вычислить работу, которую нужно затратить при сжатии пружины на 3 см, если сила в 2 Н сжимает эту пружину на 1 см.
2.
Скорость движения точки V = 9t
–
8t. Найти путь, пройденный точкой за
четвертую секунду.
3. Найти площадь фигуры, ограниченной линиями:
y= x²-2x+3 и y=x+3.
Практическая работа № 8
Тема: Решение задач прикладного характера с применением определенного интеграла
Вариант-6.
Вычислить работу, которую нужно затратить при растяжении пружины на 8 см, если сила в 3 Н растягивает пружину на 1 см.
Скорость движения тела задана уравнением V =
м/c.
Найти путь, пройденный телом за вторую
секунду.Найти площадь фигуры, ограниченной линиями:
y = x2 и y = 2 – x2.
Содержание практической работы
Задание 1. Найти площадь фигуры, ограниченной линиями.
1)
2)
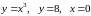
3)
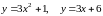
4)
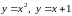
5)
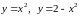
6)
Задание 2. Найти площадь фигуры, ограниченной линиями, заданными параметрически.
1)
2)
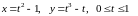
3)
4)
5)
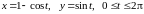
6)
Задание 3. Найти объем тела, полученного вращением вокруг оси OX фигуры, ограниченной линиями.
1)
2)
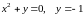
3)
4)
5)
6)
Практическая работа №9
Тема: Решение дифференциальных уравнений с разделяющимися переменными.
Цель занятия: закрепить навыки решения дифференциальных уравнений первого порядка с разделяющимися переменными.
Умения и навыки, которые должны приобрести обучающиеся на занятии: находить общее и частное решения дифференциального уравнения первого порядка и с разделяющимися переменными.
Наглядные пособия, оборудование: плакаты с формулами дифференцирования и интегрирования; микрокалькулятор; дидактические карточки с заданиями.