Повторение теоретических основ:

1. Что называется криволинейной трапецией?

2. Вычисление площади криволинейной трапеции.

3. Вычисление пути, пройденного телом при неравномерном движении, за промежуток времени от до , если задан закон движения тела .

4. Вычисление работы переменной силы 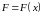, вызвавшей перемещение от до .

1. Криволинейная трапеция Пусть на отрезке [а; b] оси Ох задана непрерывная функция f, не меняющая на нем знака. Фигуру, ограниченную графиком этой функции, отрезком [а; b] и прямыми х = а и х = b (рис. 1), называют криволинейной трапецией.

Площадь криволинейной трапеции.

S=F(b)-F(a).

Алгоритм нахождения площади криволинейной трапеции

1. Построить графики линий.

2. Определить криволинейную трапецию.

3. Выделить функцию f , ограничивающую трапецию.

4. Определить отрезок [a; b] оси Ох.

5. Найти одну из первообразных функции f .

6. Используя формулу S=F(b)-F(a) , вычислить площадь.

Пример типового расчета:

Вычислить площадь криволинейной трапеции, ограниченной линиями

у = 4 - х² и у = 0

Решение:

1. Построим криволинейную трапецию:

у = 4 - х²- квадратичная функция, график – парабола, ветви направлены вниз. у = 0 - ось абсцисс.

2. Найдём [а;b]:

4-х² = 0; х² = 4 х = -2 или х = 2, т. е. а = -2 b = 2

3. Найдём площадь криволинейной трапеции по формуле: S = F(b) – F(а)

2. Вычисление пути, пройденного точкой

Путь, пройденный точкой при неравномерном движении по прямой с переменной скоростью за промежуток времени от до вычисляется по формуле .

Пример типового расчета:

1. Скорость движения точки м/с.

Найти путь, пройденный точкой за 4-ю секунду.

Решение: согласно условию, . Следовательно,

2. Два тела начали двигаться одновременно из одной точки в одном направлении по прямой. Первое тело движется со скоростью м/с, второе — со скоростью v = (4t+5) м/с. На каком расстоянии друг от друга они окажутся через 5 с?

Решение: очевидно, что искомая величина есть разность расстояний, пройденных первым и вторым телом за 5 с:

3. Тело брошено с поверхности земли вертикально вверх со скоростью и = (39,2—9,8^) м/с. Найти наибольшую высоту подъема тела.

Решение: тело достигнет наибольшей высоты подъема в такой момент времени t, когда v = 0, т.е. 39,2—9,8t = 0, откуда I = 4 с. По формуле (1) на ходим

3. Вычисление работы переменной силы , вызвавшей перемещение от до .

Работа, произведенная переменной силой f(х) при перемещении по оси Ох материальной точки от х = а до х=b, находится по формуле При решении задач на вычисление работы силы часто используется закон Г у к а: F=kx, (3) где F — сила Н; х—абсолютное удлинение пружины, м, вызванное силой F, а k —коэффициент пропорциональности, Н/м.

Пример типового расчета:

1. Пружина в спокойном состоянии имеет длину 0,2 м. Сила в 50 Н растягивает пружину на 0,01 м. Какую работу надо совершить, чтобы растянуть ее от 0,22 до 0,32 м?

Решение: используя равенство (3), имеем 50=0,01k, т. е. kК = 5000 Н/м. Находим пределы интегрирования: а = 0,22 — 0,2 = 0,02 (м), b=0,32— 0,2 = 0,12(м). Теперь по формуле (2) получим

Практика: студенты выполняют расчеты по выдаваемым дидактическим карточкам с заданиями – 6 вариантов.

Приложение: дидактические карточки с заданиями (6 вариантов).

Контрольные вопросы:

1. Что называется определенным интегралом?

2. Как вычисляется определенный интеграл?

3. Свойства определенного интеграла?

4. Что называется криволинейной трапецией?

5. Как с помощью интеграла найти площадь криволинейной трапеции; путь, пройденный телом при неравномерном движении; работу переменной силы F, вызвавшей перемещение от ?
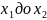