Повторение теоретических основ:

1. Определение неопределенного интеграла.

2. Свойства неопределенного интеграла.

3. Таблица основных формул интегрирования.

4. Непосредственное интегрирование. Приемы непосредственного интегрирования.

5. Метод подстановки при нахождении неопределенных интегралов.

6. Формула интегрирования по частям.

1. Функция F (x) называется первообразной для функции f (x) в промежутке a < x < b, если в любой точке этого промежутка ее производная равна f (x):

F’ (x) = ƒ (x) => dƒ (x) = ƒ (x) dx, a< x < b

Отыскание первообразной функции по заданной её производной f(x) или по дифференциалу ƒ (x) dx есть действие, обратное дифференцированию, - интегрирование.

Совокупность первообразных для функций f(x) или для дифференциала (x) dx называется неопределённым интегралом и обозначается символом S ƒ (x) dx. Таким образом,

S ƒ (x) dx= F(x)+C если d[ F(x)+C]= ƒ(x)dx

F(x)- подынтегральная функция;

F(x)dx- подынтегральное выражение;

С- произвольная постоянная.

2. Основные свойства неопределенного интеграла:

1. Неопределенный интеграл от дифференциала функции равен этой функции плюс произвольная постоянная:

.

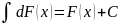2. Дифференциал неопределенного интеграла равен подынтегральному выражению, а производная неопределенного интеграла равна подынтегральной функции:

, .

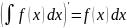3. Неопределенный интеграл алгебраической суммы функций равен алгебраической сумме неопределенных интегралов этих функций:

;

4. Постоянный множитель подынтегрального выражения можно выносить за знак неопределенного интеграла:

.

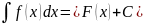5. Если и 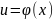– любая известная функция, имеющая непрерывную производную, то

.

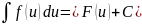3.Основные формулы интегрирования (таблица интегралов):

1. ;

2. , (n );

3. ;

4. ;

5. ;

6. 

7. 

8. 

9. 

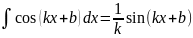
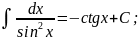
Методы интегрирования

Наиболее важными методами интегрирования являются: 1) метод непосредственного интегрирования (метод разложения), 2) метод подстановки (метод введения новой переменной), 3) метод интегрирования по частям.

1. Метод непосредственного интегрирования

Задача нахождения неопределенных интегралов от многих функций решается методом сведения их к одному из табличных интегралов.

Пример типового расчета:

Найти неопределенный интеграл: ∫cos(7x-3)dx

∫cos(7x-3) dx = ∫cos(7x-3)d(7x-3)= sin(7x-3)+C

2. Метод подстановки (интегрирование заменой переменной)

Алгоритм вычисления неопределенного интеграла методом подстановки:

1. Определяют, к какому табличному интегралу приводится данный интеграл (предварительно преобразовав подынтегральное выражение, если нужно).

2. Определяют, какую часть подынтегральной функции заменить новой переменной, и записывают эту замену.

3. Находят дифференциалы обеих частей записи и выражают дифференциал старой переменной (или выражение, содержащее этот дифференциал) через дифференциал новой переменной.

4. Производят замену под интегралом.

5. Находят полученный интеграл.

6. В результате производят обратную замену, т.е. переходят к старой переменной. Результат полезно проверять дифференцированием.

Пример типового расчета:

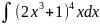
Введем подстановку:

 

Дифференцируя это равенство, имеем:  

Выразив отсюда 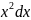, получим: . Подставив в данный интеграл вместо 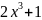и их выражения, получим:

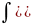)⁴ .