Содержание практической работы
Задание 1. Найти производные 1-го порядка данных функций
1)
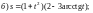
2)
3)
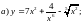
4)
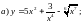
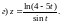
5)
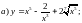
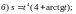
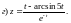
6)
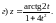
Задание 2. Составить уравнение касательной и нормали к кривой y=f(x) в точке с абсциссой х0.
1)
2)
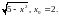
3)
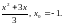
4)
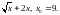
5)
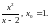
6)
Задание
3.
Найти производную
функции y=у(x),
заданной параметрически:
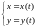
1)
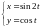
2)
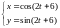
3)
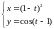
4)
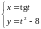
5)
6)
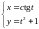
Задание 4. Найти дифференциалы функций:
1)
2)
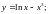
3)
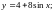
4)
5)
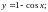
6)
Задание 5. Найти производную второго порядка функции y=f(x).
1)
2)
3)
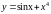
4)
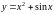
5)
6)
Задание 6. Найти производную функции логарифмическим дифференцированием
1)
2)
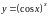
3)
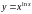
4)
5)
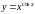
6)
Задание 7. Найти пределы, используя правило Лопиталя.
1)
2)
3)
4)
5)
6)
Практическая работа №4
Тема: Дифференцирование сложных функций.
Цель: сформировать умение находить производные функций, заданных в явном, логарифмическом и параметрическом виде.
Теоретические сведения к практической работе
Правила дифференцирования
VI Производная сложной функции
Производной n-го порядка называется производная от производной (n–1)-го порядка. Производные высших порядков вычисляются последовательным дифференцированием данной функции.
Производная
второго порядка
или
Производная третьего порядка или и т. д.
Пример 1. Найти производные функций:
а)
Решение.
Сложная степенная функция, независимая переменная есть v, т. е. v=1; используя формулу (3), получим:
Пример 5. Найти производную второго порядка функции
Решение. поэтому найдём производную первого порядка, а затем второго.
Содержание практической работы
Задание 1. Найти производные 1-го порядка данных функций
1)
2) 3)
4)
5)
6)
Задание 2. Составить уравнение касательной и нормали к кривой y=f(x) в точке с абсциссой х0.
1)
2)
3)
4)
5)
6)
6)
Задание 5. Найти производную второго порядка функции y=f(x).
1)
2)
3)
4)
5)
6)
Задание 6. Найти производную функции логарифмическим дифференцированием
1)
2)
3)
4)
5)
6)
Задание 7. Найти пределы, используя правило Лопиталя.
1)
2)
3)
4)
5)
6)
Практическая работа №5
Тема: Исследование функции с помощью производной и построение графика.
Практическая работа №6
Тема: Вычисление неопределенных интегралов.
Цель занятия: обобщить и систематизировать знания студентов при изучении основных формул интегрирования; продолжать формировать умения и навыки применения интегрирования функций; закрепить приемы и способы вычисления неопределенных интегралов, используя таблицу; развивать навыки сравнения при решении неопределенных интегралов одним из способов вычисления; воспитывать такие качества характера, как настойчивость в достижении цели.
Умения и навыки, которые должны приобрести обучаемые на занятии: в результате овладения содержанием раздела «неопределенные интегралы» студенты должны знать: определение понятия «неопределенный интеграл»; свойства неопределенного интеграла; методы вычисления неопределенного интеграла; уметь: применять известные методы вычисления неопределенных интегралов;
Наглядные пособия, оборудование: плакат с таблицей интегралов; плакат с основными свойствами интегрирования; дидактические карточки с заданиями (4 варианта)