
- •1. Оценить погрешность, если аргументы функции имеют 4 верных знака. Определить, с каким числом верных знаков следует взять аргументы, чтобы значение функции имело три значащих цифры:
- •Решение:
- •2. Пусть , . Решить задачу минимизации квадратичной функции методом наискорейшего спуска. Построить линии уровня с указанием векторов спуска. Найти точное и приближенное решение слау .
- •Решение:
- •3. Для функции, заданной таблицей
- •Решение:
- •4. С точностью до 0,0005 вычислить наименьший по модулю корень уравнения:
- •Решение
- •Уточним корень методом половинного деления:
- •Уточним корень методом половинного деления:
- •5. Приняв шаг , вычислить интеграл . Оценить погрешность результата по правилу Рунге (методом двойного пересчета).
- •Решение:
- •6. Для функции, заданной таблицей
- •Решение:
- •Решение:
1. Оценить погрешность, если аргументы функции имеют 4 верных знака. Определить, с каким числом верных знаков следует взять аргументы, чтобы значение функции имело три значащих цифры:
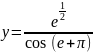
Решение:
Оценим погрешность, если аргументы функции имеют 4 верных знака.
Пусть:


Возьмем их значения с четырьмя верными знаками:



Вычислим приближенное значение функции:

Согласно формуле

где




и, следовательно,

Значит результат имеет четыре верных знака.
Определим, с каким числом верных знаков следует взять аргументы, чтобы значение функции имело три значащих цифры.
Определим приближенные значения функции и ее частных производных:





Абсолютная
погрешность
 удовлетворяет условию:
удовлетворяет условию:

Используя предположение о равенстве абсолютных погрешностей аргументов:

Таким образом, каждый из приближенных аргументов следует взять с четырьмя верными знаками.
2. Пусть , . Решить задачу минимизации квадратичной функции методом наискорейшего спуска. Построить линии уровня с указанием векторов спуска. Найти точное и приближенное решение слау .
Решение:
В
качестве начального приближения примем
 .
.
Критерий окончания итераций:

Вычислим градиент направления спуска:





Другие итерации в таблице:
k |
|
|
|
|
|
|
||||||
0 |
0 |
0 |
2 |
-6 |
0,4 |
0,8 |
-2,4 |
6,324555 |
1,6 |
|||
1 |
0,8 |
-2,4 |
-1,2 |
-0,4 |
2 |
-1,6 |
-3,2 |
1,264911 |
0,8 |
|||
2 |
-1,6 |
-3,2 |
0,4 |
-1,2 |
0,4 |
-1,44 |
-3,68 |
1,264911 |
0,32 |
|||
3 |
-1,44 |
-3,68 |
-0,24 |
-0,08 |
2 |
-1,92 |
-3,84 |
0,252982 |
0,16 |
|||
4 |
-1,92 |
-3,84 |
0,08 |
-0,24 |
0,4 |
-1,888 |
-3,936 |
0,252982 |
0,064 |
|||
5 |
-1,888 |
-3,936 |
-0,048 |
-0,016 |
2 |
-1,984 |
-3,968 |
0,050596 |
0,032 |
|||

3. Для функции, заданной таблицей
x |
-3 |
-2 |
-1 |
0 |
y |
0 |
2 |
-1 |
-4 |
построить
интерполяционный полином и вычислить
его значение при
 .
.
Решение:
Запишем систему уравнений на коэффициенты:


Откуда:




Значит
интерполяционный полином имеет вид:


Множители Лагранжа:






Для применения многочлена Ньютона сначала упорядочим узлы в порядке возрастания расстояния от точки x, получаем следующую последовательность узлов интерполяции:
 ,
,
 ,
,
 ,
,

Разделенные разности:
первого порядка:



второго порядка:


третьего порядка:

Таблица разделенных разностей:
-3 |
0 |
|
|
|
|
|
2 |
|
|
-2 |
2 |
|
-2,5 |
|
|
|
-3 |
|
5/6 |
-1 |
-1 |
|
0 |
|
|
|
-3 |
|
|
0 |
-4 |
|
|
|




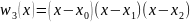


После раскрытия скобок:







