- •1. Предмет теоретической механики. Основные абстракции.
- •2. Предмет кинематики.
- •3. Способы задания движения точки
- •Связь между координатным и естественным способами задания движения точки
- •4. Определение скорости точки при векторном способе задания движения.
- •Скорость точки в данный момент времени
- •Ускорение точки при векторном способе задания движения
- •1. Определение скорости и ускорения точки при координатном способе задания движения
- •Определение скорости точки
- •2. Вращение твердого тела вокруг неподвижной оси.
- •2. Разложение плоскопараллельного движения на поступательное вместе с полюсом и вращательное вокруг полюса
- •Основные кинематические характеристики плоского движения
- •3. Определение скоростей точек тела
- •Следствие 2. Концы скоростей точек неизменяемого отрезка лежат на одной прямой и делят эту прямую на части пропорциональные расстояниям между соответствующими точками отрезка
- •4. План скоростей
2. Вращение твердого тела вокруг неподвижной оси.
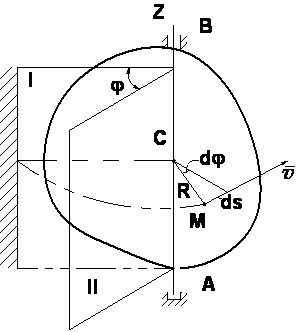
Вращательнымназывается такое движение твердого тела, при котором во все время движения какие-либо две точки тела остаются неподвижными (проходящая через эти неподвижные точки прямая называется осью вращения), а все остальные точки описывают траектории, представляющие собой окружности, плоскости которых перпендикулярны к оси вращения, а центры лежат на этой оси.
|
φ = f (t) (3. 3) |
|
|
|
|
|
|
|
Примеры:
Равномерное вращение (ω = const) |
Равнопеременное вращение (= const) |
d = dt =t = /t
|
|
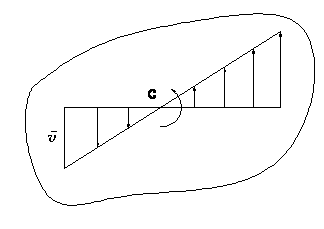
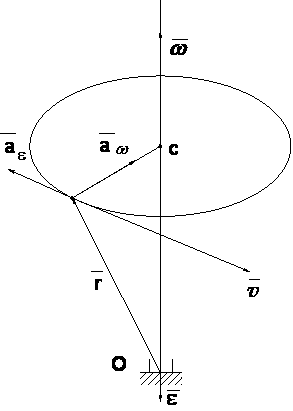
3. Скорости и ускорения точек вращающегося твердого тела
|
Вращательная скорость точки
v = R ω (3. 6)
|
Модуль вращательной скорости точки твердого тела равен произведению расстояния от точки до оси вращения на угловую скорость тела
Ускорение точки
или
|
4. Векторные выражения вращательной скорости, вращательного и центростремительного ускорений.
Формулы Эйлера.
|
|
|
- формулы Эйлера
|
Векторные выражения вращательного и центростремительного ускорения точки
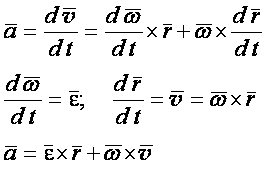
![]() - полное
ускорение точки
- полное
ускорение точки
![]() - вращательное
ускорение точки
- вращательное
ускорение точки
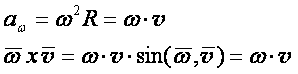
- центростремительное ускорение точки
|
|
1. Уравнения плоскопараллельного движения
Плоскопараллельным (или плоским) называется такое движение твердого тела, при котором все его точки перемешаются параллельно некоторой неподвижной плоскости П.
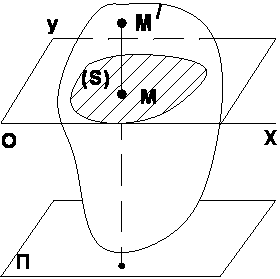
Рассмотрим сечение S тела какой-нибудь плоскостью Oxy, параллельной плоскости П. При плоскопараллельном движении все точки тела, лежащие на прямой ММ/, перпендикулярны к сечению (S), то есть к плоскости П движутся тождественно и в каждый момент времени имеют одинаковые скорости и ускорения. Поэтому для изучения движения всего тела достаточно изучить, как движется сечение S тела в плоскости Oxy.
|
|
Уравнения (4.1) определяют закон происходящего движения и называются уравнениями плоскопараллельного движения твердого тела.
2. Разложение плоскопараллельного движения на поступательное вместе с полюсом и вращательное вокруг полюса
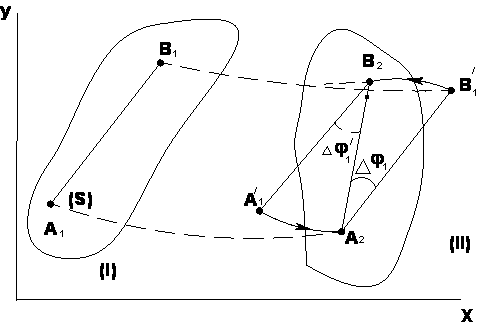
Покажем, что плоское движение слагается из поступательного и вращательного. Для этого рассмотрим два последовательных положения I и II, которые занимает сечение Sдвижущегося тела в моменты времени t1 иt2= t1 + Δt. Легко видеть, что сечение S, а с ним и все тело можно привести из положения I в положение II следующим образом: переместим сначала тело поступательно, так, чтобы полюс А, двигаясь вдоль своей траектории, пришел в положение А2. При этом отрезок A1B1займет положение , а затем повернем сечение вокруг полюса А2 на угол Δφ1.
|
Следовательно, плоскопараллельное движение твердого тела слагается из поступательного движения, при котором все точки тела движутся так же как полюс А и из вращательного движения вокруг этого полюса.
При этом следует отметить, что вращательное движение тела происходит вокруг оси, перпендикулярной к плоскости П и проходящей через полюс А. Однако для краткости мы будем в дальнейшем называть это движение просто вращением вокруг полюса А.
Поступательная часть плоскопараллельного движения описывается, очевидно, первыми двумя из уравнений (2. 1), а вращение вокруг полюса А - третьим из уравнений (2. 1).

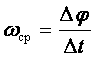
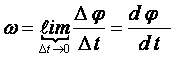 или
или 
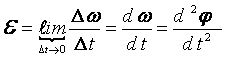 или
или
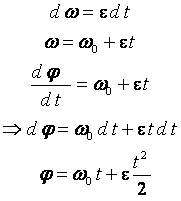
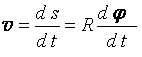
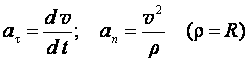

 (3.8)
– центростремительное
ускорение
(3.8)
– центростремительное
ускорение 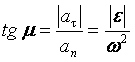 (3.10)
(3.10)
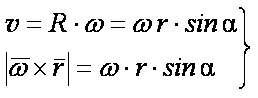
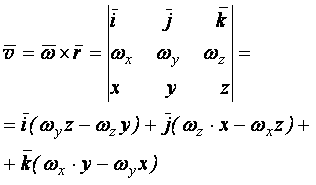
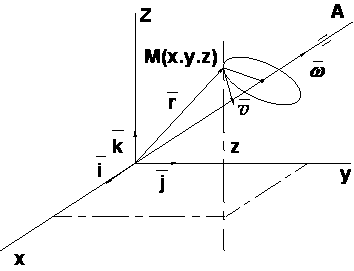
 (3.12)
(3.12)

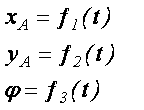 (4.1)
(4.1)