Лабораторная работа №3

Оценивание точности измерений на базе теории погрешностей Общие положения

Согласно РМГ 29-99 точность результата измерений (точность измерений) - одна из характеристик качества измерения, отражающая близость к нулю погрешности результата измерения (считают, что чем меньше погрешность измерения, тем больше его точность).

Согласно точность измерения - близость согласования между измеренным значением величины и истинным значением измеряемой величины.

Примечание 1 к VIM. Понятие «точность измерения» не является величиной и не задается численным значением величины. Говорят, что измерение является более точным, когда оно предполагает меньшую погрешность измерения.

Примечание 3 к VIM. Под «точностью измерения» иногда понимают близость согласования между измеренными значениями величины, которые приписываются измеряемой величине.

Для оценивания точности измерения можно использовать аппарат теории погрешностей и концепции неопределенностей.

Теория погрешностей дает рекомендации, касающиеся оценивания точности измерений, которые представлены в ГОСТ 8.207 и МИ 1552.

Неисключенная систематическая погрешность – составляющая погрешности результата измерений, обусловленная погрешностями вычисления и введения поправок на влияние систематических погрешностей или систематической погрешностью, поправка на действие которой не введена вследствие ее малости (иногда этот вид погрешности называют неисключенный остаток систематической погрешности).

Неисключенная систематическая погрешность результата образуется из составляющих, в качестве которых могут быть неисключенные методические систематические погрешности, погрешности средств измерений и погрешности от других источников.

Согласно МИ 1552 за результат однократного измерения принимают значение величины, полученное при отдельном измерении. Составляющие погрешности результата измерения должны быть известны до проведения измерений. Предполагается, что составляющие погрешности результата измерения известны, случайные погрешности составляющих распределены нормально, известные систематические погрешности исключены, а неисключенные систематические погрешности, представленные заданными границами  , распределены равномерно.

Согласно ГОСТ 8.207 за результат Ã многократных наблюдений принимают их среднее арифметическое (точечную оценку).

à = (Σ x_i.) /n

^{i =1}

где х_i – i-й результат наблюдения;

n – число результатов наблюдений;

Затем возможно выполнение двух промежуточных операций для проверки правильности расчетов Ã.

1) Расчет отклонений V_i результатов наблюдений от среднего арифметического значения:

V_i = Ã – x_i

2) Расчет суммы отклонений (отклонения суммируют с учетом знаков):

_n

Σ V_i. ≈ 0

^{i =1}

Если сумма отклонений практически равна нулю, расчеты значений Ã и V_i можно считать правильными, в противном случае необходимо перепроверить расчеты.

Расчет оценки с к о результатов наблюдений:

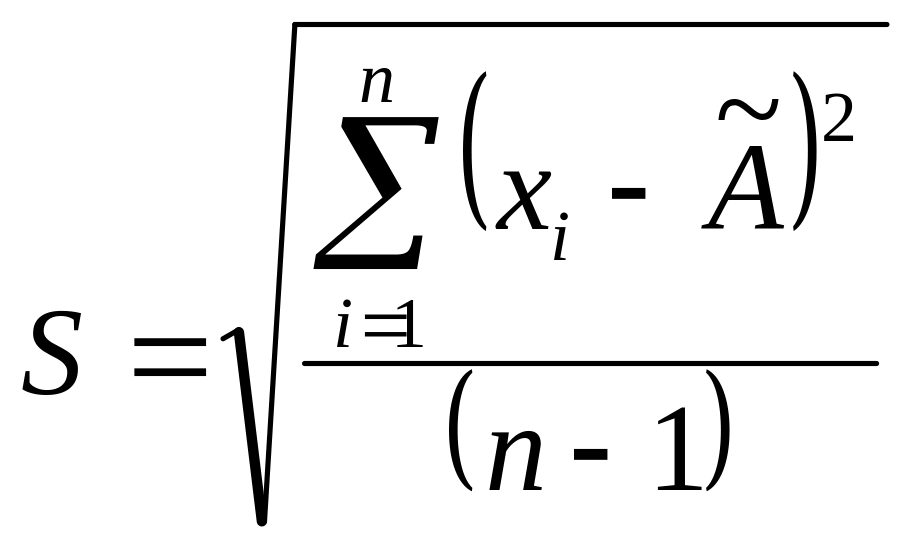
Оценку среднего квадратического отклонения результата измерения (оценку с к о среднего арифметического значения) определяют из зависимости

,

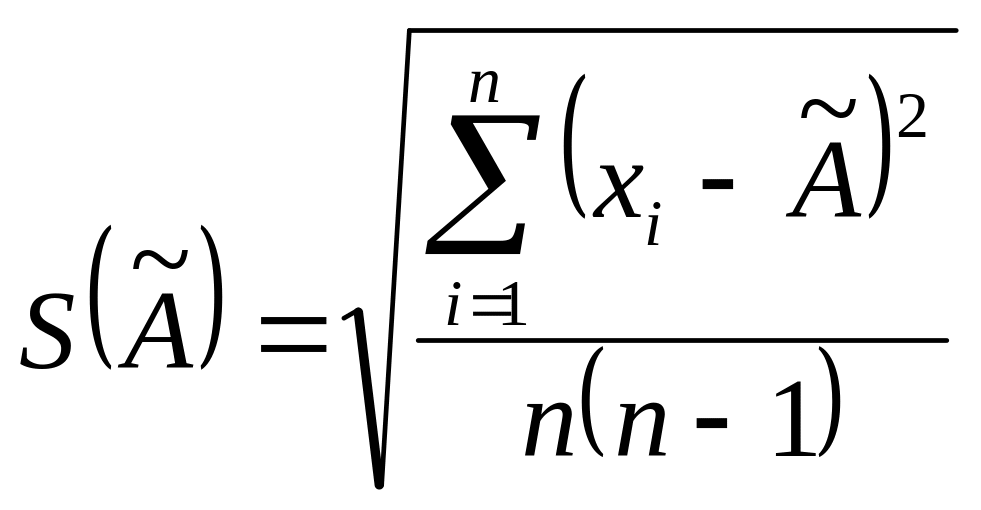При наличии ранее рассчитанного значения S можно воспользоваться той же зависимостью, представленной в виде

___

S(Ã) = S /√ n

Доверительные границы (без учета знака) случайной погрешности ε результата измерения рассчитывают из зависимости

,

где t – коэффициент Стьюдента, зависящий от доверительной вероятности Р и числа результатов наблюдений n (находят из таблицы 1, взятой из справочного приложения 2 ГОСТ 8.207). В случае отсутствия значимых неисключенных систематических составляющих погрешности за значения границ погрешности результата измерения Δ принимают полученное значение ε.

Таблица 1 – Значение коэффициента t для случайной величины Y, имеющей распределение Стьюдента с n-1 степенями свободы

n-1	Р=0,95	Р=0,99	n-1	Р=0,95	Р=0,99
3	3,182	5,841	16	2,120	2,921
4	2,776	4,604	18	2,101	2,878
5	2,571	4,032	20	2,086	2,845
6	2,447	3,707	22	2,074	2,819
7	2,365	3,499	24	2,064	2,797
8	2,306	3,355	26	2,056	2,779
9	2,262	3,250	28	2,048	2,763
10	2,228	3,169	30	2,043	2,750
12	2,179	3,055	∞	1,960	2,576
14	2,145	2,977

Обычно принимают Р = 0,95 или (в особых случаях) 0,99 и выше. Особые случаи – те, в которых результаты измерений связаны со здоровьем и безопасностью жизни людей, с возможными значительными экономическими потерями. Иногда принимают Р = 0,99 если существенно затруднены возможности повторения измерительного эксперимента или имеются иные причины.

При числе степеней свободы более 30, что приравнивается к бесконечности, чаще всего используют округленные значения коэффициента t, принимая t ≈ 2 при Р = 0,95 и t ≈ 2,6 при Р = 0,99, а при вероятности свыше 0,99 для простоты принимают t ≈ 3.

Далее при наличии известных оценок частных неисключенных систематических составляющих погрешностей Θ_i рассчитывают границы неисключенной систематической составляющей погрешности. В качестве границ частных неисключенных систематических погрешностей принимают, например, пределы допускаемых погрешностей используемых мер (гирь, концевых мер длины) и/или других средств измерений, если эти погрешности представлены в их паспортах или иных документах. При использовании аттестованных средств измерений, если в результаты измерений вносится взятая из аттестата поправка, границей частной неисключенной систематической погрешности считают предельную погрешность аттестации.

Суммирование составляющих неисключенной систематической погрешности результата осуществляют на основе допущения о том, что все неисключенные систематические погрешности можно рассматривать как случайные величины. При отсутствии данных о виде распределений этих величин, их распределения принимают за равновероятные. Такое распределение приписывают погрешностям, поскольку его можно считать наихудшим из возможных вариантов.

Доверительные границы неисключенной систематической погрешности результата измерения вычисляют следующим образом. При наличии нескольких неисключенных систематических погрешностей, заданных своими границами i, доверительную границу неисключенной систематической погрешности результата измерения (Р) (без учета знака) вычисляют по формуле

,

где Θ_i – граница i-й неисключенной систематической погрешности;

k – поправочный коэффициент, определяемый принятой доверительной вероятностью и числом m составляющих Θ_i.

При Р = 0,90 k = 0,95; при Р = 0,95 k = 1,1.

Значение доверительной вероятности для вычисления границ неисключенной систематической погрешности принимают таким же, как и при вычислении доверительных границ случайной погрешности результата измерения.

При доверительной вероятности Р = 0,99 коэффициент k принимают равным 1,4, если число суммируемых неисключенных систематических погрешностей более четырех (m > 4). Если число суммируемых погрешностей равно четырем или менее четырех (m ≤ 4), то коэффициент k определяют по графику (рисунок 1) зависимостей k = f (m, l), представленному в стандарте ГОСТ 8.207.

Значение аргумента l рассчитывают по формуле

,

где Θ₁ – составляющая, наиболее отличающаяся от других числовым значением,

Θ₂ – составляющая, ближайшая к Θ₁.

Д

Рисунок 1 – Графики зависимостей k =f (m, l):

кривая 1 для m = 2; кривая 2 для m = 3 и кривая 3 для m = 4

алее для оценки значимости неисключенных систематических погрешностей по сравнению со случайными берут соотношение Θ/S(Ã).

Неисключенные систематические погрешности считают пренебрежимо малыми по сравнению со случайной составляющей если их значение менее 0,8 S(Ã). В таком случае принимают, что граница погрешности результата измерения Δ = ε.

Если значение неисключенной систематической погрешности превышает 8,0 S(Ã), то пренебрегают случайной погрешностью как пренебрежимо малой по сравнению с систематической и принимают, что граница погрешности результата Δ = Θ.

Если отношение неисключенной систематической составляющей погрешности к случайной находится между двумя указанными пределами, т.е.

0,8 ≤ Θ/S(Ã) ≤ 8,0,

то границу погрешности результата измерения находят путем построения композиции распределений случайных и неисключенных систематических погрешностей. В таком случае допускается границы погрешности результата измерения Δ (без учета знака) вычислять с использованием зависимости

,

где K – коэффициент, зависящий от соотношения случайной и неисключенной систематической погрешностей;

S_Σ – оценка суммарного среднего квадратического отклонения результата измерения.

Коэффициент K вычисляют по эмпирической формуле

.

Оценку суммарного среднего квадратического отклонения результата измерения определяют из зависимости

,

где Θ_i/√3 – оценка среднего квадратического отклонения i-й неисключенной систематической погрешности, полученная на основе ранее представленного допущения о равновероятном распределении этих погрешностей в границах ±Θ_i, а соответственно Θ_i²/3 – дисперсия этого отклонения.