5. Розрахунок і моделювання системи автоматичного регулювання

5.1. Вихідні дані

В даному розділі проводимо дослідження САР температури в пропарювальному котлі (контур 1 на ФСА).

Об’єктом регулювання є пропарювальний котел. Вихідною величиною даного об’єкту регулювання є температура в пропарювальному котлі, вхідною - переміщення регулюючого органу на трубопроводі пари, а збурюючою – витрата технологічної тріски.

Максимальна стрибкоподібна зміна регулюючої дії Y_макс=20 % переміщення РО.

Функція передачі каналом збурення ,

_{Вихідними даними для побудови моделі ОР каналом регулюючої дії є експериментальна крива розгону по температурі в пропарювальному котлі, отримана стрибкоподібною зміною переміщення РО на 8%.}

Вихідні дані занесені в таблицю 5.1.

Таблиця 5.1.

t, c	Т, °С
0	160.00
15	160.21
40	162.28
65	165.19
90	167.59
115	169.06
140	169.75
162	170.08
180	170.20
200	170.23

Якість регулювання в замкнутій САР характеризують такими показниками перехідного процесу:

• Максимальна динамічна похибка регулювання У_дин - це максимальне відхилення регульованої величини в перехідному режимі від її заданого значення. Ця похибка дорівнює першій амплітуді коливань регульованої величини у перехідному процесі (У_дин =А₁).

• Час регулювання τ_р - це час, протягом якого, починаючи з моменту дії збурення на САР, регульована величина досягає нового рівноважного значення з деякою заздалегідь встановленою точністю ± Δ і надалі не виходить за межі цієї зони. Час регулювання характеризує швидкодію САР.

• Перерегулювання регульованої величини φ - це виражене у відсотках відношення другої А₂ і першої А₁ амплітуд, спрямованих в протилежні сторони:

• Коефіцієнт заникання ψ:

• Час першого узгодження перехідного процесу t_пс - час, після закінчення якого керована величина перший раз досягає свого сталого значення (також характеризує швидкість протікання процесу в початковий період);

• Допустимий час досягнення першого максимуму - t_mах.

Вимоги до якості процесу регулювання:

1. Допустиме максимальне динамічне відхилення А₁=10 °С;

2.Допустима похибка регулювання  = ±1 °С;

3.Допустимий час регулювання t_p=280 с;

4. Ступінь коливальності m=0.24;

5. Друга інтегральна оцінка перехідного процесу за збуренням - min.

5.2. Побудова математичної моделі ор

Щоб розрахувати систему автоматичного регулювання даного контуру визначаємо математичну модель об'єкту. Математичну модель об'єкта регулювання для розрахунків оптимальних параметрів настройки регулятора знаходимо у вигляді функції передачі.

Побудуємо математичну модель за наявністю експериментальної знятої на об'єкті кривої розгону, яка відображає зміну температури в пропарювальному котлі від зміни положення регулюючого органа подачі пари на 8 %.

Щоб розрахувати систему автоматичного регулювання даного контуру визначаємо математичну модель об'єкту. Експериментальна крива розгону об'єкту регулювання температури в пропарювальному котлі представлена на рис.5.1.

Програма в середовищі Matlab для побудови експериментальної кривої розгону

clear,clc;

t=[0 15 40 65 90 115 140 162 180 200];

T=[160 160.21 162.28 165.19 167.59 169.06 169.75 170.08 170.20 170.23];

plot(t,T); grid; xlabel('t,с'); ylabel('T,^oC ');

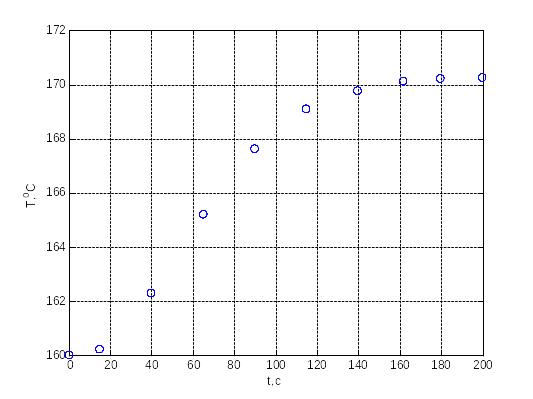
Рис.5.1. Експериментальна крива розгону, яка відображає зміну температури в пропарювальному котлі від зміни положення регулюючого органа на 8 %

Для зручності розрахунків експериментальну криву розгону об’єкта регулювання нормуємо діленням її значень на максимальну зміну вихідної величини .

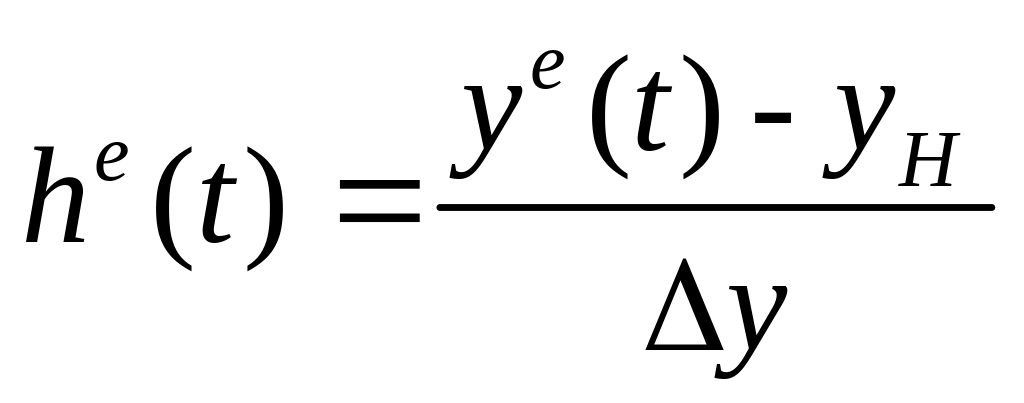
де значення вихідної величини після завершення перехідного процесу;

- початкове (номінальне) значення регульованої величини.

Програма в середовищі Matlab для побудови нормованої експериментальної кривої розгону

clear,clc;

t=[0 15 40 65 90 115 140 162 180 200];

T=[160 160.21 162.28 165.19 167.59 169.06 169.75 170.08 170.20 170.23];

Tzavd=160;

Tmax=max(T);

delT=Tmax-Tzavd;

Tout=(T-Tzavd)/delT;

figure(2),plot(t,Tout);xlabel('t,c');title('normovana kryva rozgonu ');grid;

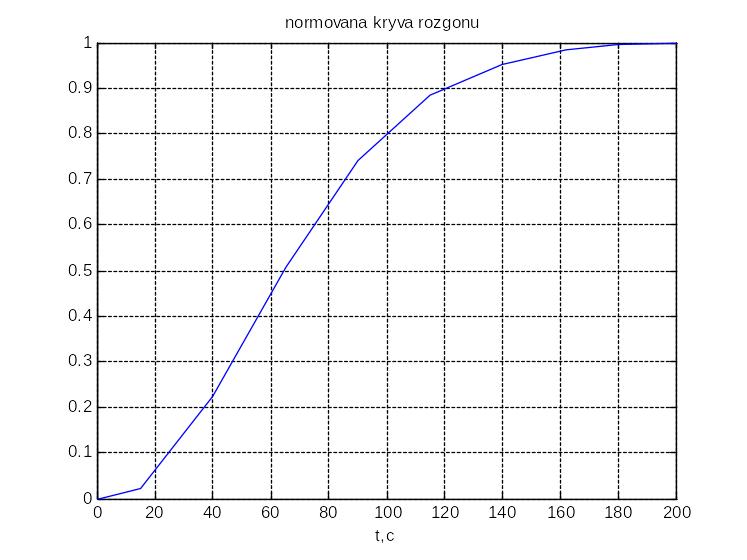
Рис.5.2. Нормована експериментальна крива розгону ОР

Відзначимо, що розмірний коефіцієнт передачі об’єкта регулювання з експериментальної кривої розгону визначається за формулою.

,

,

де значення стрибкоподібної зміни вхідної величини, яка викликала зміну вихідної величини.

Виходячи з характеру експериментальної кривої вибираємо передбачувану структуру моделі об’єкта і відповідну до неї функцію передачі в загальному вигляді послідовного з’єднання трьох аперіодичних ланок:

де Т₁, Т₂, Т₃ – сталі часу;

k – коефіцієнт передачі.