Дифференциал функции в точке
Определение:
Дифференциалом функции
в точке х0 называется главная
линейная часть приращения этой функции,
зависящая линейно от приращения
.
Дифференциал
функции равен
.
Дифференциал функции отличается от
приращения функции на бесконечно малую
более высокого порядка по сравнению с
величиной
,
поэтому это обстоятельство используют
для приближенных вычислений
откуда
.
Основные теоремы дифференциального исчисления
Теорема Ролля: Если функция
непрерывна на отрезке
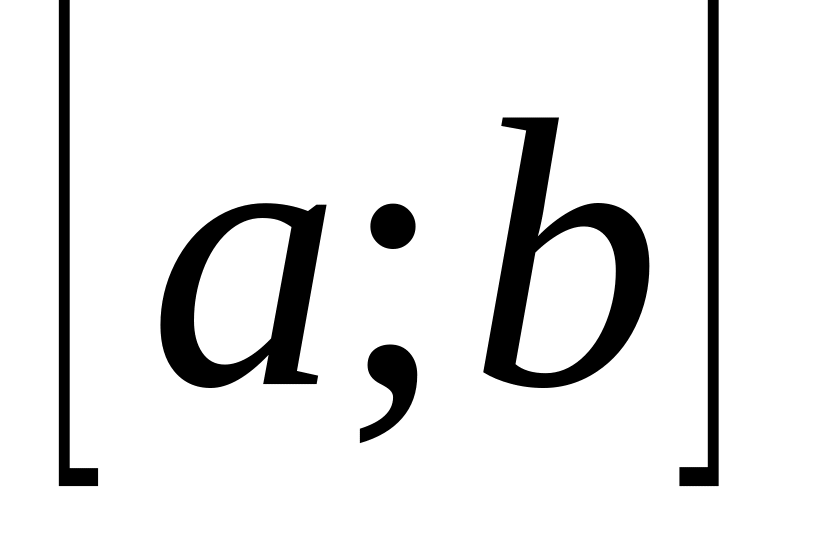,дифференцируема внутри этого отрезка,
имеет равные значения на концах отрезка, т. е.
,
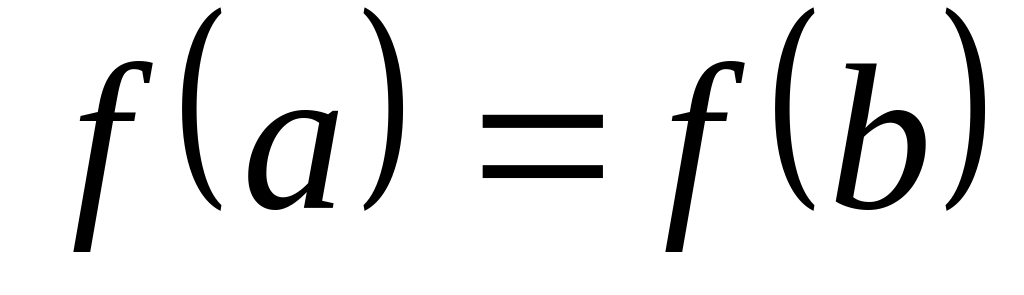то существует хотя бы одна точка x
= c (a < c
< b) такая, что
.
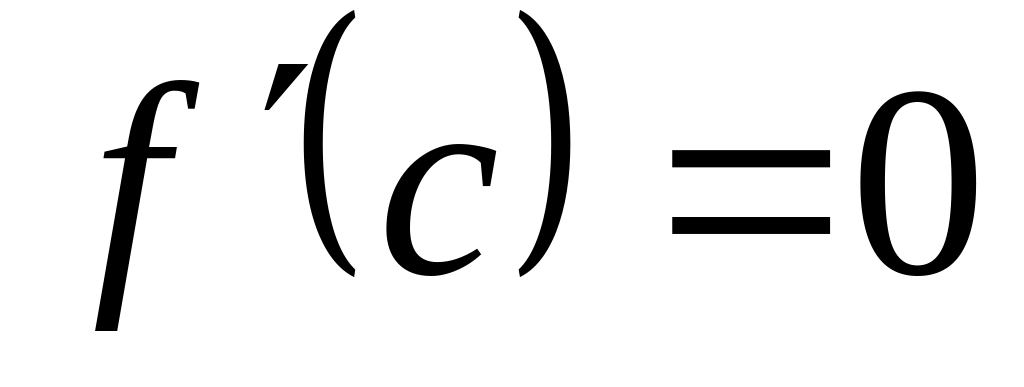Теорема Лагранжа: Если функция
непрерывна на отрезке ,
дифференцируема на (а, в), то существует хотя бы одна точка x = c (a < c < b), для которой выполняется равенство:
.
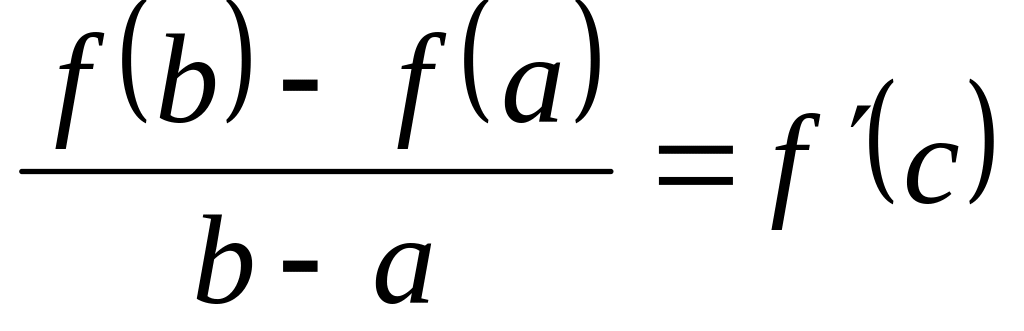Теорема
Коши: Если две функции
и
непрерывны на отрезке ,
дифференцируемы на (а, в), причем
,
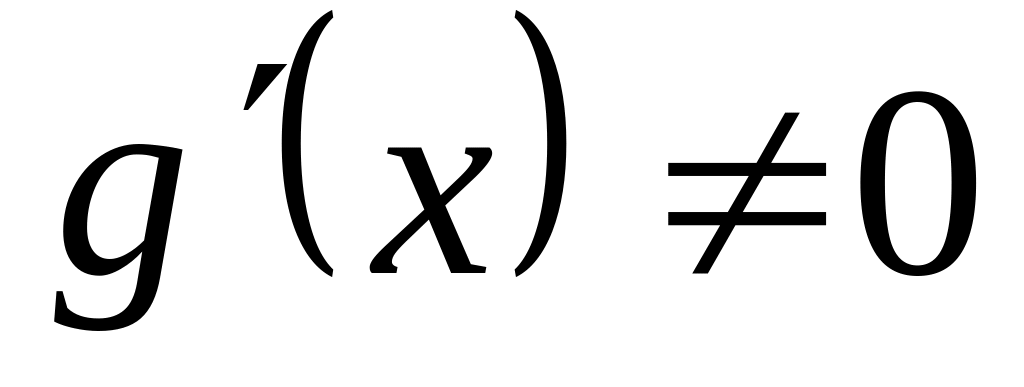то найдется такая точка x=c
(a<c<b),
для которой выполняется равенство
.
Если
и
или
и
,
то при вычислении предела отношения
этих функций будем получать неопределенности
вида
,
.
Для раскрытия этих неопределенностей
используют правило Лопиталя. Если
функции
и
удовлетворяют условиям теоремы Коши,
в окрестности точки
существует
,
то существует и предел
,
и эти пределы равны
=
.
Методы исследования функций и поведения их графиков.
Признаки возрастания функции (убывания функции)
• Если
дифференцируемая функция
возрастает (убывает) на некотором отрезке
,
то производная на этом отрезке
неотрицательна (неположительна), т. е.
.
• Если непрерывная функция дифференцируема и имеет положительную (отрицательную) производную на отрезке , то она возрастает (убывает) на этом отрезке.
Определение: Точки, в которых производная первого порядка обращается в нуль или терпит разрыв, называются критическими.
Теорема
(необходимый признак локального
экстремума): Если функция
имеет в точке
экстремум, то
либо
не существует.
Теорема
(первый достаточный признак локального
экстремума):
Пусть
является непрерывной на
,
причем
– критическая точка, функция является
дифференцируемой во всех точках
(кроме, может быть, самой
),
тогда: если
для всех
и
для всех
,
то в точке
функция
имеет максимум. Если
для всех
и
для всех
,
то в точке
функция имеет минимум.
Теорема
(второй достаточный признак экстремума):
Пусть функция
дважды дифференцируема и
– критическая точка, тогда если
,
то
– точка минимума; если
,
то
– точка максимума функции.
Теорема
(достаточное условие выпуклости графика
функции): Если во всех точках интервала
производная второго порядка функции
отрицательна (положительна), т. е.
(
),
то кривая выпукла вверх (вниз) на этом
интервале.
Теорема
(достаточный признак точки перегиба):
Если в точке
или
не существует и при переходе через эту
точку производная
меняет знак, то
является точкой перегиба.
Определение: Прямая называется асимптотой данной кривой , если расстояние от точки М кривой до прямой, при удалении точки М в бесконечность, стремится к нулю.
Если
,
то
– вертикальная асимптота.
Если
существуют пределы:
и
,
то прямая
– наклонная асимптота графика функции.
Если k = 0, y
= b – горизонтальная
асимптота.
Примерная схема исследования функций
Для исследования функции и построения графика надо:
Найти область определения функции.
Найти точки пересечения графика с осями координат, вертикальные асимптоты.
Исследовать функцию на четность, периодичность.
Исследовать на монотонность и найти экстремумы.
Найти интервалы выпуклости, точки перегиба.
Найти асимптоты графика.
Построить график функции.
Исследовать функцию
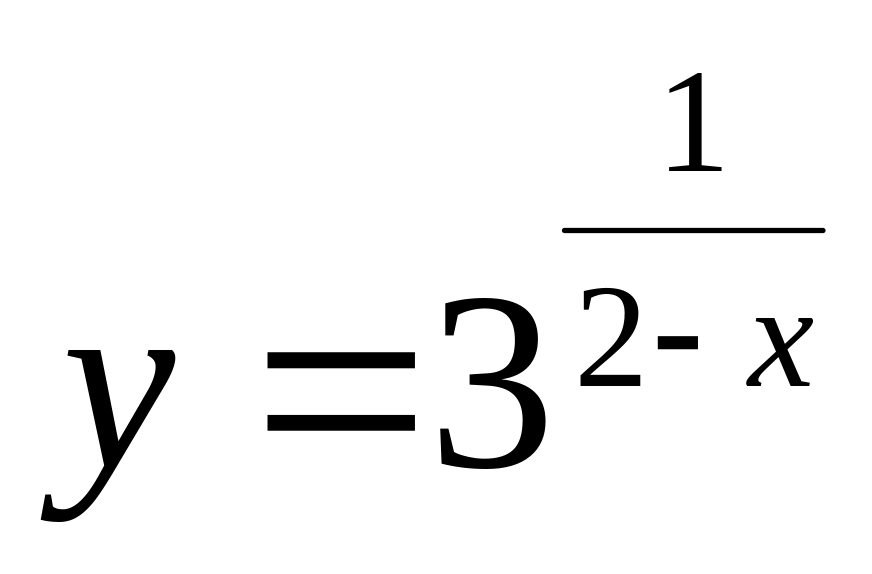и построить график.
Решение:
Областью определения функции является
множество всех действительных чисел,
кроме x = 2; прямая x
= 2 является вертикальной асимптотой
графика функции, так как
.
Функция принимает все положительные значения, кроме y = 1, так как
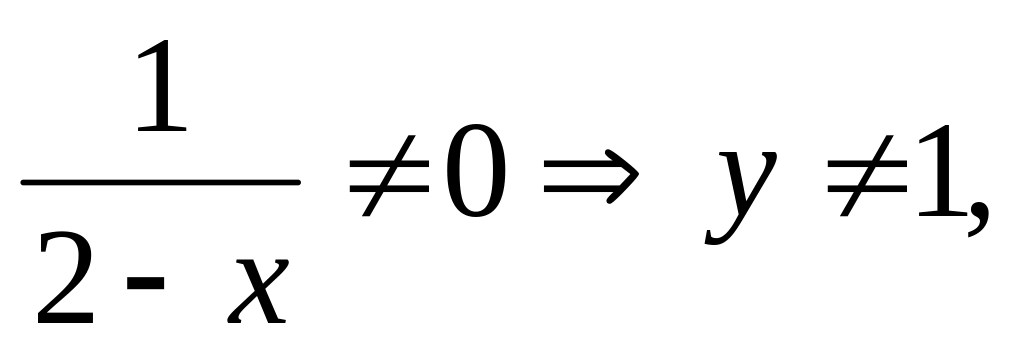при
.
;
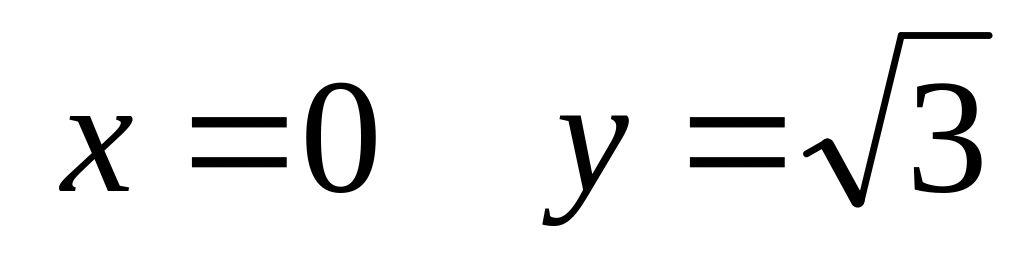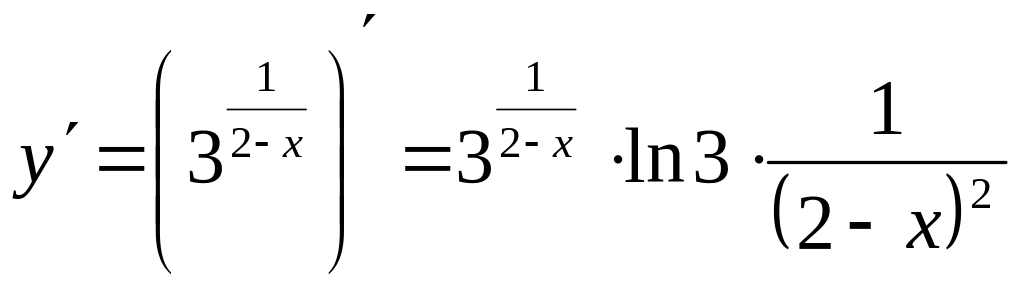но
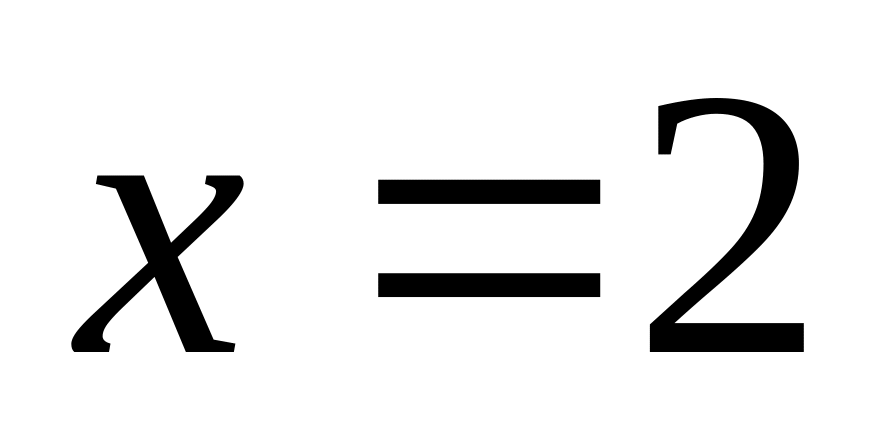– точка разрыва.
Х
3) Функция экстремумов не имеет и возрастает на каждом из промежутков.
4) Промежутки выпуклости функции:
;
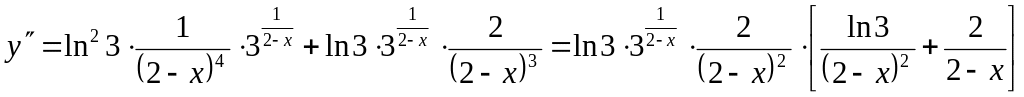при
и
– точка перегиба.
5)
Так как
,
то
– горизонтальная асимптота графика
функции,
– точка перегиба.
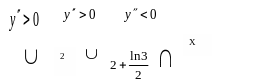
На основании проведенного исследования можно построить график.
Х