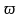8.3. Кездейсоқ әсер ету кезіндегі дәлдікті сараптау

Жалған жиілікті қолдану. 8.1 Суретте көрсетілген құрылымды сызба жүйе кірісіне белгілі корреляционды R_g (τ) функциясы бар тұрақты кездейсоқ үрдіс түрінде әсер ету арқылы қосылған жағдайда басқарудың динамикалық кателігінің орта квадратын e²_g (t) табу қажет. Берілген есепті шешу барысында жүйе кірісіндегі динамикалық түйін – беріліс функциясы бар W_d (p) = k_d инерционсыз.

Үздіксіз берілген әсер етушіден g (t) корреляционды функциясы және спектралды тығыздығы 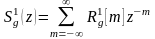бар тор тесікті g[n] = g(nT) функцияға өтеміз.

Бастапқыда алынған, яғни жүйенің алшақты түйісінің дискретті беріліс функциясын енгіземіз , Мұндағы дискретті беріліс функциясы 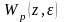формуламен сипатталады (8.1). Сонымен қатар тұйық жүйенің дискретті беріліс функциясын енгіземіз

, (8.13)

және қайта z – өзгертуден торлы функция қызметін атқарады. Түйін формуласын қолдану көмегімен белгілі уақыт моменті аралығында динамикалық қателік мәнін келесі түрде көрсетеміз

,

(8.14)

Басқа уақыт моменті үшін t санынан m бүтін санға қалып қойған дискретті кезең үшін сәйкес (8.14) түрде көрсетеміз

(8.15)

Теңдіктің оң және сол жақтарын көбейту (8.14) және (8.15), сонымен қатар n дискретті уақыт бойынша (қателіктің корреляциялық функциясы үшін) орталауды туындату арқылы аламыз

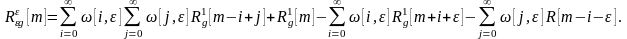
(8.16)

Орны өзгертілген торлы функцияның спектралды тығыздығын e_g [n, έ] корреляциялық функцияның екі жақты қайта z- өзгеруі ретінде анықтаймыз (8.16)

(8.17)

(8.16) және (8.17) мәндерін қою арқылы корреляциялық функция аргументтері үшін жаңа ауыспалыларды енгіземіз, яғни соммалау тәртібін өзгертеміз

(8.18) формуласынан z- қайта өзгеру қасиеттеріне сәйкес, аламыз

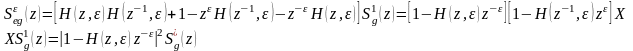
немесе псевдожиіліктің көрсеткішіне z = (1+ j λ T / 2) / (1– j λ T/ 2) ауысу көмегімен

Уақыттың дискретті моментінде t = (n + έ) T қарастырылатын динамикалық қателіктің орта квадраты келесі түрде құралады

(8.20)

έ барлық мүмкін мәндері бойынша (8.20) формуласын интегралдау үздіксіз уақыттағы орталандыру кезіндегі қателіктің орта квадратын береді

(8.21)

έ еркін түрде алынған мәні кезінде (8.20) формула бойынша аналитикалық интегралдауды орындау мүмкін емес болса, онда тек үш мәнмен ғана: έ = 0, έ = 1/ 2 және έ = 1 – 0 шектелуге болады. Себебі λ < 2 / Т

έ көрсетілген барлық мәндері үшін спектралды тығыздық псевдожиілік квадратының бөлшекті-рационалды функциясына сәйкес келумен қатар интегралдауға беріледі. Яғни, мәнін бағалау үшін (8.21) формуласының орнына Симпсон бойынша жуық интегралдау формуласын қолданамыз

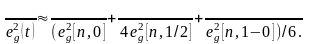(8.22)

(8.19) – (8.22) формулаларын ауыспалы функция кезінде жуық есептеу үшін қолдануға болады. Ол үшін импульстті элементті (8.1 Сур.қараңыз) шартты түрде үздіксіз динамикалық түйін шығысынан кірісіне ауыстыру керек, ал жиілікті беріліс функциясынан 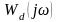импульстті фильтрдің жиілікті беріліс функциясына өту қажет. Мұндай эквивалентті импульстті фильтрдің дискретті беріліс функциясы келесі түрге ие бола алады

Берілген мәнді (8.13) формуласына беріліс коэффициентінің орнына қою қажет.

(8.19) – (8.21) формулалары дискреттілік кезеңінің «тұрақты емес» қателігін зерттеу үшін пайдалы. Егер жүйе кірісінде тұрақты кездейсоқ үрдіс түрінде белгілі спектралды тығыздығы бар үдемелі ықпал берілсе, онда басқарудың орын ауыстырған қателігінің спектралды тығыздығы келесі формула бойынша анықталады

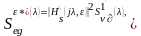(8.23)

Мұндағы жиілікті беріліс функциясы (8.4) бойынша дискретті беріліс функциясына сәйкес келеді, ал формулада спектралды тығыздық z = (1+ j λ T / 2) / (1- j λ T / 2) мәнінің алмастырушысы ретінде берілген

Мұндағы АЦП кірісіндегі әсер етушінің спектралды тығыздығы бар корреляциялық функциясы.

Қалыпты жиілікті қолдану. Басқару қателігінің орта квадратын спектралды әдіспен нақты сараптауды қарастыратын болсақ, динамикалық түйіннің 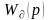беріліс функциясы кезінде дұрыс шешім болып табылады. Жиілік спектрлерін λ псевдожиілік кезінде емес, керісінше ω жиілік функциясы кезінде қолданамыз.

Қателіктің динамикалық негізін зерттеуден бастайтын болсақ 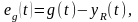мұндағы әсер етушіге жүйе реакциясы. үздіксіз функциялардың Фурье сипаттамасы болсын (шартты түрде оларды жоққа шығармаймыз). Онда үздіксіз динамикалық түйін мен импульс элементі тағайындалғаннан кейін сигналы Фурье сипаттамасының түріне сәйкес келетіні ықтимал [33, 111].

(8.24)

Мұндағы – уақыт бойынша кванттау жиілігі.

8.1 Сурете көрсетілген жүйенің құрылымды сызбасына сәйкес, келесі қатынастар орынды

(8.25)

(8.26)

Мұндағы

(8.27)

(8.25) формуласын ескере отырып, (8.24) формуласын (8.26)-ға ауыстыру және j ω мәнін 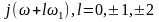аргументіне алмастыру келесі жүйелікті алуға мүмкіндік береді

(8.28)

(8.28) теңдігінің оң және сол жақтарын мәніне көбейту және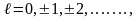 ,болған жағдайда оң және сол жақтың соммаларын табу арқылы қайта құрудан алатынымыз

(8.29)

Мұндағы

(8.30)

Егер (8.28) формуласында l=0 десек, (8.29) (8.30) (8.27) теңдіктерін ескере отырып, алатынымыз

(8.30)

(8.31) формуласынан және (8.25) тұйықталу теңдігінен пайда болатыны

(8.32)

(8.30) ескере отырып (8.32) теңдігі бойынша Фурье сипаттамасынан спектралды тығыздыққа ауысу көмегімен үздіксіз стационарлы кездейсоқ үрдіс ретінде басқарудың динамикалық қателігінің спектралды тығыздық мәнін анықтаймыз

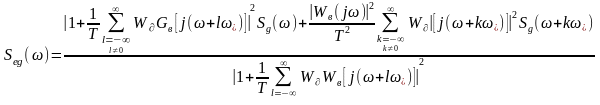(8.33)

Динамикалық қателіктің орта квадраты

(8.34)

(8.33) ескере отырып (8.34) сандық интегралдау кезінде спектр еніне баланысты жоғарғы шекті соңғы деп есептеуге және (8.33) теңдіктегі бірнеше мүшелерді соммалаумен ғана шектелуге болады. Қателіктің спектралды тығыздығы үшін (8.33) теңдігінен спектралды тығыздығы бар стационарлы кездейсоқ үрдістің ықпалынан (8.1Суретін қараңыз) келесі формуланы алуға болады

(8.35)

Қателікті сараптау мысалы.

болған жағдайда басқарудың динамикалық қателігінің орта квадратын анықтаймыз.

Жүйе кірісінде үздіксіз түйін инерционсыз болғандықтан, қателіктің орта квадратын қарастырылған екі әдіспен табу арқылы нәтижелерін салыстыруға болады. (8.13), (8.19) және (8.20) формулалары арқылы анықтайтынымыз

(8.22) формуласы береді. Уақыттың үздіксіз функциясы ретінде қателіктің орта квадратының нақты мәнін (8.27) (8.33) (8.34) формулалар негізінде есептейміз. Ол 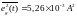мәнін құрайды. Осылайша, екі әдіс көмегімен жуық нәтижелерге қол жеткізуге болады.

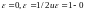кезде мәндері елеулі түрде өзгешеленеді және сәйкес түрде 1:0,31:4,0 қатынасында болады. Сондықтан қарастырылған мысал бойынша, әсіресе жүйенің үздіксіз бөлігінің кіші инерциялығы кезінде басқарудың дәлдігін , тіптен 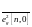шамалары бойынша бағалау бұрыс болып шығуы ықтимал.

8.4. ҮЗДІКСІЗ ПРОТОТИП БОЙЫНША ЖҮЙЕНІҢ САНДЫҚ БӨЛІГІН СИНТЕЗДЕУ

Үздіксіз басқару қондырғысын сандықпен алмастырумен байланысты, басқару қателіктерінің туындау заңдылықтары. Аналогты-сандық жүйенің сандық бөлігін синтездеу кезінде, 8.1 п. көрсетілгендей, идеал үздіксіз жүйе бойынша қарастырған жөн, динамикалық қасиеттерді оптимизациялау әдістері жақсы өңделген және қарапайым. Бұл жағдайда келесі мәселе туындайды.

Wд(р)

W_нуу(р)

W_н(р)

g(t) y(t)

а )

W_э(p)

ЦУУ

б

Wд(р)

⟟

D(Z)

⟘

W_н(р)

)

g (t) y(t)

T T

Синтездеу жүйесі бойынша үздіксіз прототиптің құрылымды сызбасы:

а – бастапқы вариант, б – аналогты-сандық вариант.

(8.4, а Суреті) беріліс функциялары бар дәйекті түрде қосылған үш түйінді туындататын контурлары бар үздіксіз жүйе берілген. Синтезделетін аналогты-сандық жүйедегі беріліс функциялары бар үздіксіз түйіндер сақталатыны белгілі, ал беріліс функциялары бар үздіксіз басқару қондырғысының орнына АЦП, ЦАП және беріліс функциясы бар экстраполятор (8.4, б) көмегімен жүйенің үздіксіз бөлігімен байланысқан, D (z) дискретті беріліс функциясы бар сандық басқару қондырғысы (СБҚ) қолданылады. Осы сандық элементтер мінездемелерін аналогты-сандық жүйе және үздіксіз жүйе-прототиптің динамикалық қасиеттері сәйкес келетіндей таңдау қажет. Үздіксіз динамикалық фильтрдің дискретті аппроксимациясы деп аталатын бұл мәселені нақтылау үшін үздіксіз және сандық басқару қондырғыларының түбегейлі ерекшеліктерін анықтау қажет. Яғни ерекшеліктер бастапқы жуықтау кезінде жеке түрде қарастырылатын уақыт және деңгей бойынша кванттау әсерімен байланысты екені белгілі.

Деңгей бойынша кванттау көмегімен қателіктерді анықтау 6.1, 7.2 және 8.2 бөлімінде сарапталған. Олар σ_А және σ_Ц мәндері төмендеген сайын азаяды. Деңгей бойынша кванттау көмегімен қателіктердің туындау заңдылықтарын импульстті элемент арқылы өтетін сигнал спектріндегі өзгерістерді қарастыру кезінде сараптау ыңғайлы. ырғақты жиілікке тең кезеңмен қатар импульстті элемент шығысындағы сигнал спектрі периодты болып табылады және бастапқы үздіксіз сигнал спектрімен график арқылы бейнеленетін қатынас (8.5 Сурет) арқылы байланысқан.

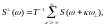
Осы графиктерге сәйкес және Котельников теоремасы бойынша уақытша кванттау кезінде ақпараттың жоғалуы теория түрінде сигнал спектрінің ені бойынша жиілікпен шектелсе ғана мүмкін емес.

(8.36)

спектрінің орталық парциалды аумағы (8.5, а Сурет) кезінде көлемі бойынша шығыс спектрімен толық сәйкес келеді, сонымен қатар берілген аумақтағы фазалық қатынастар өзгеріссіз қала береді. Сондықтан шығыстағы үздіксіз сигнал теория түрінде, яғни дискретті сигналды 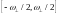жиілік интервалындағы бірқалыпты нығайтуды қамтамасыз ететін төменгі жиіліктегі идеал фильтр арқылы өткізу жолымен ғана қалпына келтіруге болады. Сонымен қатар фаза бойынша орын ауыстырусыз орындалады (сипатталған фильтр бойынша АЧХ 8.5, а Суретінде штрихтік сызықпен бейнеленген). Бірақ тәріздес фильтр физикалық тұрғыдан іске аспайды, себебі оның импульсттік сипаттамасы t < 0 болған жағдайда нөлге тең емес. Іс жүзінде төменгі жиіліктегі реалды фильтр кіші жиіліктегі аумақта бірқалыпты АЧХ және нөлдік ФЧХ-ға ие бола алса, онда (8.36) теңсіздікті орындау кезінде ғана үздіксіз сигнал қатесіз қалпына келе алады. Егер (8.36) қатынасы орындалмаса, онда сигнал уақыты бойынша квантталған спектрдің әр түрлі аумақтарының өзара беріліс функциясы орындалады (8.5, б Сурет). Нәтижесінде іріктемелер бойынша үздіксіз сигналды қалпына келтіру мүмкіндігі жойылады, яғни дискретті басқару қателігінің ұлғаюына әкеп соғады.

а)S(w+w₂) S(w) S¹(W)T S(w-w₁) а)/ W₃(jw)/T^-1

АЧХ 1

. 0

-w₁ -w_ГР 0 w_ГР w₁ W 0,5П П 1,5П wT

б ) S¹(W)T б)

- П

2

-П

- 3П 0,5П П 1,5П wT

- w₁ -w_ГР 0 w_ГР w₁ W 2

arg W₃(jw)

Сур. 8.5. Уақытша кваттаудан өткен спектр дабылы, а-теңсіздік (8.36) орындалуда, б-теңсіздік (8.36) орындалмауда

Сур. 8.6 Экстраполяторлардың жиелік сипаттамалары: а-АЧХ, б-ФЧХ;

-----нөлдік экстраполятор реті; — бірлік экстраполятор реті; —• —• —

мінсіз экстраполятор реті

Ақпаратты тасымалдауға қабілетті кез-келген сигналдың спектрі теория жүзінде ені бойынша шектеле алмайды, ал тәжірибе жүзінде әрқашан жиілікте белгілеуге болады. Сонымен бірге сигнал қуаттылығының негізгі, алдын ала берілген бөлігіне тураланған шектеу бойынша жиілік интервалы айқындалады. Кері байланыс принципіне сәйкес, жүйе шығысында байқалған нақты және қажет мәндердің арасында туындаған айырмашылыққа басқару арқылы тиісті шаралар қолданады да, ақырында сол айырымды азайтады не болдырмайды. Бұл үрдіс лезде өтпейді, әйтсе де ол жүйенің қосылған барлық элементтерінің инерциясына сәйкес дер кезінде өрістейді. Іс жүзінде уақыт мерзімі ішінде қателікті жою үрдісі туралы толық ақпараттан гөрі, сол үрдістің тек соңғы нәтижесі маңызды болады. Осы ахуалға жүйе статикасының сараптамасы жатады, яғни жүйе қателігінің тағайындалған мәнін бағалау, не болмаса басқарылмалы айнымалылардың нақты және қажет мәндері арасындағы айырмашылық.

Сыңар контуры бар құрылымдық сызбамен сипатталған басқару нысанына басқарылмалы айнымалының қажет мәнінен ауытқуына әкелетін әсер сигналы әрекет етеді. Қорытқы қателік – жүйенің қоздыратын әсеріне жауабы.

Берілетін сигналдың өзгерісі болады, бірақ инерция салдарынан жүйе берілетін әсердің жаңа мәніне дереу ие бола алмайды. Еркін қозғалыс элементтерінің кему нормасы жүйенің сәйкес полюстерінің нақты бөліктеріне тәуелді, ал кіріс сигналының түрімен амплитудасына тәуелсіз болады деп түсіну қажет. Әйтсе де өтпелі сипаттама еркін қозғалыс элементтерін реттеу көрнектілігін қамтамасыз етеді.

U_з(t)

0 2 3 4 5 6 9 10 11 12 tT^-1

Сандық сараптама бойынша туындысы бар функцияны инерполяциялық полиноммен алмастыруға болатыны айқын. Сондықтан идеал қондырғыны қолданған жағдайда да, ЦУУ қолдану көмегімен басқарудың үздіксіз заңы дәлдікпен іске аспайды.

Сандық бөліктің дискретті беріліс функциясын анықтау. ЦУУ қызметінің алгоритмі ЦУУ динамикалық қасиеттерінің жақындығын және оның идеал үздіксіз прототипін қамтамасыз етуі қажет деген жоғарыда жасалған қорытынды нақты болып табылдмайды, себебі белгіленген жақындықты р түрлі түсінуге болады және әрқашан белгілі бір шамада бір жақты болып табылады. Бірнеше вариантын қарастырайық.

АЦП ЦУУ кірісіне және беріліс функциясы бар ЦУУ үздіксіз прототип кірісіне, екеуіне бірдей синусоидальді сигнал берілсін. Сонымен қатар үздіксіз сызықты қондырғының шығысында амплитудасы мен фазасы өзгеше синусоидальді сигнал орнатылсын. ЦУУ экстраполятор шығысында 8.7 Суретінде біртұтас сызықпен көрсетілген, сатылы сигнал болсын. Дискретті момент уақыты t=nT бойынша шығыс сигналдарының мәндері сәйкес келсе, онда сандық және үздіксіз қондырғылар қасиеттері жақын деп есептеуге болады. Онда дискретті беріліс функциясын 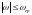жиіліктің жұмыс диапазонында келесі шарт орындалатындай таңдау қажет.

. (8.37)

Бұл жағдайда экстраполятор идеалсыздығы ескерілмейді.

Егер басты талап ретінде үздіксіз басқару қондырғысының шығыс сигналы мен экстраполятор шығыс сигналының негізгі гармоникасының (8.7 Сурет, штрихті сызық) сәйкестігін қойса, онда (8.37) шартының орнына келесі шартты қою қажет

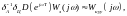
Яғни экстраполятор жағдайында нөлдік ретті береді

. (8.38)

ЦУУ және жүйенің үздіксіз бөлігін бүтін түрде қарастыру арқылы шығыс сигналының t=nT уақыт моменттерінде y (t) аналогты-сандық жүйемен оның үздіксіз прототипінің сәйкестігін талап етсе, онда D (z) мәнін таңдау мақсатында келесі қатынасты қорытындылаған жөн

(8.39)

Мұндағы үздіксіз бөліктің дискретті беріліс функциясы келесі түрге ие болады

.

(8.37)- (8.39) қатынастарынан кез–келген жағдайда ЦУУ дискретті беріліс функциясы белгіленген қатынастың оң жағы болып табылатын (кешенді аргументтің рационалды функциясы ) кешенді аргументтің рационалды функциясының аппроксимациясына аударылатыны байқалады. Әрі қарай дәлдік үшін қатынас негізі ретінде (8.37) қатынасын қабылдаймыз, дегенмен ол қарастырылып отырған мәселенің жалпы сипаттамасына әсерін тигізбейді.

(5.61) формуласымен анықталатын псевдожиілікті қолдану көмегімен ЦУУ жиілікті беріліс функциясын анықтаймыз

(5.61) формуласына сәйкес қалыпты жиілік псевдожиілікпен келесі қатынаста байланысты

немесе

(8.40)

мұндағы 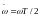және – салыстырмалы жиілік және псевдожиілік.

Арктангенсті деңгейлі қатарға жіктеу арқылы (8.40) формуласынан алатынымыз

(8.41)

(8.41) шексіз қатарда бірінші l мүшелерімен шектелу және ЦУУ жиілікті беріліс функциясы үшін (8.37) критерийін қолдану көмегімен келесі формулаға ие боламыз

(8.42)

Ізделіп отырған ЦУУ дискретті беріліс функциясы мына түрде сипатталады

(8.43)

Ал ықылас жиілікті беріліс функциясын іске асырудағы қателік – формула бойынша:

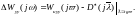(8.44)

Қарапайым жағдайда l = 1 болған кезде (8.43) және (8.42) формулаларынан алатынымыз:

(8.45)

(8.46)

Салыстырмалы төмен жиіліктегі λ ≈ ω болған кезде қалаулы ЦУУ жиілік сипаттамаларын іске асыру дәлдігін (8.45) формуласы қамтамасыз ете алатыны (8.46) формуласынан айқын. Бірақ өзінің қарапайымдылығы бойынша жиі қолданылады. Осы формуланы қолдану кезінде псевдожиілік функциясында құралған ЦУУ логарифмдік жиілік сипаттамалары оның ω жиілік функциясында құралған үздіксіз прототипінің логарифмдік жиілік сипаттамаларымен көлемі бойынша сәйкес келетіні өте маңызды.

Үздіксіз модель түйіндерін сандық интегралдау әдістерінің бірін іске асыратын, дискретті интегралданатын түйінмен алмастыруға болады, мысалға трапеция әдісіне сәйкес x (t) интеграл функциясы келесі формуламен есептелінеді

.

Үздіксіз интеграторларды трапеция формуласымен қызмет ететін дискреттімен алмастыру көмегімен 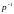бірлік интеграторлардың беріліс функцияларының орнына 0,5T(z+1)/(z-1) дискретті беріліс функциялары қойылады. Яғни (8.45) формуласында сипатталатын өзгеріс орындалады. Осылайша, (8.45) формуласымен анықталатын ЦУУ дискретті беріліс функцияларын, яғни ЦУУ үздіксіз прототипінің беріліс функциясын трапеция формуласы бойынша дискретті интегралдаудың орнына алмастыру нәтижесі деп қабылдауға болады.

Егер l > 1 болған жағдайда (8.43) формуласын қолданатын болсақ, ЦУУ қалаулы қасиеттерін іске асыру дәлдігі жоғарлайды. Мысалға, l = 2 болса, ол үздіксіз интегралдау операторларын дискретті интегралдау операторларымен «3/8» Симпсон әдісі бойынша алмастырудың нәтижесі деп қарастыруға болатын D (z) функциясын береді.

Екінші жағынан, кез–келген сандық интегралдау әдісі үздіксіз интегралдау операторларын дискретизациялау кезінде қолданысқа ұшырайды. Осы кезде ЦУУ дискретті беріліс функциясының көрінісі (8.43) формуласының айқын көрсеткіші болып табылады. Аттас көрсеткіштер арасында «1/3» Симпсон және Уэддль әдісі бойынша алынатын мәндер келесі түрде айқындалады:

(8.47)

(8.46)

(8.43), (8.47) және (8.48) формуласында сипатталатын D (z) функциясын анықтау әдістері p кеңістігінде бірлік радиусы z бойынша осьтік нүктелерді айқындауды қамтамасыз ететіндігімен ерекшелінеді.

[29, 33, 60, 89] үздіксіз прототипі бойынша сандық қондырғыларды синтездеу әдістерінің сан түрі бар, соның ішінде көбісі аналогты-сандық жүйенің ЦУУ дискретті беріліс функциясын анықтау үшін қолданылады.

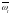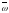Қалаулы жиілік сипаттамаларын іске асыру қателігін бағалау. ЦУУ беріліс функциясының жиілік қателігі үшін (8.44) формуласын зерттейміз. Ол үшін жиілік шкаласының сызықты емес деформациясының туындысы, сонымен қатар және салыстырмалы жиіліктерді енгізу көмегімен келесі қатынасты өрнектейміз

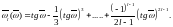(8.49)

Онда (8.44) көрінісін өзге түрде жаза аламыз

(8.50)

l = 1 болған жағдайда (8.49) формуласы теңдігін береді.

(8.50) формуласы (8.47) және (8.48), сонымен қатар «1/3» Симпсон және Уэддль әдістеріне негізделген қатынастар сипатталатын синтездеу әдістерін айқындайды. Ол үшін орнына келесі функцияны қолдану абзал:

(8.51)

(8.52)

және 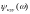– ЦУУ бойынша АЧХ және ФЧХ үздіксіз прототипі, яғни.

(8.50) формуласын ескере отырып, ЦУУ қалаулы жиілік беріліс функциясын іске асырудағы амплитудалық және фазалық қателігін ω_гр шектеулі жиілік мәндерімен сипаттаймыз:

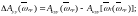(8.53)

(8.54)

(8.43), (8.47) және (8.48) формулаларын қолдану кезінде және 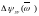функциялары – кезінде бір қалыпты үдеушілер. Сондықтан 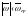жиілігіндегі ЦУУ жиілік сипаттамаларын іске асыру дәлдігі кезіндегіге қарағанда жоғарырақ. Бұл жағдай үшін және теңсіздіктер түрінде берілген максималды амплитудалы және фазалық қателіктер кезінде теңсіздіктің орындалуын бақылай алады:

функциясын нүктесінде дифференциалданатын деп есептей отырып, (8.53) формуласын осы функцияның туындысын аргумент арқылы сипаттау көмегімен белгілейміз:

(8.56)

функциясын енгіземіз немесе (8.49) формуласын ескере отырып,

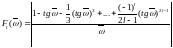
Онда (8.55) және (8.56) көріністерінен алатынымыз

Бұл жағдай функциясы үшін талап қояды

(8.58)

функциясының мәндері

	F1( )	F2( )	F3( )	F4( )	F5( )
0,05	8,34*10-4	1,25*10-6	2,23*1011	1,31*10-11	8,70*10-12
0,10	3,35*10-3	2,02*10-5	1,45*10-7	1,12*10-9	2,52*10-11
0,15	7,59*10-3	1,03*10-4	1,69*10-6	2,99*10-8	5,59*10-10
0,20	0,0135	3,32*10-4	9,74*10-6	3,11*10-6	1,05*10-7
0,25	0,0214	8,30*10-4	3,85*10-5	1,95*10-6	1,04*10-7
0,30	0,0311	1,77*10-3	1,20*10-4	8,91*10-6	6,96*10-7
0,40	0,0570	6,00*10-3	7,58*10-4	1,05*10-4	1,52*10-5
0,50	0,0926	0,0161	3,37*10-3	7,75*10-4	1,88*10-4
0,60	0,140	0,0377	0,0123	4,41*10-3	1,67*10-3
0,70	0,203	0,0813	0,0398	0,0215	0,0123
0,80	0,287	0,168	0,122	0,0975	0,0831
0,90	0,400	0,341	0,365	0,436	0,554
1,00	0,557	0,702	1,13	2,04	3,95
1,10	0,786	1,51	3,81	10,9	33,2

Сәйкес талапты (8.55) шарттарын ескере отырып (8.54) берілген фазалық қателіктер мәнінен алуға болады. Яғни оларды (8.58) шартымен біріктіру көмегімен, нәтижесінде:

(8.59)

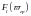
(8.59) қатынасы «1/3» Симпсон және Уэддль әдістерін қолдану кезінде де өз күшін сақтайды, яғни егер (8.51) (8.52) формулаларын ескере, сол жақ бөлігін немесе -ке алмастырса.

түрлі мәндері кезінде және функцияларының мәндері 8.1 Кестеде берілген.

8.1 Кестеде берілген көрсеткіштердің сараптамасы D (z) функциясын анықтаудың түрлі әдістерін қамтамасыз ететін ЦУУ жиілік сипаттамасының іске асыру дәлдігін салыстыруға мүмкіндік береді. немесе 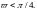кезінде (8.41) формуласы бойынша қатарларға жіктейміз. Мысалға, жиілігі үшін қарапайым әдіс (l = 1) өлшемімен сипатталады. Дәл сондай өлшем 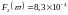l = 2 болған жағдайда жиілігінде жеткізіледі, яғни бес есе үлкен.

8.1 Кестесі

функциясы

Fc( )	Fy( )
5,56*10-7	1,11*10-9
8,33*10-6	7,72*10-8
4,55*10-5	8,96*10-7
1,45*10-4	5,16*10-6
3,58*10-4	2,03*10-5
7,52*10-4	6,33*10-5
2,46*10-3	3,96*10-4
6,25*10-3	1,76*10-3
0,0137	6,47*10-3
0,0269	0,0215
0,0490	0,0735
0,0845	0,330
0,139	2,69
0,219	0,74

Бірақ, дискретті беріліс функциясының тәртібі l = 1 болған жағдайға қарағанда үш есе жоғары. l = 2 болған кездегі есептеуіштің өнімділігі l = 1 болған жағдайға қарағанда 1,67 есе аз. 8.1 Кестесі бойынша басқа әдістерге сәйкес сандар келесі құрылымды құрайды: l = 3 болған кезде 1,60 есе; l = 4 болған кезде 1,43 есе; l = 5 болған кезде 1,22 есе; «1/3» Симпсон әдісі кезінде – 3 есе; Уэддль әдісі бойынша – 2,25 есе. Қарастырылған мысалдан талап етіліп отырған дискретті аппроксимация дәлдігі жоғары екені байқалады, есептеу шығындарын үнемдеу мақсатында тиімді әдіс болып «1/3» Симпсон әдісі табылады.