Контрольна робота № 5 Тема: Подібні трикутники
Варіант 1
Частина 1
Завдання 1 – 8 мають по п’ять варіантів відповідей, з яких тільки ОДНА ПРАВИЛЬНА. Оберіть правильну, на вашу думку, відповідь.
1. Відомі сторони двох трикутників. Обрати такі сторони, щоб трикутники були подібні
А |
Б |
В |
Г |
Д |
20, 15, 36 30, 14, 56 |
36, 28, 20 45, 56, 40 |
35, 28, 21 5, 4, 3 |
25, 45, 14 5, 9, 7 |
15, 24, 45 5, 8, 12 |
2. Трикутник АВС подібний трикутнику КТР. АВ = 15, КТ = 20, периметр трикутника АВС дорівнює 48. Знайти периметр трикутника КТР.
А |
Б |
В |
Г |
Д |
60 |
64 |
68 |
56 |
54 |
3. Cторони трикутника відносяться як 5:7:9. Знайти сторони подібного йому трикутника, периметр якого дорівнює 84.
А |
Б |
В |
Г |
Д |
20, 15, 36 |
36, 28, 20 |
35, 28, 21 |
25, 45, 14 |
15, 24, 45 |
4. Точка перетину діагоналей трапеції поділяє одну з діагоналей на відрізки завдовжки 7 см і 11 см. Менша основа дорівнює 21 см. Знайти більшу основу
А |
Б |
В |
Г |
Д |
14 см |
26 см |
28 см |
33 см |
24 см |
5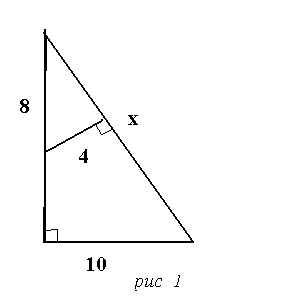
.
За рисунком 1 знайти х
А |
Б |
В |
Г |
Д |
16 |
15 |
20 |
30 |
24 |
6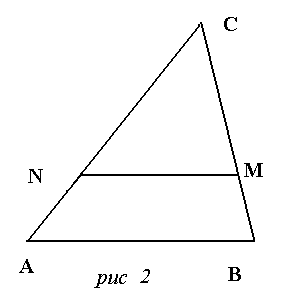
.
В трикутнику АВС (рис. 2) MN
// AB. CM = 15,
MN = 16,
CB = 18. Знайти АВ.
А |
Б |
В |
Г |
Д |
19,2 |
18,6 |
32 |
18,2 |
24 |
7. Хорди АВ і МК перетинаються в точці С. АС = 15, СВ = 6,
СМ = 3. Знайти СК.
А |
Б |
В |
Г |
Д |
32 |
10 |
40 |
50 |
30 |
8. На рисунку 3 зображений паралелограм АВСD. М – середина АВ, К – середина ВС. Знайти пару подібних трикутників.
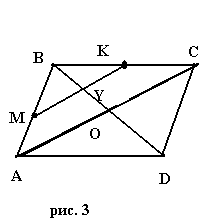
А |
Б |
В |
Г |
Д |
|
|
|
|
|
і
і
і
і
і
Частина 2
З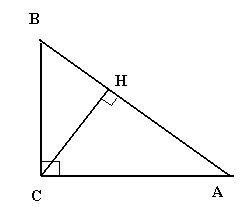
авдання
9 передбачає установлення відповідності
між заданими значеннями
(1 – 4) і відповідними
їм значеннями (А
– Д).
9. Дано прямокутний трикутник
АВС (
).
СН – висота. Поставити у відповідність
заданим відрізкам (1-4)
Значення невідомих відрізків А – D.
1 |
ВС = 3, СН = 2,4 , ВН = 1,8, АС = … |
|
А |
7,2 |
2 |
ВА = 10, ВС = 6 , СА = 8, НС = … |
|
Б |
4,4 |
3 |
СН = 9,6, АН = 12,8, НВ = … |
|
В |
4,8 |
4 |
АС = 20 ,АН = 16, СВ = 15, СН = … |
|
Г |
12 |
|
|
|
Д |
4 |
Частина 3
Завдання 10 -11 відкритої форми з короткою відповіддю.
Розв’яжіть завдання та запишіть відповіді.
10. Висоти паралелограма дорівнюють 12 см і 18 см, менша сторона дорівнює 6 см. Знайти його більшу сторону.
11. Перпендикуляр, проведений з точки перетину діагоналей ромба до його сторони, поділяє її на відрізки 2 см і 8 см. Знайти діагоналі ромба.
Частина 4
Завдання 12 -13 відкритої форми з розгорнутою відповіддю.
Розв’яжіть завдання та запишіть відповіді.
12. В прямокутний трикутник вписано квадрат так, що у них спільний кут. Катети прямокутного трикутника 6 дм і 8 дм. Знайти сторону квадрата.
13. Бісектриса прямокутного трикутника поділяє гіпотенузу у відношенні 2 : 5. У якому відношенні гіпотенузу поділяє висота?
Контрольна робота № 5
Тема: Подібні трикутники
Варіант 2
Частина 1
Завдання 1 – 8 мають по п’ять варіантів відповідей, з яких тільки ОДНА ПРАВИЛЬНА. Оберіть правильну, на вашу думку, відповідь.