5.8 Значимость оценок параметров регрессии

В предыдущем разделе проверялась гипотеза о значимости вкладов m независимых переменных в дисперсию зависимых переменных. Рассмотрим вклад каждой переменной в построение линии регрессии или значимость каждого параметра регрессии.

Положим параметр регрессии генеральной совокупности. Выдвинем гипотезу H₀: , т.е. оценка параметра регрессии не отличается от истинного значения параметра регрессии; альтернативная гипотеза H₁: , т.е. существует значимая разница между оценкой и истинным значением параметра регрессии. В этом случае мы будем строить двустороннюю критическую область.

Гипотеза H₁ может быть трансформирована в предположение: или . Выбор гипотезы H₁: или гипотезы H₁: зависит от априорных сведений относительно поведения параметра . Тогда для проверки гипотезы H₁: строится односторонняя критическая область, а также для проверки гипотезы H₁: строится тоже односторонняя критическая область.

Из предыдущего видно, что гипотезы H₁, могут быть рассмотрены как односторонние, так и двусторонние гипотезы в зависимости от выдвигаемых предположений относительно параметра .

Если случайная величина имеет нормальное распределение с и дисперсией , значения при фиксированных значениях распределены нормально, то оценки параметров распределены нормально с и дисперсией . В этом случае величина тоже распределена нормально с математическим ожиданием и дисперсией соответственно

, . (5.44)

Однако истинное значение неизвестно и вместо используется оценка . В результате получаем новую статистику

, (5.45)

которая имеет t – распределение с f = n-m-1 степенями свободы, m – количество объясняющих переменных, включенных в регрессию.

В то же время истинное значение тоже неизвестно. Поэтому будем проверять гипотезу H₀: , т.е. выдвигаем предположение о том, что параметр , , не оказывает влияния на поведение линии регрессии.

Для проверки гипотезы H₀: необходимо выбрать уровень значимости . Далее необходимо учесть какова гипотеза Н₁ – двусторонняя или односторонняя, и найти путем расчетов или по таблицам t-распределения соответствующие пороги .

Если , то гипотеза Н₀: , отвергается, т.е. параметр (и его оценка ) оказывает существенное влияние на линию регрессии.

Если , гипотеза Н₀ не отвергается. В этом случае на основе оценок нельзя утверждать о значительном влиянии параметра на линию регрессии. Необходимо пересмотреть вид функции или отказаться от нее.

Положим, гипотеза Н₁ – двусторонняя. Статистика для проверки гипотезы имеет вид

. (5.46)

Ввиду того, что гипотеза Н₁ – двусторонняя, определяется критическое значение (а не ) по t-распределению с n-m степенями свободы. Если гипотеза Н₀ не отвергается.

При проверке значимости оценок параметров регрессии может создаться такая ситуация, что несколько параметров регрессии каждая в отдельности не оказывает существенного влияния на линию регрессии, а в совокупности их влияние существенно. Для разрешения этого вопроса рекомендуется рассчитать коэффициент детерминации с исключенными параметрами [9] и сравнить его с коэффициентом детерминации с не исключенными параметрами.

Предположим, что оценки заданы в виде

(5.47)

и

(5.48)

Регрессия (5.47) содержит m объясняющих переменных, а регрессия (5.48) содержит m₁ объясняющих переменных. Возникает вопрос, есть ли необходимость оценивать дополнительные объясняющие переменные. Эта постановка проблемы эквивалентна проверке гипотезы

H₀: , при альтернативной гипотезе

H₁: .

Для решения этой задачи вычисляются коэффициенты детерминации по объясняющим переменным и по объясняющим переменным соответственно, и используется статистика

, (5.49)

имеющая F-распределение с степенями свободы и степенями свободы. Разность показывает, как влияют на переменную y дополнительные m-m₁ параметров регрессии в совокупности по отношению к той неопределенности, которая заложена в регрессии с m объясняющими переменными. Чем больше разность, тем больше влияние дополнительных параметров регрессии.

По заданному уровню значимости и известным степеням свободы и f₂ находится критическое значение по таблицам распределения Фишера. Критической областью (область отклонения гипотезы Н₀) будут все значения F, удовлетворяющие неравенству . В этом случае следует считать, что дополнительные параметры регрессии оказывают существенное влияние на линию регрессии и ими пренебрегать нельзя.

В противном случае ( ) гипотеза Н₀ не отвергается и параметрами можно пренебречь. Значимость ошибки (вероятность отвергнуть гипотезу Н₀ в то время, как она верна) составляет или в 100 случаях из 100 будет принята гипотеза Н₁, в то время как верна гипотеза Н₀.

Возможна такая ситуация, когда необходимо проверить равенство коэффициентов регрессии в регрессионной модели

,

построенной по выборке . В этом случае выдвигается относительно параметров генеральной совокупности гипотеза Н₀: , против альтернативной гипотезы Н₁: .В данном случае гипотеза Н₁ будет двусторонней гипотезой. Однако, если известны соотношения, что или , гипотеза Н₁ может быть трансформирована в гипотезу Н₁₁: для построения односторонней критической области по заданному уровню значимости, или в гипотезу Н₁₂: для построения односторонней критической области в зависимости от дополнительной информации относительно параметров .

Для проверки гипотезы Н₀ используется статистика [9, стр. 208]

(5.50)

с степенями свободы.

Оценки дисперсий оценок параметров регрессии имеют вид

где – элементы обратной матрицы .

По заданному уровню значимости и числу степеней свободы определяется (в зависимости от типа гипотезы Н₁) критическое значение по таблицам t – распределения. Критическая область (область значений t) определяется неравенством , т.е. если выполняется это неравенство то гипотеза Н₀ отвергается.

Следующий интересный случай, который часто встречается на практике, заключается в следующем.

Исследуются два процесса. Для первого процесса производится выборка объема n₁. Для второго – n₂. Результаты эксперимента и взаимно независимы. По результатам эксперимента строятся две линии регрессии

, ,

отражающие одно и то же физическое явление.

Следует дать заключение - применима ли линия регрессии для описания второго процесса и применима ли линия регрессии для описания первого процесса. По всей видимости, эти линии регрессии и взаимозаменяемы, если их параметры регрессии и соответствующих генеральных совокупностей незначимо отличаются друг от друга. Таким образом, возникает задача проверки нулевой гипотезы Н₀: , против альтернативной гипотезы Н₁: , .

Альтернативная гипотеза Н₁ может быть построена как для двусторонней критической области, так и для односторонней критической области.

Задача проверки гипотезы Н₀ разбивается на несколько этапов.

1. Выдвигается гипотеза Н₀₁: , т.е. остаточные дисперсии двух исследуемых процессов равны.

Альтернативная гипотеза Н₁₁: .

Для проверки гипотезы Н₀₁ используется статистика

, (5.51)

имеющая F – распределение с и степенями свободы. Причем предполагается, что . Если , используется статистика

. . (5.52)

По заданному уровню и степеням свободы и f₂ определяется критическое значение . Если , гипотеза Н₀ отклоняется. Ошибка отклонить правильную гипотезу Н₀ будет в 100 случаях из 100 серий испытаний.

Если гипотеза Н₀ не отклоняется, вычисляется сводная оценка остаточной дисперсии

. (5.53)

2. Второй этап вычислений проводится, если принята гипотеза Н₀, и проверяется гипотеза : , против альтернативной двусторонней гипотезы :

Для проверки гипотезы используется статистика

(5.54)

имеющая t – распределение с f=n₁+n₂-4 степенями свободы.

Оценки дисперсии вычисляются по формуле (5.33).

По заданному уровню значимости и числу степеней свободы f из таблиц t – распределения находится критическое значение порога .

Если , гипотеза Н₀ отвергается и можно утверждать, что разница между и значима.

Если , гипотеза Н₀ принимается и можно утверждать, что расхождение между и незначительно и существующее расхождение определяется шумами измерения. Если хотя бы для одного параметра гипотеза Н₀ отвергается, считается, что генеральная совокупность с параметром для первого процесса не идентична генеральной совокупности с для второго процесса.

Положим, все гипотезы Н₀₁: приняты. Тогда вычисляется оценка коэффициентов регрессии, как среднее взвешенное

(5.55)

В качестве уравнения регрессии по х можно принять величину

, (5.56)

где - средневзвешенная оценка параметра регрессии.

Предложенная методика может быть применена для уточнения параметров регрессии по серии выборок ,..., из одной и той же генеральной совокупности. Серии имеют различные количества наблюдений из-за потери части наблюдений.

Пример 5.1.

П 1. Оценка параметров регрессии

Рассмотрим модель применения регрессионного анализа к восстановлению логистической кривой по экспериментальным данным при , . Логистическая кривая отображена на рисунке П 1 сплошной кривой. Шум имитировался псевдослучайной независимой последовательностью, распределенной по нормальному закону с математическим ожиданием, равным нулю, и с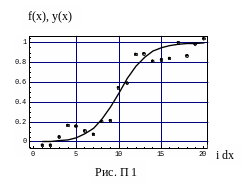 редне квадратичным отклонением, равным 0.08. Выбрано 20 точек отсчета и значения складывались со значениями шума . В результате образовались значения, отображенные на рисунке П 1 точками. Значения результатов эксперимента для полученной реализации приведены в таблице П 5.1.

Таблица П 5.1

x	y(x)	x	y(x)	x	y(x)	x	y(x)
1	-0.03072	6	0.109802	11	0.590109	16	0.840467
2	-0.02847	7	0.081143	12	0.879917	17	0.995829
3	0.052456	8	0.206593	13	0.890103	18	0.866193
4	0.164612	9	0.213295	14	0.815493	19	0.982444
5	0.159817	10	0.546995	15	0.830255	20	1.043403

Положение точек на рисунке П1 зависит от значений реализации шума и может изменяться от эксперимента к эксперименту.

Модель регрессии:

.

В качестве примера выберем функции в виде степенного

ряда¹, наиболее часто применяемого на практике, и остановимся на m=5:

.

В результате регрессионная модель примет вид

.

Коэффициенты регрессии определяются по критерию минимума среднеквадратичной ошибки.

Матрица имеет размерность . Значения функции вычислены в дискретных точках , 0.6

В результате решения системы нормальных уравнений имеем оценки коэффициентов регрессии , которые приведены в таблице П 5.2:

Таблица П 5.2

-0.35296	0.650084	-0.34293	0.077623	-0.007172	0.000231

П о найденным коэффициентам регрессии на рисунке П 2 нанесены точки, вычисленные по кривой регрессии . На этом же рисунке для сравнения изображена кривая f(x).

П 2. Анализ ошибок

2.1 Выборочная дисперсия вычисляется по формуле (5.17) и равна =DY = 0.159084 .

2.2 Оценка дисперсии шума (остаточная дисперсия) производится по формуле (5.22) и равна = 0.0058723.

2.2 Дисперсия , обусловленная регрессией, вычисляется по формуле (5.22) и равна =DY1 = 0.153212.

2.3 Коэффициент детерминации вычисляется по формуле (5.23) и равен Byx = 0.963088.

2.4 Мера неопределённости, содержащаяся в остаточном шуме, вычисляется по формуле и равна Uyx = 0.0369119.

2.5 Запишем ковариационную матрицу , определяющую статистическую связь между параметрами , и вычисленную по формуле (5.32):

2.6 Оценка среднеквадратического отклонения оцениваемого параметра равна корню квадратному от диагональных элементов матрицы , (Таблица П 5.3):

Таблица П 5.3

0.205901	0.301040	0.139341	0.027261	0.002361	0.000074

П 3. Значимость коэффициента детерминации

Проверим гипотезу о том, что коэффициенты регрессии не оказывают влияние на кривую . Значение статистики определяется по формуле(5.43) и равно F= 73.05.

Положим уровень значимости 0.05. Для данного уровня значимости по таблицам распределения Фишера с числом степеней свободы =5 и =14 определим критическое значение .

Из сравнения статистики F и критического значения гипотезу следует отвергнуть, т. е. один или несколько параметров оказывают существенное влияние на функцию .

П 4. Значимость оценок параметров регрессии

Произведем проверку значимости каждого коэффициента регрессии по уровню значимости =0.05. Если коэффициент не влияет на функцию , то можно принять его значение равным нулю. Поэтому проверяется гипотеза : =0, против двусторонней альтернативой гипотезы : 0. Считаем, что распределено по закону Стьюдента с числом степеней свободы, равной n-m-1=14. По таблицам t-распределения определим критическое значение = 1.76131

Статистика для проверки гипотезы имеет вид ,

где - дисперсия, равная диагональным элементам матрицы S.

Ниже приведена таблица П 5.4 значений , , .

Таблица П 5.4

	-0.35296	0.650084	-0.34293	0.07762	-0.007172	0.000231
	0.205901	0.30104	0.13934	0.02726	0.002361	0.000074
	-1.71422	2.15946	-2.46113	2.84742	-3.03727	3.10137

К ак видно из таблицы, для всех значений соблюдается соотношение , то есть гипотеза для этих значений отвергается. Так как , параметр регрессии не оказывает существенного влияния на кривую регрессии и её можно исключить.

На рисунке П 3 изображена кривая y(x) с исключенным коэффициентом . Как видно из этого рисунка, аппроксимация логистической кривой степенным полиномом y(x) дает не очень хорошее приближение. В то же время кривая регрессии y(x) без учета значимости коэффициентов регрессии позволило построить кривую y(x), изображенную на рисунке П4.

К ак видно, эта кривая «ближе» к кривой f(x). Ожидать совпадения кривой f(x) и полинома y(x) не приходится, т.к. даже в отсутствии шума среднеквадратическое приближение полинома y(x) к логистической кривой имеет вид, изображенный на рисунке П 5. Поэтому необходимо более аккуратно подходить к выбору функции .

Пример 5.2.

Рассмотрим сумму двух гармонических сигналов

(П 1)

с параметрами , , 5, 8, , , заданных на интервале наблюдения Т=2. Все величины представлены в относительных единицах. На рисунке П 6 представлена реализация сигнала .

Предположим, амплитуды и фазы составляющих сигнала неизвестны, измерения значений сигнала производятся с интервалом 0.03125 на фоне нормального не коррелированного шума с дисперсией, равной 1. Число точек отсчета 64.

Необходимо по измеренным значениям оценить амплитуды и фазы составляющих сигнала, рассчитать среднеквадратические отклонения оцениваемых параметров и проверить на значимость полученные результаты.

Преобразуем сигнал в форму, удобную для применения регрессионного анализа

. (П 2)

Произведем замену

, , , .

Уравнение регрессии примет вид

, (П4)

где

. (П5)

Коэффициенты регрессии, амплитуды и фазы связаны соотношениями

, . (П6)

Решения нормальных уравнений, оценки среднеквадратических отклонений , оценок и значения статистики при проверке гипотезы : , приведены в таблице П 5.5.

Таблица П 5.5

	0.725655	2.19109	1.90765	3.81343	5.81419
	0.100258	0.141786	0.141786	0.141786	0.141786
	7.23787	15.4535	13.4544	26.8956	41.0066
	0.9221576,	2.468989	2.185544	4.091324	6.09208

Статистика распределена по нормальному закону, так как число точек отсчета достаточно, чтобы применить асимптотические свойства -распределения. Считаем, что математическое ожидание и дисперсия случайной величины равны соответственно и .

Критические значения для проверки двусторонней гипотезы : приведены в четвертой строке таблицы 5. Как видно, все статистики больше критического значения , поэтому гипотеза : , отвергается.

Пользуясь формулами (П6), произведем оценки амплитуды, фазы составляющих сигнала и их среднеквадратические отклонения:

= 0.725655, = 2.90517, = 6.9532, = 41.0441, = 56.7398.

= 0.100258, = 0.37654, = 0.376545, = 7.42623,

= 3.10281.

Из полученных результатов видно, что оценка намного отличается от истинного значения, даже не накрывает истинное значение постоянной составляющей . Это можно объяснить соизмеримостью постоянной составляющей со среднеквадратическим отклонением шума (СКО) =1. Интервалы накрывают истинные значения амплитуд. При оценке фазы истинное значение фазы находится внутри интервала , а фаза не принадлежит интервалу . Объяснить это можно тем, что СКО шума соизмеримо со значениями измеряемых величин, при оценках амплитуд и фаз применяются косвенные методы оценок, мало время наблюдения. Одним из методов уменьшения среднеквадратических ошибок измерений мог бы быть статистическая обработка серий измерений.

Отличительной особенностью примера 5.2 ( по сравнению с примером 5.1) является то, что функции были определены из самой постановки задачи как гармонические функции с известными частотами. В примере 1 функции были взяты произвольно. Дополнительная информация об исследуемом объекте дала возможность получить довольно хорошие результаты в примере 5.2

Приложение

Программа 1

вычисления положительного значения по заданному уровню значимости для левой части неравенства (3.9).

t0= 3.15398 a= 0.05

Из приведенных вычислений для левой границы неравенства рассмотрим для сравнения два значения , превышающее 0.05 и меньшее 0.05.

t0 = 3.1539767000000003, a = 0.05000000362459883

t0 = 3.1539768 a = 0.04999999534904759

Как видно, с точностью до 8-го знака можно взять а=0.05

Программа 2

моделирования процедуры проверки гипотезы о принадлежности двух выборок одной и той же генеральной совокупности

Программа 3

вычисления коэффициента корреляции Спирмена

Программа 4

моделирования регрессионного анализа

для логистической кривой

Аппроксимирующая функция

.

a2=ListPlot[Y,AxesOrigin{0,0},FrameTrue,PlotStylePointSize[0.02],GridLinesAutomatic,DisplayFunctionIdentity];

"R1=Plot[Ww,{x,0,12},PlotRangeAll,FrameTrue,GridLinesAutomatic,

PlotStyleThickness[0.008],DisplayFunctionIdentity];";

Y1=Z.1 ;

"Y1- вектор, оценка значений функции Y по оценкам 1";

U=Table[0,{i,Nn}];"U[[i]]- Остаточный шум";

Do[U[[i]]=Y[[i]]-Y1[[i]],{i,Nn}];

b1=ListPlot[Y1,AxesOrigin{0,0},FrameTrue,PlotStylePointSize[0.02],GridLinesAutomatic,DisplayFunctionIdentity];

b2=ListPlot[Y1,AxesOrigin{0,0},FrameTrue,PlotJoinedTrue,

PlotStyleThickness[0.008],

GridLinesAutomatic,DisplayFunctionIdentity];

Do[Print["Y[",i,"]= ",Y[[i]]," Y1[",i,"]= ",Y1[[i]]," Y0[",i,"]= ",Y0[[i]]," Rn[",i,"]= ",Rn[[i]]" U[",i,"]= ",U[[i]]],{i,Nn}];

Литература

1. Крамер Г. Математические методы статистики, М., Мир, 1975, 648 с.

2. Дунин-Барковский И.В, Смирнов Н.В. Курс теории вероятности и математической статистики, М., Наука, 1965, - 512 с.

3. Кендал М.Дж., Стьюарт А. Статистические выводы и связи. - М.: Наука 1973, 900. с.

4. Большев л.н., Смирнов Н.В., Таблицы математической статистики, М., Наука, 1983, 416 с.

5. Левин Б.Р., Теоретические основы статистической радиотехники, т. 2. М. Сов. Радио, 1968, 504 с.

6. Большев л.н., Об исключении грубых наблюдений.- Теория вероятностей и её применения, 1961, 6, с. 482-484.

7. Пустыльник Е.И., Статистические методы анализа и обработки наблюдений, , М., Наука, 1968, 288 с.

8. Львовский Е.Н. Статистические методы построения эмпирических формул, М., Высшая школа, 1982, 224 с.

9. Фёрстер Э., Рёнц Б. Методы корреляционного и регрессионного анализа. - М.: Финансы и статистика, 1983. 302 с.

10. Кассандрова О.Н. Обработка результатов измерений. - М.: Наука, 1970. 104 с.

11. Поллард Дж. Справочник по вычислительным методам статистики. - М.: Финансы и статистика, 1982. 344 с.

12. Дрейпер Н., Смит Г. Прикладной регрессионный анализ, книга 1. - М.: Финансы и статистика, 1986. 366 с.

13. Дрейпер Н., Смит Г. Прикладной регрессионный анализ, книга 2. - М.: Финансы и статистика, 1987. 351 с.

14. Ивченко Г.И., Медведев Ю.И. Математическая статистика. - М.: Высш. шк., 1984. 248 с.

15. Королюк В.С., Портенко Н.И., Скороход А.В., Турбин А.Ф., Справочник по теории вероятностей и математической статистике.- М.: Наука, 1985.-640 с.

16. Уилкс С. Математическая статистика. – М.: Наука, 1967.-632 с.

17. Леман Э. Проверка статистических гипотез, М. Наука, 1964, 500 с.

18. Дунин-Барковский И.В ,Смирнов Н.В. Теория вероятностей и математическая статистика в технике, М., Изд-во технико- теоретической литературы, 1955, - 556 с.

Оглавление

1. Распределения, связанные с суммой случайных величин 4

1.1 Распределение Стьюдента 4

1.2 Распределение Фишера 9

2. Проверка гипотез 10

3. Отсев грубых измерений 20

3.1 Общие положения 20

3.2 Отсев грубых измерений по малым выборкам 21

3.3 Исключение грубых погрешностей 23

4. Свободные от распределения методы 26

для непараметрических задач 26

4.1 Критерий об однородности двух выборок 27

4.2 Проверка гипотезы о некоррелированности 30

двух распределений 30

5. Регрессионный анализ 37

5.1 Модель регрессии 37

5.2 Анализ ошибок 40

5.3 Дисперсия оценок параметров регрессии 43

5.4 Коэффициент корреляции 44

5.5 Доверительный интервал 45

5.6 Проверка значимости коэффициента корреляции 46

5.7 Значимость коэффициента детерминации 48

Пример 5.1. 54

П 1. Оценка параметров регрессии 54

П 2. Анализ ошибок 57

П 3. Значимость коэффициента детерминации 57

П 4. Значимость оценок параметров регрессии 58

Пример 5.2. 60

Приложение 62

Программа 1 62

вычисления положительного значения по заданному уровню значимости для левой части неравенства (3.9). 62

Программа 2 63

моделирования процедуры проверки гипотезы о принадлежности двух выборок одной и той же генеральной совокупности 64

Программа 3 64

вычисления коэффициента корреляции Спирмена 64

Программа 4 65

моделирования регрессионного анализа 65

Литература 70

11. Экспериментатор может выбрать любую функцию , но при этом он должен обосновать свой выбор.

72