Расчеты на удар при изгибе

На двутавровую балку, свободно лежащую на двух опорах с высоты падает груз (рис. 37, а).

Требуется:

1. Подобрать безопасные размеры сечения балки из условия статического действия .

2. Определить статические напряжения и перемещения в сечении приложения груза .

3. Определить динамический коэффициент при падении груза с высоты .

4. Определить динамические напряжения и перемещения от падающего груза.

5. Заменить одну из опор пружиной с жесткостью и определить динамический коэффициент в этом случае.

6. Определить динамические напряжения и перемещения для балки с пружиной.

7. Сравнить эффективность установки пружины.

8. Сформулировать выводы.

Порядок решения

1. Решаем задачу при статическом действии нагрузки (см. пример 5.10).

2. Подбираем безопасные размеры сечения для статической нагрузки и выписываем из таблицы сортамента его параметры.

3. Определяем истинные (рабочие) напряжения при статическом действии нагрузки.

4. Используя интеграл Мора и способ Верещагина, определяем статические перемещения сечения приложения силы.

5. Определяем динамический коэффициент.

6. Определяем динамические напряжения и перемещения в сечении падения груза.

7. Заменяем одну опору пружиной (демпфером) и решаем задачу заново.

8. Определяем напряжения и перемещения в сечении падения груза на балку с пружиной.

9. Сравниваем обе балки по напряжениям и перемещениям.

10. Формулируем выводы.

Решение

1. Принимае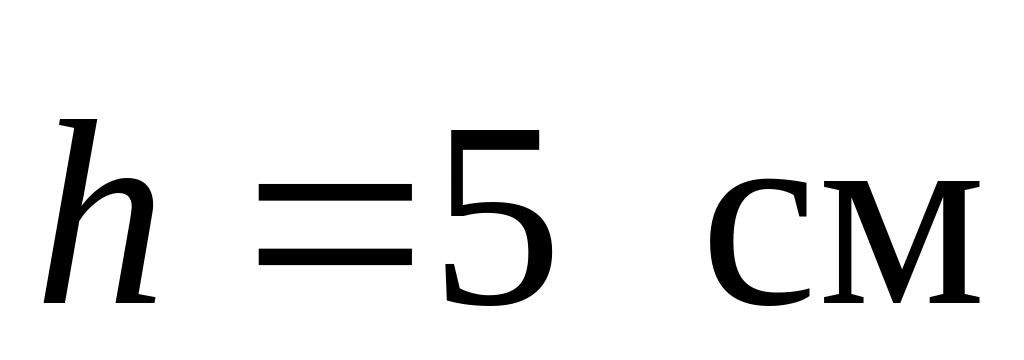м , , ,

м, МПа, МПа.

Схема балки представлена на рис. 37, а.

2. Подбираем безопасные размеры сечения для балки на рис. 37, б.

Из эпюры моментов на рис. 37, в:

.

Из условия прочности балки:

.

Из таблицы сортамента (приложение 1) подбираем двутавр №12, с , .

Расхождение с расчетным значением составит:

– недонапряжение.

3. Фактические напряжения .

4. Для определения статических перемещений приложим в сечении единичную силу и построим эпюру моментов от этой силы (рис. 37, г, д).

По способу Верещагина перемещение сечения будет:

.

5. Определяем динамический коэффициент:

6. Динамические напряжения и перемещения в сечении будут:

,

мм.

Т. к. больше более, чем в 11 раз, то прочность балки не обеспечивается.

7. Для компенсации динамических напряжений введем демпфирующее устройство. Это может быть упругая пружина, амортизатор, рессора или другой упругий элемент. Пусть это будет пружина жесткостью .

Заменим правую опору пружиной (рис. 37, е) и определим статические перемещения сечения с учетом статических и перемещений , при этом:

.

Из рис. 37, е: или

,

.

Новый динамический коэффициент

.

3. Определяем новые напряжения и перемещения для балки с пружиной.

МПа.

мм.

4. Основные рабочие напряжения и перемещения уменьшались в

раза ( раза).

5. Введение упругих элементов в расчетную схему позволяет значительно снизить отрицательное влияние динамических нагрузок (в данном примере в 4,5 раза)

Хотя напряжение в опасном сечении после введения упругих элементов все же получается больше допускаемых ( ), но с учетом коэффициента запаса их влияние скажется на возникновении пластических деформаций только в крайних (периферических) волокнах опасного сечения, тогда как основная часть сечения будет работать в упругой стадии.

Для определения степени опасности кратковременных напряжений найдем предельную нагрузку в опасном сечении по методике, приведенной в примере 5.10.

, где для стали Ст.3.

для двутавра №12 (Табл. приложения).

Изгибающий момент в сечении от действия будет:

Коэффициент запаса по предельным состояниям будет:

Т. о. прочность балки, хотя и с меньшим запасом, но обеспечивается.