5.11. Расчет статически определимой двухопорной балки с консолью

Для двухопорной балки с консолью (рис. 21,а), нагруженной

, , .

Требуется

1. Определить опорные реакции.

2. Построить эпюры поперечных сил и изгибающих моментов .

3. Найти опасное сечение.

4. Подобрать двутавровое сечение балки, обеспечив запас прочности , принять .

5. Используя метод начальных параметров, определить прогибы в характерных сечениях балки и построить ее изогнутую ось. Принять для материала балки (Ст 3) .

6. Факультативно исследовать работу этой же балки по методу предельных состояний и определить запас прочности по сравнению с методом допускаемых напряжений.

7. Сформулировать выводы.

Порядок решения.

1. Используя уравнения равновесия статики, вычислить опорные реакции. Произвести проверку вычислений.

2. Используя метод сечений построить эпюры поперечных сил и изгибающих моментов . Проверить правильность построений.

3. Из условия найти опасное сечение балки.

4. Используя условие прочности, подобрать двутавровое сечение балки и скорректировать запас прочности.

5. Используя универсальное уравнение (метод начальных параметров), определить прогибы характерных сечений балки и построить ее изогнутую ось.

6. Используя метод предельных состояний, исследовать работу балки при развитии пластических деформаций и определить изгибающие моменты начала пластических деформаций 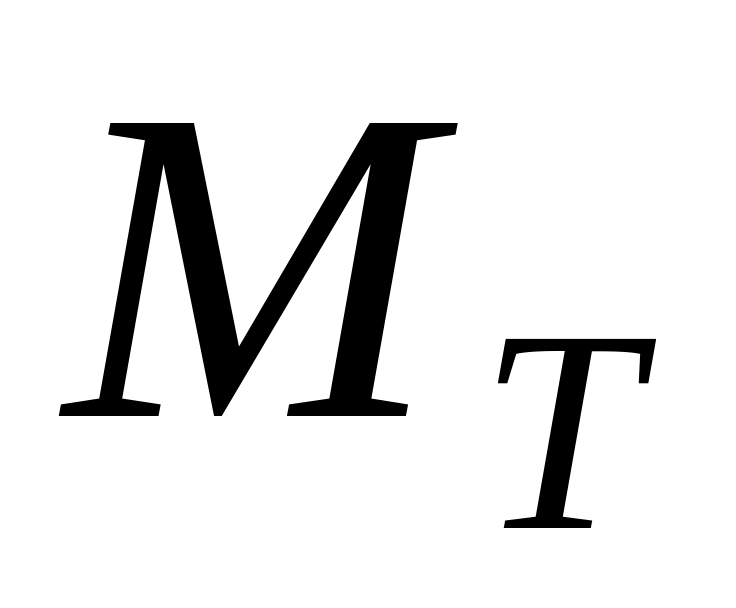и образования пластического шарнира (предельный момент). Определить коэффициенты запаса прочности, сравнивая с и .

7. Сформулировать выводы.

Решение.

1. Определяем опорные реакции.

; .

.

Проверка: или ,

Опорные реакции определены, верно.

2. Балка по характеру приложения нагрузки имеет 3 участка.

На каждом участке выбираем произвольное сечение и вычисляем значения и на каждом участке, используя правило знаков, приведенное в задаче №5, и строим эпюры.

0. Эпюра

. – прямая.

; . , .

. – прямая.

; . , .

. – прямая.

Эпюра представлена на рис. 21, б.

0. Эпюра .

. – парабола.

При , . При , .

При , .

.

– парабола.

При , .

При , .

При , .

В общем случае координата находится из дифференциальной зависимости . В рассматриваемом примере:

; .

. – прямая.

, , , .

Эпюра представлена на рис. 21, в.

3. Из эпюры видно, что в сечении .

Это сечение и будет опасным.

4. Подбираем двутавровое сечение балки на основании п.3 из условия прочности:

; .

.

По таблице ГОСТ находим номер двутавра с ближайшим значением . Это будет двутавр №22 с .

Этот двутавр будет работать с перенапряжением .

Соответственно на 3,2% уменьшится коэффициент запаса и будет равен 1,452 вместо 1,5, что допустимо.

5. Построим изогнутую ось балки, используя универсальное уравнение:

,

где , – координаты приложения сосредоточенной силы и момента,

– координата начала приложения распределенной нагрузки,

– жесткость балки.

В рассматриваемом примере это уравнение примет вид:

Сила приложена в начале координат, нагрузка начинается в начале координат и заканчивается на опоре . Чтобы сохранить единый подход нагрузка продолжается до конца балки, и чтобы расчетная схема не изменилась, от опоры до конца балки прикладывается нагрузка противоположного знака.

Момент приложен на расстоянии от начала координат.

Подставим в универсальное уравнение значение , , , и приведем его к удобному для вычислений виду. Жесткость балки оставим в том же виде.

,

, – прогиб и угол поворота сечения балки в начале координат (начальные параметры).

Из условий закрепления балки при z₁ = 0: – прогиб на опоре , а .

При , – прогиб на опоре . Следовательно:

; Отсюда .

Тогда универсальное уравнение примет вид:

При .

(м).

При , .

При

.

(м).

Если принять (сталь 3).

Для подобранного двутавра №22 .

.

Тогда .

.

Изогнутая ось балки показана на рис. 21, г.