вии с ее размерностью. Измерение основной величины может быть толь­ко абсолютным.

По режиму использования СИТ измерения делят на статические -измерения величины, размер которой можно считать неизменным за вре­мя измерения, и динамические - измерения величины, размер которой нельзя считать неизменным за время измерения.

По количеству наблюдений при измерении различают измерения с однократными и многократными наблюдениями. Многократные наблю­дения, как будет показано далее, дают возможность повысить точность измерения за счет применения статистических методов обработки дан­ных.

В зависимости от достигаемой точности измерения делят на пре­цизионные, контрольно-проверочные и технические.

Первый случай (прецизионные измерения) относится к измерениям при метрологических исследованиях, особо ответственных измерениях, в которых измерения производятся наиболее точно с учетом индивидуаль­ных свойств используемых СИТ и результатов дополнительных измере­ний, выполняемых для контроля условий измерений. В этом случае осу­ществляется апостериорная оценка точности измерений.

Контрольно-проверочные измерения относятся к группе измерений, для которых производится приближенная апостериорная оценка точности.

Технические измерения — наиболее распространенный вид измерений, которые осуществляются с наименьшей точностью, обработка экспери­ментальных данных минимальна, а точность измерений оценивается ап­риорно, в рамках аттестации методики выполнения измерений.

Важнейшим признаком классификации является разделение измере­ний в зависимости от уравнения измерений на прямые, косвенные, совме­стные и совокупные. Для этих видов измерений ниже будут рассмотрены способы обработки их результатов.

1 ПОСТРОЕНИЕ ЭМПИРИЧЕСКИХ ЗАКОНОВ

РАСПРЕДЕЛЕНИЙ И ОПРЕДЕЛЕНИЕ ТОЧЕЧНЫХ

ОЦЕНОК ИХ ЧИСЛОВЫХ ХАРАКТЕРИСТИК

1.1 Основные теоретические сведения

В общем случае результаты измерений (наблюдений) можно считать случайными величинами, учитывая неопределенность взаимного расположения истинного значения измеряемой величины и результата наблюдения. Как и всякая случайная величина, результат измерения полностью характеризуется законом распределения, который получают, обрабатывая результаты многократных наблюдений методами математической статистики. В результате появляется возможность не только оценить характеристики случайной погрешности, но и повысить точность измерения.

1.1.1 Интегральная и дифференциальная функции распределения

Законом распределения случайной величины X называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.

На практике используются так называемая интегральная и дифференциальная функции распределения.

Функцией распределения (интегральной функцией распределения) случайной величины X называется вероятность того, что случайная величина X будет меньше ее аргумента

. (1.1)

Так как вероятность не может быть отрицательной, то . Чем больше х, тем больше вероятность того, что , следовательно , если неубывающая функция. Очевидно, что при , ; а при , (рис. 1.1, а).

Плотность распределения — это вероятность попадания случайной величины X на бесконечно малый интервал .

Из этого определения очевидно, что плотность распределения связана с интегральной функцией распределения соотношением

. (1.2)

Поэтому плотность распределения называют дифференциальной функцией распределения (рис. 1.1,б).

Очевидна и обратная зависимость:

(1.3)

где и — переменная интегрирования, имеющая размерность x.

Отсюда происходит название “интегральная функция распределения”.

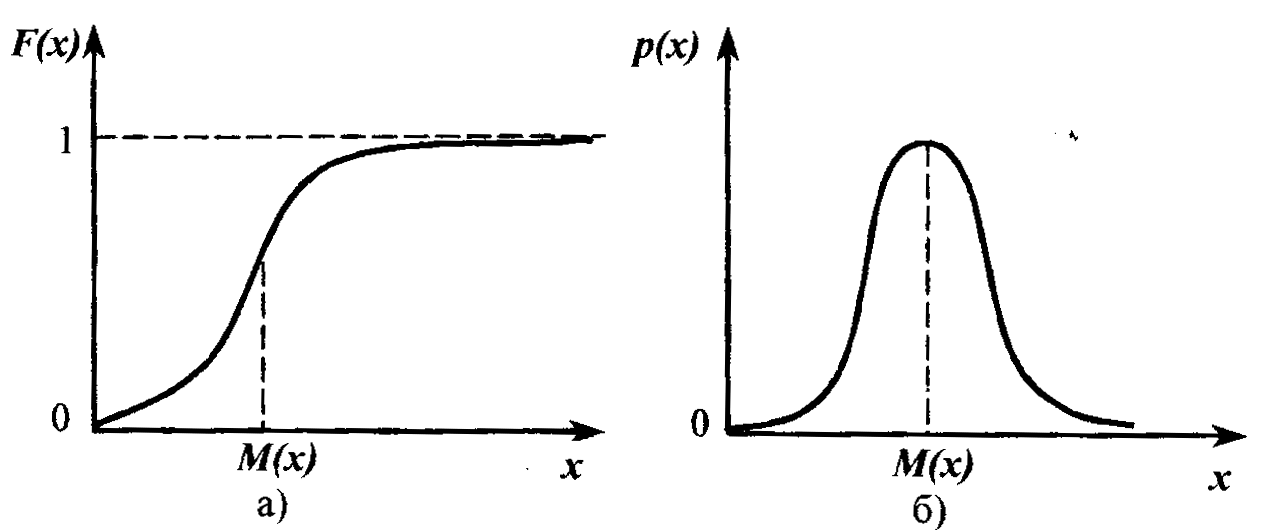
Рисунок 1.1 - Интегральная (а) и дифференциальная (б) функции распределения

Основные свойства плотности вероятности:

1. Плотность вероятности есть неотрицательная функция. Это свойство вытекает из того, что функция распределения есть неубывающая функция.

2. Интеграл в бесконечных пределах от плотности вероятности равен единице (условие нормировки):

Геометрическая интерпретация этого свойства заключается в том, что вся площадь, ограниченная кривой распределения и осью абсцисс, равна единице.

Из определений интегральной и дифференциальной функции распределения видно, что первая из них безразмерна, а вторая имеет размерность, обратную размерности случайной величины.

1.1.2 Кумулятивная кривая и гистограмма

Кумулятивная кривая и гистограмма являются экспериментальными (дискретными) аналогами интегральной и дифференциальной функций распределения, построенными по статистической совокупности из п результатов наблюдений. Результаты наблюдений можно представить на числовой оси в виде точек x₁,x₂,…,x_n. Разность между наибольшим и наименьшим наблюденными значениями отсчетов равна диапазону результатов наблюдения

.

Этот диапазон можно разбить на L интервалов, длительностью

Через границы этих интервалов можно записать формулу для интегральной функции распределения в следующем виде

где j=0,1,…,L i=1,2,…,n

Если m_k — количество наблюденных значений, попавших в k-й интервал, то

Эту зависимость можно представить в виде точек на графике (рис.1.2).

Ломаная линия, соединяющая эти точки, называется кумулятивной кривой.

В пределе, при и кумулятивная кривая стремится к интегральной функции распределения, сохраняя все ее свойства:

1)

2)

3) - возрастающая функция. Также, как интегральная функция распределения связана с дифференциальной, кумулятивная кривая связана с гистограммой:

Эта зависимость представлена на рис. 1.3 и представляет собой совокупность прямоугольников высотой . Гистограмма со­храняет все свойства дифференциального распределения, к которому стремится при и :

1) ;

2) площадь под кривой гистограммы равна 1 (условие нормировки)

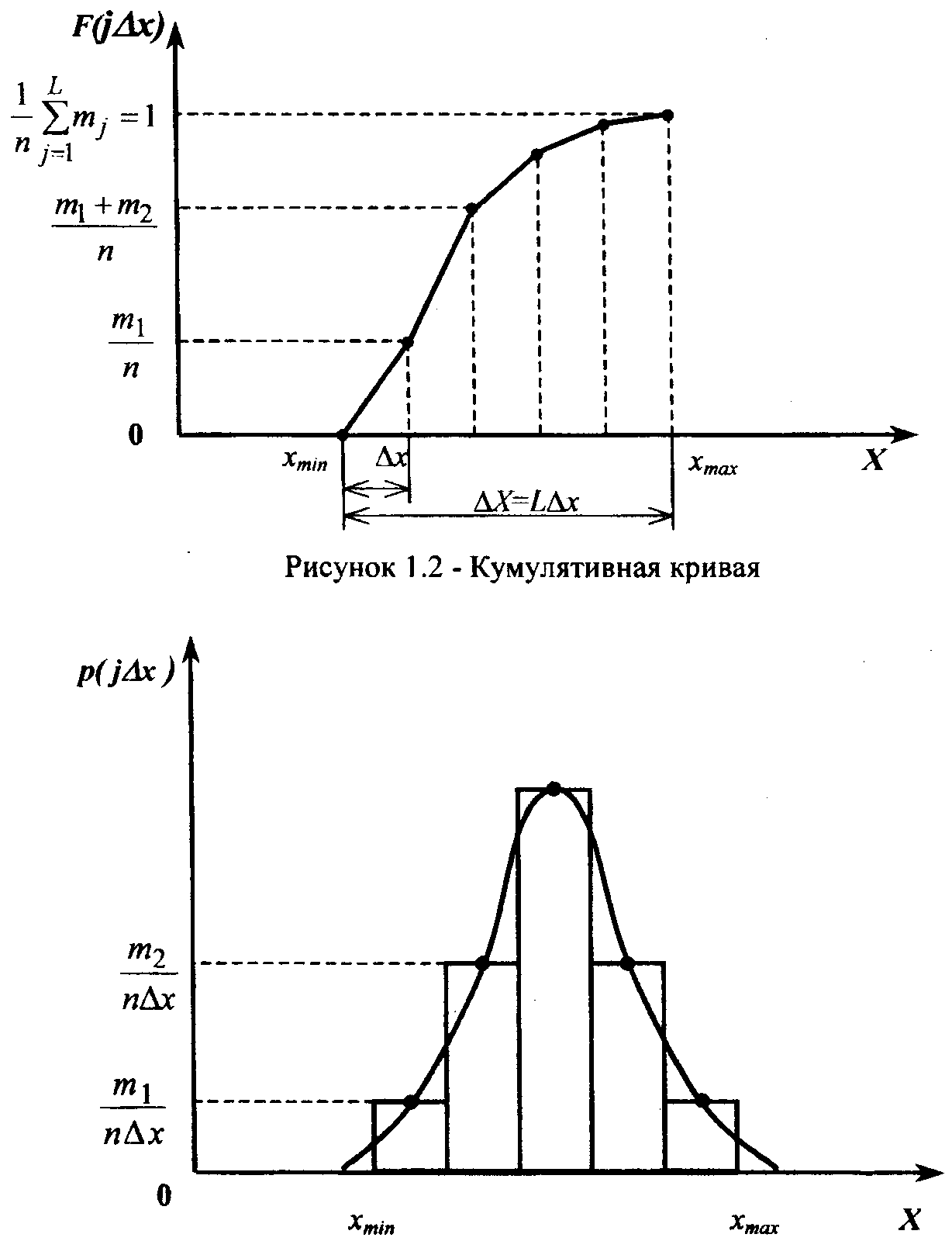
Рисунок 1.2 - Кумулятивная кривая, рисунок 1.3 – Гистограмма

При построении кумулятивных кривых и гистограмм для большей наглядности следует придерживаться следующих правил:

1) интервалы, на которые разбивается ось абсцисс, следует выбирать одинаковыми;

2) число интервалов L устанавливается в соответствии с рекоменда­циями, приведенными в табл. 1.1;

Таблица 1.1

Выбор числа интервалов гистограммы (кумулятивной кривой)

N	40-100	100-500	500-1000	1000-10000
L	7-9	8-12	10-16	12-22

3) масштаб гистограммы (кумулятивной кривой) выбирается таким образом, чтобы ее высота относилась к основанию как 5: 8.

1.1.3 Числовые характеристики случайной величины

Функция распределения полностью описывает случайную величину с вероятностной точки зрения. Однако на практике иногда достаточно указать отдельные параметры, характеризующие распределение случайной величины.

Одними из таких характеристик являются начальные m_k и центральные _k моменты различных порядков k:

(1.4)

(1.5)

Из начальных моментов на практике используется один — начальный момент первого порядка

(1.6)

называемый математическим ожиданием. Математическое ожидание относится к характеристикам положения, указывающим на некоторое среднее значение, вокруг которого группируются все возможные значения случайной величины.

Математическое ожидание, как видно из выражения (1.6), является абсциссой центра тяжести системы материальных точек, расположенных между кривой плотности вероятности и осью абсцисс.

Свойства математического ожидания:

1) математическое ожидание неслучайного числа равно самому это­му числу М (а) =а;

2) постоянный множитель можно выносить за знак математического ожидания М (ах) =а М (х), где a-const;

3) математическое ожидание алгебраической суммы независимых случайных чисел равно алгебраической сумме их математических ожиданий:

M (х+у-z) =M (х) + М (у) -M (z);

4) математическое ожидание произведения независимых случайных чисел равно произведению их математических ожиданий:

М (х*у*z) = M (x) *M (y) *M (z);

5) математическое ожидание отклонения случайного числа от его математического ожидания равно нулю:

М [х-М (х)]=0.

Кроме математического ожидания к характеристикам положения относятся мода и медиана.

Модой называется то значение случайной величины Mod, для кото­рой плотность вероятности имеет максимальное значение (рис. 1.4).

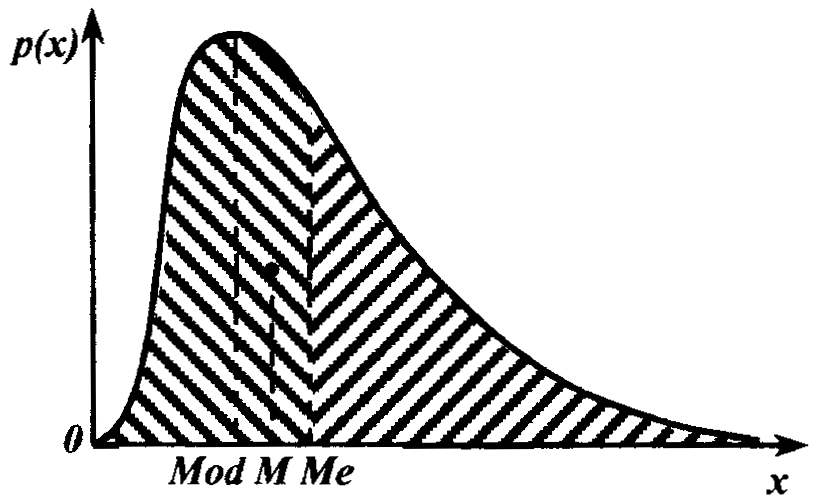
Рисунок 1.4 - Математическое ожидание, мода и медиана распределения случайной величины

Если плотность распределения имеет несколько максимумов, то такое распределение называется полимодальным. Иногда встречаются распределения, мода которых определяет не максимум, а минимум плотности распределения (например — арксинусное, рис. А.1,д). Такие распределения называются антимодальными.

Медианой распределения случайной величины называется такое значение Me, для которого одинаково вероятно, окажется ли случайная величина больше или меньше Me, т. е. Р (х <Ме) =Р (х> Ме). Геометрическая медиана — это абсцисса точки, в которой площадь, ограниченная кривой распределения, делится пополам (рис. 1.4).

В случае симметричного одномодального распределения медиана совпадает с математическим ожиданием и модой.

Из пятого свойства математического ожидания следует, что центральный момент первого порядка равен нулю.

Центральный момент второго порядка, называемый дисперсией D, служит мерой рассеяния случайной величины:

(1.7)

Свойства дисперсии:

1) дисперсия неслучайного числа равна нулю: ;

2) постоянный множитель можно выносить за знак дисперсии, возводя его при этом в квадрат: , где ;

3) дисперсия алгебраической суммы двух зависимых случайных чисел равна

,

где  - коэффициент корреляции

.

4) дисперсия алгебраической суммы независимых случайных чисел равна сумме их дисперсий:

;

5) дисперсия случайного числа равна разности между математическим ожиданием его квадрата и квадратом математического ожидания:

Чем больше дисперсия, тем значительнее рассеяние случайной величины (рис. 1.5).

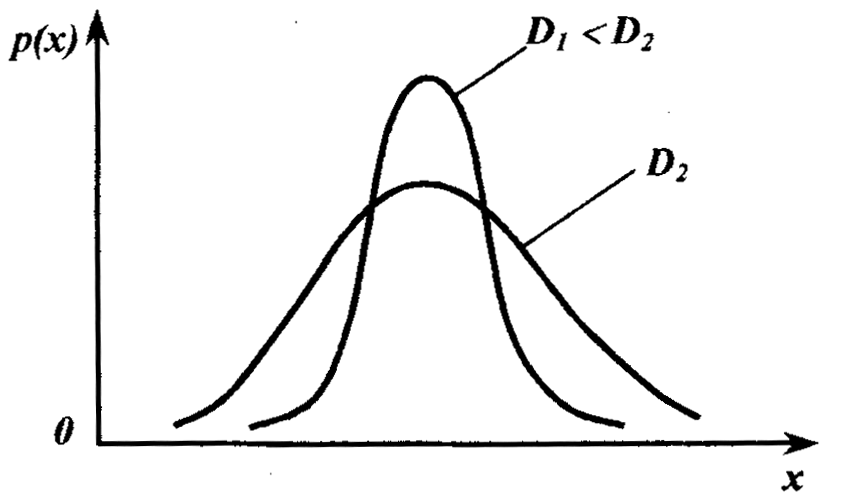
Рисунок 1.5 - Законы распределения случайной величины с различными дисперсиями

В метрологии в качестве меры рассеяния чаще используют среднее квадратическое отклонение (СКО), имеющее размерность случайной величины

(1.8)

Центральный момент третьего порядка является характеристикой асимметрии А:

(1.9)

Асимметрия может быть, положительной и отрицательной. Для симметричных распределений вероятности случайной величины асимметрия равна нулю (рис. 1.6).

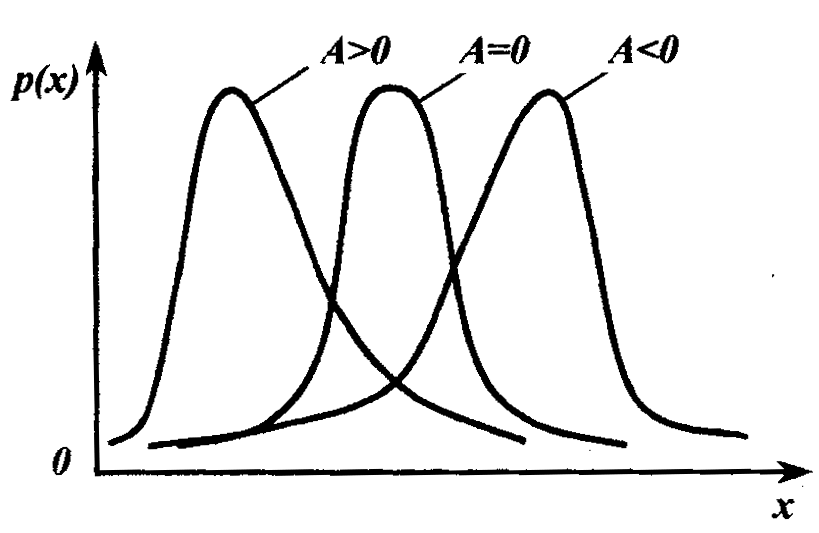
Рисунок 1.6 - Законы распределения с различной асимметрией

Четвертый центральный момент используется для оценки островершинности дифференциальной функции распределения вероятности. Мерой островершинности является эксцесс

(1.10)

В выражении (1.10) вычитание тройки производится для того, чтобы сделать эксцесс равным нулю для нормального закона распределения, для которого .

Таким образом, эксцесс у законов распределения вероятности будет близок к нулю, если их кривая плотности распределения будет иметь колоколообразную форму. Кривые с более острой вершиной имеют положительный эксцесс, а с более пологой — отрицательный (рис. 1.7).

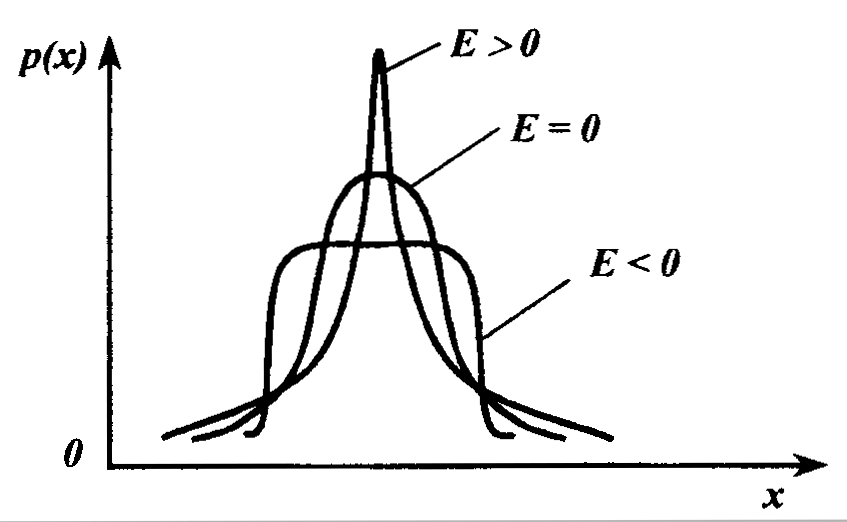
Рисунок 1.7 - Законы распределения с различным эксцессом