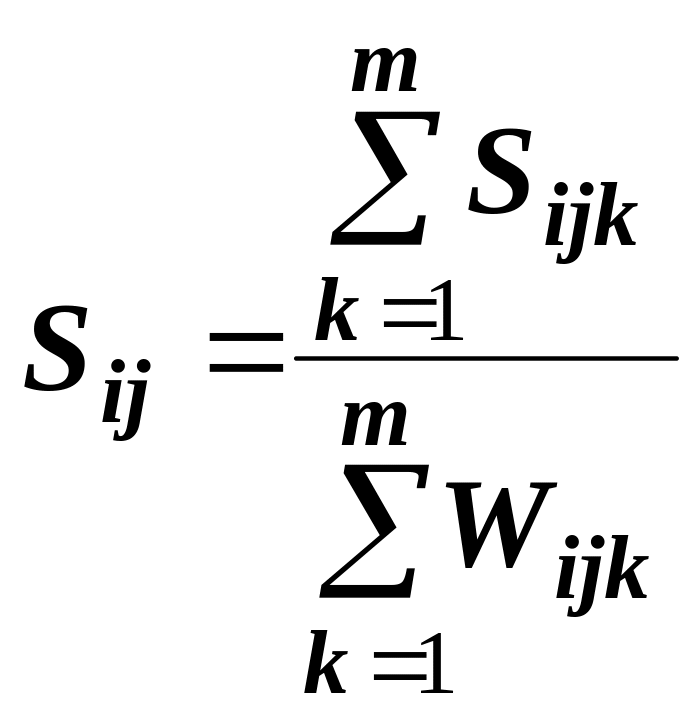Примеры мер различия и сходства, используемых в кластерном анализе эмпирических данных

Мера различия или сходства	Формула для вычисления	Ссылки
Euclidean distance (Евклидово расстояние)		[3. С.212; 17. С.576; 19. С.87]
City-block distance, Manhattan distance, Block distance (Расстояние «городских кварталов», сити-блок, Манхетен)		[17. С.577; 19. С.87]
Power distance, Minkowski distance (Степенное расстояние; метрика Минковского)		[5. С.158; 17. С.576]
Gower coefficient (Коэффициент Гауэра)		[5. С.160-164; 17. С.290-294]

Обозначения:

- объекты из эмпирической выборки данных;

- значение меры различия d для объектов и ;

- значение меры сходства s для объектов и ;

- результаты измерения k-того признака у объектов и ;

m - количество измеряемых признаков;

r - степенной параметр метрики Минковского;

- соответственно, значение вклада в меру сходства между объектами и измерения по k-тому признаку, а также приписываемый этому вкладу «вес», зависящий от характера измерительной шкалы данного признака.

Каждая из мер, представленных в табл. 11.2-3, имеет свое назначение, область и особенности применения:

• Евклидово расстояние является в кластерном анализе наиболее популярной метрикой; для трехмерного пространства оно совпадает с обычным «обыденным» расстоянием. Хотя евклидова метрика ориентирована, в первую очередь, на применение к данным, измеренным в шкалах интервалов или отношений, но на практике она часто применяется (хотя и не всегда корректно) и для данных, полученных в других шкалах. Евклидову метрику целесообразно применять для переменных, измеренных в одних и тех же единицах (или для нормированных данных); в противном случае целесообразно использовать нормированный вариант евклидовой метрики [3. С.212]. Обсуждение проблем применения евклидовой метрики имеется, например, в работах [5. С.157; 21. С.66].

• Расстояние «Манхетен» часто применяется для номинальных и дихотомических признаков [3. С.212]. Это расстояние равно сумме покоординатных различий между точками (иногда эту сумму делят на число координат, и тогда получается среднее покоординатное различие). Это расстояние во многом аналогично евклидовой метрике, однако при его применении сглаживается эффект больших различий по отдельным координатам (так как эти различия, в отличие от метрики Евклида, не возводятся в квадрат). Обсуждение данной метрики имеется в [5. С.158; 17. С.577; 19. С.87].

• Метрика Минковского; включает определяемый исследователем параметр r является обобщением случаев евклидова расстояния (r=2), метрики Манхетен (r=1) и некоторых других метрик. В силу этого данную метрику удобно использовать при экспериментах с расстоянием, гибко варьируя ее параметр. Обсуждение метрики Минковского имеется, например, в [5. С.158; 17. С.576].

• Коэффициент сходства Гауэра предназначен для решения задач, в которых одновременно используются признаки, измеренные в различных шкалах: интервальных, порядковых и дихотомических. В этом - его несомненное преимущество, тем более, что мер сходства для работы со смешанными шкалами относительно немного. К сожалению, коэффициент Гауэра редко используется в психологических исследованиях и не реализован в рассматриваемых статистических пакетах, поэтому методика его вычисления будет подробно рассмотрена нами при решении задачи 11.5-4. Обсуждение этого коэффициента имеется в [5. С.160-164; 17. С.290-294].

Кроме представленных в табл. 11.2-3, в кластерном анализе применяется множество иных мер сходства или различия:

• Для интервальных данных - расстояния Squared Euclidean (Квадрат евклидова), Chebychev (Чебышева), Mahalanobis (Махаланобиса); мера близости Pearson correlation (Коэффициент корреляции Пирсона) и другие. На практике многие из этих мер применяются, хотя и далеко не всегда обоснованно, к данным, измеренным в неинтервальных шкалах.

• Для порядковых данных - Chi-square measure (Мера хи-квадрат), Phi-square measure (Мера фи-квадрат), меры близости – коэффициенты ранговой корреляции Spearman (Спирмена), Kendall (Кендалла), Чупрова и другие.

• Для номинальных и двоичных (дихотомических) данных - Variance (Рассеяние), Dispersion (Дисперсия); коэффициенты Hamming (Хемминга), Phi 4-point correlation (Четырехпольный коэффициент корреляции фи), Lambda (Ламбда), Anderberg’s D (D Андерберга), Jaccard (Джаккарда), Kulczynski (Кульчицкого), Lance and Williams (Ланса и Уильямса), Ochiai (Очиаи), Rogers and Tanimoto (Роджерса и Танимото), Russel and Rao (Русселя и Рао), Sokal and Sneath (Сокала и Снита), Yule’s Y (Коэффициент Юла Y), Yule’s Q (Коэффициент Юла Q) и другие.

• Для данных, измеренных в смешанных шкалах, применяются меры близости Журавлева, Воронина, Миркина и другие.

Итак, выбор конкретной меры различия или сходства определяется не только (и не столько) субъективным предпочтением исследователя, сколько объективными свойствами исследуемого явления, в частности, характером используемых измерительных шкал.

Подробнее вопрос о мерах различия и сходства при кластерном анализе рассмотрен в работах [2; 3-5; 9; 17; 22; 23; 26; 35].