11.2. Классификация методов кластерного анализа по измерительным шкалам, направлению кластеризации и используемой метрике

Первые три этапа процедуры кластеризации целесообразно рассмотреть совместно, так как и в теории, и, тем более, на практике они тесно взаимосвязаны между собой.

Получение исследователем выборки эмпирических данных, представляющих собой результаты измерения ряда признаков (например, характеристик психических процессов, состояний, свойств)

, выполненного у некоторой совокупности объектов (например, респондентов) , с необходимостью предполагает

наличие определенных измерительных методик. Согласно этим методикам результаты измерения могут быть представлены в измерительной шкале того или иного типа (номинальной, порядковой, интервальной, отношений). Как и во многих других случаях, предпочтительными с точки зрения математических оснований здесь являются интервальные шкалы и шкалы отношений, но, в то же время, в кластерном анализе, в отличие, например, от факторного, дискриминантного или дисперсионного анализа, требования к типу шкалы являются не такими жесткими: они, скорее, влияют на выбор конкретного метода кластеризации, а не на принципиальную допустимость кластеризации как таковой.

Нередко в психологических исследованиях результаты измерения различных признаков получают в шкалах разных типах: например, часть признаков измерена в интервальной шкале, а другая часть – в номинальной. В подобных случаях наличия смешанного типа шкал вопрос о выборе подходящего метода кластеризации должен решаться с большой осторожностью. Теоретические основы использования в кластерном анализе смешанных шкал исследованы недостаточно, поэтому велика опасность получения некорректных результатов. Наиболее надежными выходами из данной ситуации являются следующие возможности:

• вполне корректным здесь будет применение метода, предназначенного для самого низшего из имеющихся типов шкал (в приведенном примере – для номинальной), однако для использования подобных методов иногда необходимо соответствующим образом преобразовывать результаты, полученные в шкалах более высокого уровня;

• можно на последующих этапах процедуры кластеризации выбрать метрику (меру расстояния), специально предназначенную для шкал смешанного типа, однако набор таких метрик весьма ограничен и применяются они относительно редко;

• и, наконец, наиболее простой путь – стремиться избегать использования шкал разного типа при получении данных, предназначенных для кластеризации.

Итак, все методы кластеризации теоретически можно было бы разделить на виды по типу измерительной шкалы, в которой получены эмпирические данные, различая, например, методы, предназначенные для интервальных, порядковых и номинальных шкал. Однако такое деление было бы преждевременным, так как сам по себе тип шкалы еще не определяет характера всей процедуры кластеризации в целом. Точнее, использованные при получении эмпирических данных измерительные шкалы влияют на выбор подходящего метода кластерного анализа не прямо, а косвенно – через выбор метрики необходимого для осуществления кластеризации метрического пространства, обсуждаемый ниже.

Полученные эмпирические данные должны быть представлены в виде матрицы «объект – признак», то есть прямоугольной таблицы чисел, строки которой соответствуют измеренным объектам (например, респондентам), а столбцы – измеряемым признакам (например, характеристикам психических процессов, состояний или свойств). Исследователь сначала заносит полученные данные в таблицу «объект-признак», общий вид которой показан в табл. 11.2-1. Матрица «объект-признак» будет отличаться от таблицы «объект-признак» только тем, что в матрице явно не присутствуют заголовки строк и столбцов. Таким образом, таблице 11.2-1 будет соответствовать матрица «объект-признак» (в фундаментальном справочнике [9. С.143] – матрица «объект-свойство»), имеющая размеры , (то есть, в общем случае, прямоугольная), обозначенная через и приведенная в формуле 11.2-1.

Таблица 11.2-1

Общий вид таблицы «объект-признак»

Признаки Объекты	X1	X2	…	Xj	…	Xm
A1	a11	a12	…	a1j	…	a1m
A2	a21	a22	…	a2j	…	a2m
…	…	…	…	…	…	…
Ai	ai1	ai2	…	aij	…	aim
…	…	…	…	…	…	…
An	an1	an2	…	anj	…	anm

. (11.2-1)

При построении матрицы «объект – признак» нередко возникает серьезная проблема, связанная с тем, что признаки рассматриваемых объектов могут оказаться измеренными в разномасштабных единицах измерения: в этом случае для адекватного определения расстояния между объектами целесообразно применить нормирование показателей, переводящее их в безразмерные величины (или к единому общему масштабу). Нормирование представляет собой переход к некоторому единообразному описанию для всех признаков, к введению новой условной единицы измерения, допускающей формальные сопоставления объектов. Наиболее распространенные способы нормирования показателей (переход от исходных значений a к нормированным значениям z) представлены в табл. 11.2-2.

Таблица 11.2-2

Способы нормирования исходных данных

№ п/п	Формула нормирования	Допустимые шкалы	Особенности
1		Интервалов, отношений
2		Отношений
3		Отношений
4		Отношений
5		Интервалов, отношений

Обозначения:

- нормированное значение элемента матрицы «объект-признак»;

- среднее значение элементов по –тому столбцу матрицы «объект-признак» (другими словами – среднее значение измеренного признака по всем подвергнутым измерению объектам ;

- среднее квадратическое отклонение, вычисленное по –тому столбцу матрицы «объект-признак» (среднее квадратическое отклонение значений признака );

, , - соответственно, наибольшее, наименьшее и некоторое эталонное (нормативное) значение признака .

Ясно, что распространенные способы нормирования применимы лишь к данным, полученным в шкалах интервалов и отношений. Применение этих способов к номинальным или порядковым данным является некорректным. Для таких шкал нормирование обычно не проводится, однако в качестве «компенсации» выбираются соответствующие адекватные меры различия или сходства, рассматриваемые ниже. Кроме того, заметим, что приведенные в табл. 11.2-2 способы нормирования выполняются «по столбцу», однако, при необходимости аналогичное нормирование можно выполнить «по строке».

Более подробную информацию о проблеме нормирования показателей при построении матрицы «объект-признак» можно получить в [4. C.27-28], где имеются ссылки на дополнительные источники.

Далее необходимо представить данные в виде точек многомерного пространства, снабженных соответствующим набором координат. Для этого, в первую очередь, исследователю надо принять решение о направлении кластеризации, то есть о том, что именно будет подвергаться разделению на кластеры: объекты (случаи), признаки (измеряемые переменные), или и то, и другое одновременно. В психологических исследованиях часто встречается и кластеризация объектов, и кластеризация признаков; третий вариант (одновременная кластеризация и объектов, и признаков) используется сравнительно редко и не будет рассматриваться в пособии; прочитать о нем можно в работе автора этого подхода Дж.А.Хартигана (G.A.Hartigan) [41].

После принятия решения о направлении кластеризации исследователь получает возможность представить эмпирические данные в виде элементов (точек) некоторого многомерного пространства. В соответствии с альтернативой решения о направлении кластеризации (объекты или признаки) возможное представление выборки также двойственно, так как ее можно представить следующими способами:

• Как набор из n точек , имеющих координаты , где каждое число есть результат измерения i-того объекта по j-тому признаку. Другими словами, в таком представлении точки – это объекты; каждый из них имеет столько координат, сколько измерялось признаков; каждая точка соответствует одной строке матрицы «объект-признак».

• Как набор из m точек , имеющих координаты , где каждое число есть результат измерения j-того признака у i-того объекта. Здесь точки – это признаки, и каждый из них имеет столько координат, сколько измерялось объектов; при этом каждая точка соответствует одному столбцу матрицы «объект-признак».

Вопрос о том, как именно представлять эмпирические данные, решает исследователь, исходя из поставленной цели. В зависимости от его решения образуемое для представления данных метрическое пространство будет иметь размерность: равную либо n - числу объектов, либо m - числу подвергаемых измерению признаков каждого объекта. Никаких принципиальных различий в самой процедуре для вариантов кластеризации объектов или признаков нет: для кластерного анализа, в определенном смысле, «все равно» что именно подвергать классификации: объекты (респондентов) или признаки (свойства). При последующем обсуждении для определенности будем считать, что исследователя интересует кластеризация объектов (случаев).

Полученное таким образом многомерное пространство эмпирических данных для осуществления возможности кластеризации необходимо превратить в метрическое: построение метрического пространства предполагает не только задание координат точек, но и выбор расстояния между ними (метрики). Таким образом, понятие метрического пространства неразрывно связано с понятиями пространства и метрики. Рассмотрим эти понятия.

В математике известно, что понятие пространства, как и понятие множества, являются наиболее базовыми, фундаментальными, и поэтому не имеют точного и математически строгого определения; считается, что эти понятия доступны нам на интуитивном уровне. С учетом этого обстоятельства, пояснить (а не определить) понятия множества и пространства можно следующим образом: под множеством понимается совокупность (конечная или бесконечная) некоторых объектов произвольной природы (людей, точек, чисел и т.д.). В свою очередь, пространство – это некоторое множество объектов, для которой заданы какие-либо структурные свойства (например, взаимная упорядоченность объектов или другие взаимосвязи между ними).

Приняв понятия множества и пространства на интуитивном уровне, мы можем уже более строго дать следующее определение: метрическим пространство – это пространство, состоящее из некоторых объектов, называемых точками (или элементами) данного

пространства (в нашем случае ), между которыми

задана функция расстояния , называемая метрикой, определенная на всех упорядоченных парах точек множества и удовлетворяющая

следующим условиям для любых элементов :

Неотрицательность: . (11.2-2)

Рефлексивность: . (11.2-3)

Симметричность: . (11.2-4)

Транзитивность: . (11.2-5)

Нередко при применении кластерного анализа, особенно в области психологии, эти требования к расстоянию ослабляют, отказываясь от некоторых из них: чаще всего - от транзитивности («неравенства треугольника»), или симметричности. В этом случае мы имеем дело уже не с «настоящей» метрикой, а с «ослабленной» (так как для нее выполняются не все фигурирующие в определении требования). Такие меры различия получили название псевдометрик, а конструируемое с их помощью пространство, соответственно, называется псевдометрическим. Подробное рассмотрение их особенностей выходит за рамки данной работы, поэтому в дальнейшем изложении, говоря о мерах различия, мы не будем различать метрики и псевдометрики, а также метрический или псевдометрический статус пространства. Дополнительную информацию об особенностях использовании псевдометрик в кластерном анализе можно получить в источниках [9; 22; 23; 28; 34; 35; 39].

Выбрав меру различия, исследователь получает возможность перейти от матрицы «объект-признак» (см. формулу 11.2-1) к матрице попарных расстояний между эмпирическими точками (в рассматриваемом случае – между объектами) построенного метрического пространства, представленной следующим соотношением:

. (11.2-6)

Матрица попарных расстояний имеет следующие особенности:

• она – квадратная (то есть число строк в ней равно числу столбцов) и имеет; в рассматриваемом случае, размеры ;

• любой элемент этой матрицы представляет собой расстояние между точками с номерами 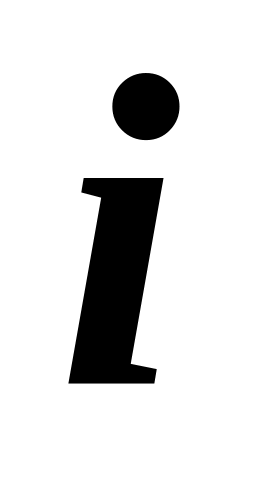и пространства данных;

• она симметричная, так как по свойству симметричности расстояния 11.2-4 для любых элементов и ;

• на ее главной диагонали стоят нули, так как по свойству рефлексивности расстояния 11.2-3 для любого номера .

Получив матрицу расстояний, можно перейти к последующим этапам процедуры кластеризации. Но во многих статистических пакетах вместо матрицы «объект-признак» можно изначально использовать в качестве входных данных процедуры кластеризации предварительно построенную матрицу расстояний.

В предыдущем изложении мы опирались на понятие меры различия (расстояния, метрики), однако, возможен альтернативный подход к постановке задачи кластеризации, основанный на мере сходства (близости, похожести, подобия, толерантности) элементов метрического пространства. В математическом плане эти подходы эквивалентны, то есть приводят к одинаковым результатам кластеризации. Конкретный выбор одного из этих двух подходов часто определяется содержательным смыслом исследуемых явлений.

При одной и той же глобальной стратегии кластеризации могут использоваться различные меры различия или сходства. Отдельные примеры мер различия и сходства приведены в табл. 11.2-3.

Таблица 11.2-3