Розв’язання

Для обчислення площі перейдемо до полярних координат, поклавши , .

Отримаємо: ,

,

.

Так 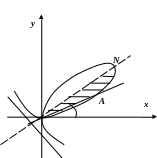як при заміні на , а на рівняння на змінюється, то крива симетрична відносно прямої . Тому шукану площу можна розглядати як подвоєну площу . При цьому радіус-вектор повертається від початкового положення на кут . Отже,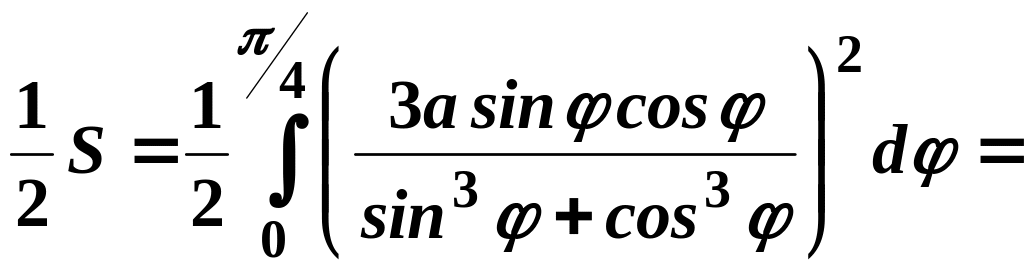

.

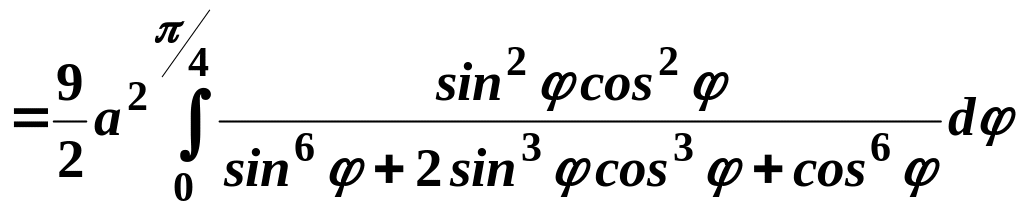Винесемо в знаменнику за дужки:

.

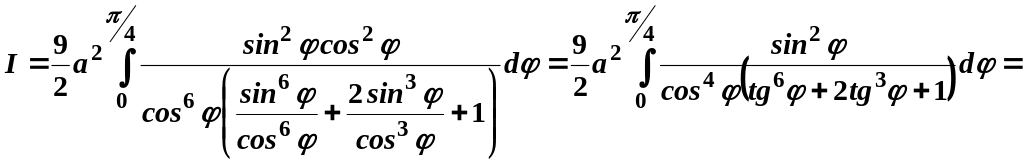
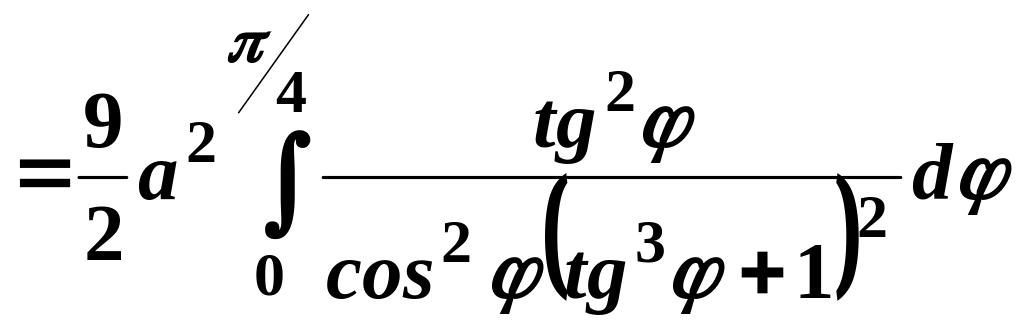Зробимо заміну , .

Нові межі інтегрування: , .

Отже, .

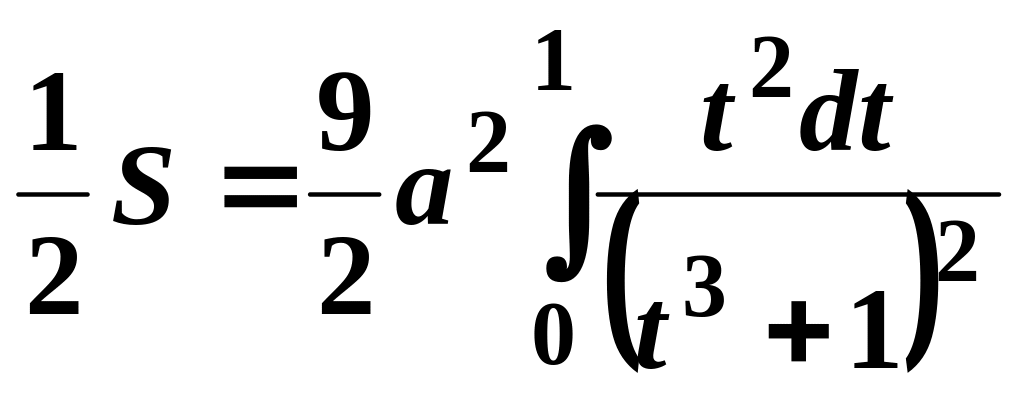Ще раз зробимо заміну , , , .

Тоді: .

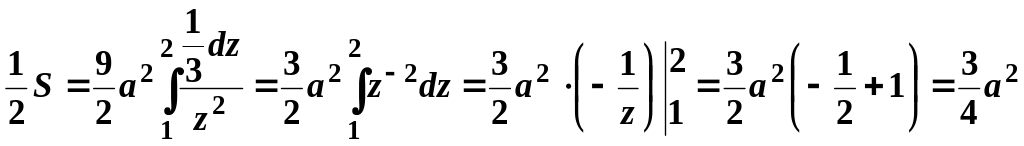Отримаємо: кв. од.

Завдання для самостійної роботи

Обчислити площі фігур, обмежених лініями:

1. , ;

2. , , , ;

3. , ;

4. , , ;

5. , , ;

6.

7.

8. , ;

9. .

Обчислити площу фігури, обмеженої лініями.

1. , Відповідь. .

2. , Відповідь. .

3. Відповідь.

4. , Відповідь. .

5. , Відповідь. .

§ 2. Означення неперервної кривої. Спрямлювана крива. Застосування визначеного інтеграла до обчислення довжини плоскої кривої.

Нехай плоска крива А˘В (рис.1)

задана параметрично х = х(t), у = у(t), α ≤ t ≤ β, де х = х(t), у = у(t) – неперервні функції на відрізку [α; β], причому точка А відповідає значенню параметра

t = α, а точка В – значенню параметра t = β.

Розібємо відрізок [α; β] на n частин точками

α = t₀ < t₁ < … < t_к < t_{к + 1} <…< t_n = β .

Сукупність точок t_0, t_1, t_n називатимемо Т – розбиттям відрізка [α; β]. Кожному значенню параметра t = t_n, k = 0, 1, …,n – 1, на кривій А˘В відповідає точка М_к. Сполучимо ці точки відрізками прямої. В результаті дістанемо, що в криву А˘В вписано ламану лінію. Позначимо периметр цієї ламаної лінії через

Р = М_к М_к+1.

Зрозуміло, що периметр Р залежить від розбиття Т:

Р = Р(Т).

Найбільшу довжину частинного відрізка [t_К; t_к+1] позначимо через

λ(Т) = mах(t_к+1 - t _к ). Якщо λ(Т) → 0, то внаслідок неперервності функцій

х = х(t), у = у(t) найбільша довжина сторонни ламаної також наближатиметься до нуля.

Означення 1.Число S називають границею периметра Р = Р(Т) ламаної лінії, вписаної в криву А˘В при λ(Т) → 0, якщо для будь – якого ε > 0 існує число

δ >0, яке не залежить від розбиття Т і таке, що як тільки λ(Т) <δ, то

|Р(Т) - S| <ε

і позначають

S = Р(Т).

Означення 2.Якщо існує границя периметра ламаної лінії, вписаної в кривуА˘В при λ(Т) → 0, то криву А˘В називають спрямлюваною, а саму границю (число S) називають довжиною дуги кривоїА˘В.

Зауважимо, що це означення стосується незамкнених кривих (точка А не збігається з точкою В).

Обчислення довжини дуги плоскої кривої

Нехай крива задана рівнянням , , причому неперервна разом із своєю похідною на . Тоді довжина дуги кривої визначається формулою

. (27.7)

Вираз називається диференціалом дуги. В разі, коли крива задається рівнянням довжина дуги кривої обчислюється так:

. (27.8)

У разі параметричного задання кривої , довжина дуги дорівнює:

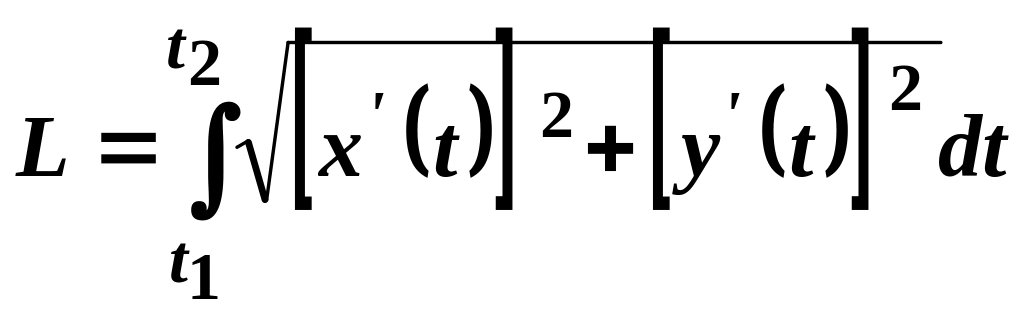. (27.9)

Якщо ж гладка крива задана рівнянням в полярних координатах, то

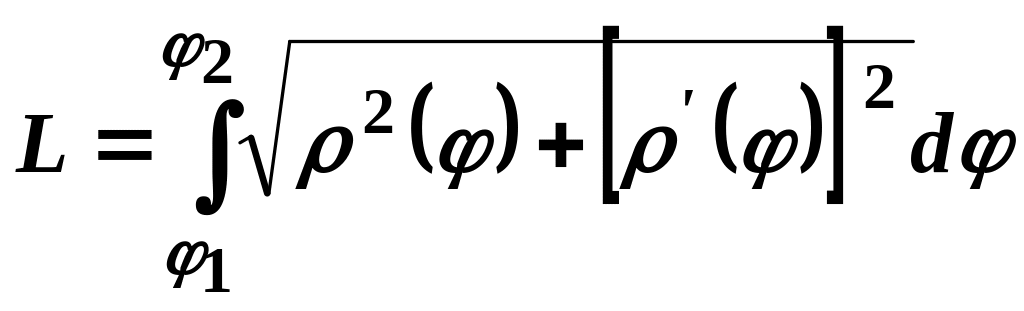. (27.10)