§ 4. Оцінка інтегралів. Формула середнього значення.

1⁰. Якщо на відрізку [а;b] функція то (1)

▲ Дійсно, інтегральна сума від функції на [а;b] невід’ємна, так як i=1,2,3,…,n. Прийшовши до границі при в нерівності , одержимо

геометрично твердження очевидне.

2⁰. Якщо всюди на [а;b] , то

▲ Застосовуючи оцінку 1⁰ до функції маємо

За властивістю 6⁰ з § 3 маємо звідки одержуємо

3⁰. Якщо m і M відповідно найменше і найбільше значення функції на відрізку [а;b], а<b, то ▲ є [а;b] маємо

Застосовуючи оцінку 2 і зінтегрувавши ці нерівності, одержимо

і тоді

4⁰. Теорема (про середнє)

Якщо функція неперервна на відрізку [а;b] то на [а;b] така точка , що

(*)

▲ Так як - неперервна то за теоремою Вейєрштрасса існують числа m і M такі, що

Згідно оцінки 3⁰ звідси маємо

і отже 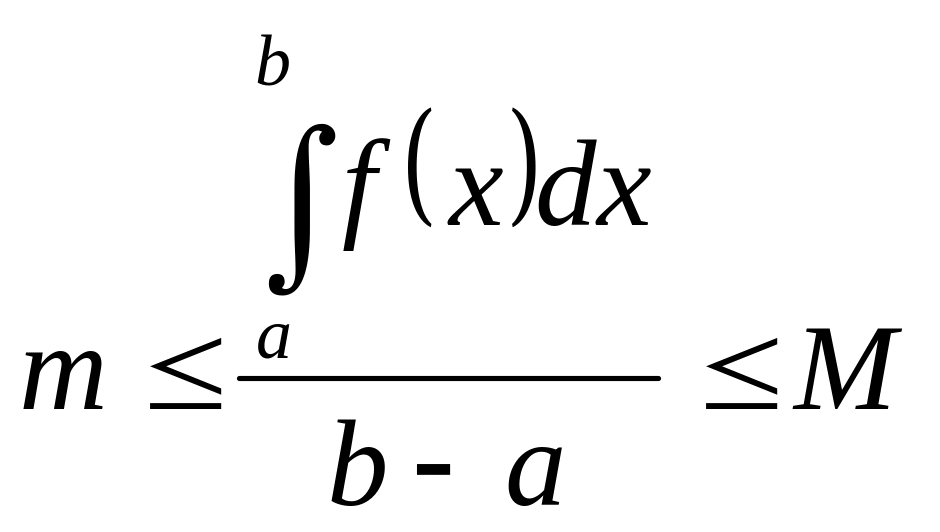покладемо

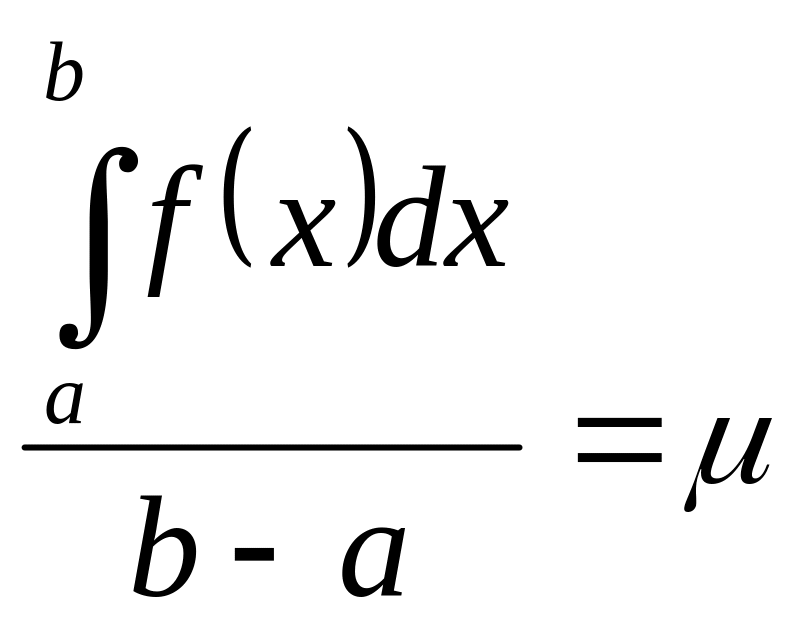
Так як знаходиться між найменшим та найбільшим значенням неперервної функції y= на відрізку [а;b], то за відомою теоремою про походження функції через проміжне значення, існує точка така, що , тому 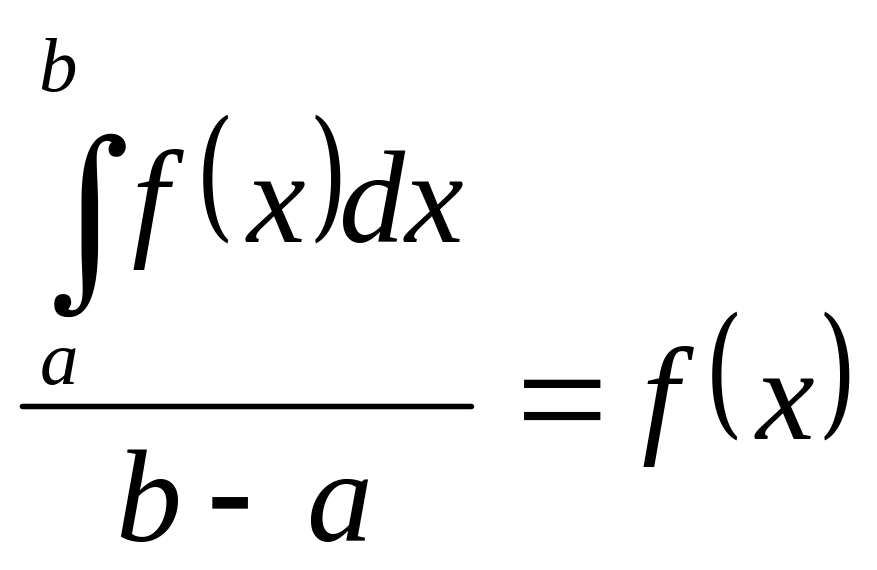, а це рівносильно рівності (*). Величина в формулі (*) називається значенням функції на відрізку [а;b].

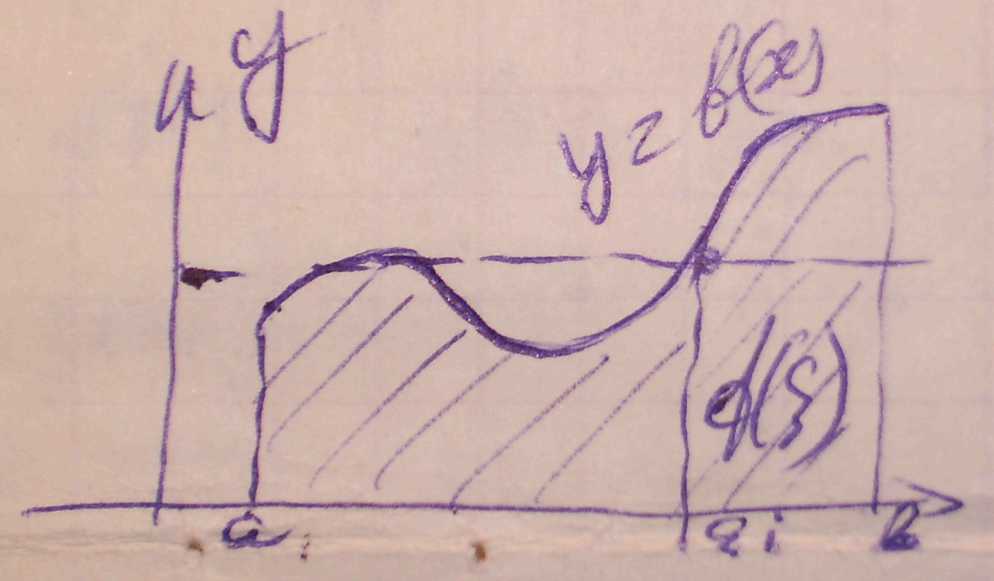
Примітка. Геометричний зміст теореми про середнє.

Величина визначеного інтеграла при дорівнює площі прямокутника, що має висоту і основу b-a.

Лекція № 26

Тема: Інтеграл із змінною верхньою межею. Формула Ньютона - Лейбніца. Заміна змінної у визначеному інтегралі. Формула інтегрування частинами.

План лекції:

§1. Визначений інтеграл із змінною верхньою межею. Теорема про існування первісної функції.

§ 2. Формула Ньютона – Лейбніца.

§3. Заміна змінної у визначеному інтегралі.

§4. Формула інтегрування частинами.

§1. Визначений інтеграл із змінною верхньою межею.

Теорема про існування первісної функції.

Розглянемо одну з основних теорем інтегрального числення, а саме, що всяка неперервна на відрізку [a; b] функція має первісну, та знайдемо спосіб обчислення визначеного інтеграла.

Нехай на відрізку [a; b] задана неперервна функція f(x). Ця функція інтегрована на будь-якому відрізку [a; x], де а≤x≤b. Отже, існує визначений інтеграл який називають визначеним інтегралом із змінною верхньою межею. Очевидно, він є функцією вію х. Позначимо його через

(16)

Оскільки визначений інтеграл не залежить від змінної інтегрування, то щоб не плутати з верхньою межею, ми через f позначили змінну інтегрування.

Л е м а. Якщо функція f(x) неперервна на відрізку [a; b], то функція

також неперервна на цьому відрізку.

Д о в е д е н н я. Нехай х - довільна точка відрізка [a; b]. Надамо х довільного приросту h такого, щоб x+h [a; b]. Знайдемо приріст функції Ф(х) у точці х

Застосуємо до першого інтеграла властивість визначеного інтеграла. Матимемо

До останнього інтеграла застосуємо теорему про середнє:

, (17)

Маємо:

Це означає, що функція Ф(х) є неперервною в точці х. Оскільки х - довільна точка відрізка [a; b], то Ф(х) неперервна в кожній точці цього відрізка. Лему доведено.

Основна теорема інтегрального числення

Т е о р е м а. Якщо функція f(x) є неперервною на відрізку [a; b], то функція є диференційованою в кожній точці цього відрізка і .

Д о в е д е н н я. Нехай х - довільна точка відрізка [a; b], а h наскільки малий приріст х, що x+h [a; b]. Тоді

Оскільки f(x) неперервна на відрізку [a; b], отже, і на відрізку [x; x+h], то до останнього інтеграла можна застосувати формулу (17). Маємо

,

Знайдемо

тобто

Теорему доведено.

Цю теорему читають ще й так:

Якщо f(x)є неперервною на відрізку [a; b], то похідна від визначеного інтеграла із змінною верхньою межею по верхній межі дорівнює підінтегральній функції, в якій змінну інтегрування замінено верхньою межею

Н а с л і д о к. Для будь-якої неперервної на відрізку [a; b] функції f(x) існує первісна, і однією з первісних функцій є визначений інтеграл (16) із змінною верхньою межею.

Справді, оскільки f(x) неперервна на відрізку [a; b], то вона є інтегрованою на [a; b], а отже, і на будь-якому відрізку [a; x], a≤x≤b. Тоді згідно з лемою , функція Ф(х) неперервна на відрізку [a; b], а з доведеної теореми випливає, що Ф(х) має похідну на відрізку [a; b].