§2. Невласні інтеграли другого роду

Невласні інтеграли другого роду – це інтеграли від розривних (необмежених) функцій

Нехай неперервна на проміжку та при х = а має розрив 2-го роду.

Означення. називається невласним інтегралом від розривної (необмеженої) функції .

Якщо ця границя існує, то інтеграл називається збіжним, а якщо не існує, то — розбіжним.

Для обчислення таких невласних інтегралів використовують такі формули:

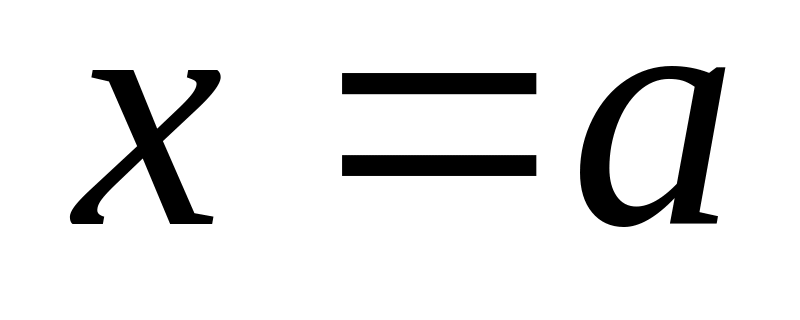0. — точка розриву ,

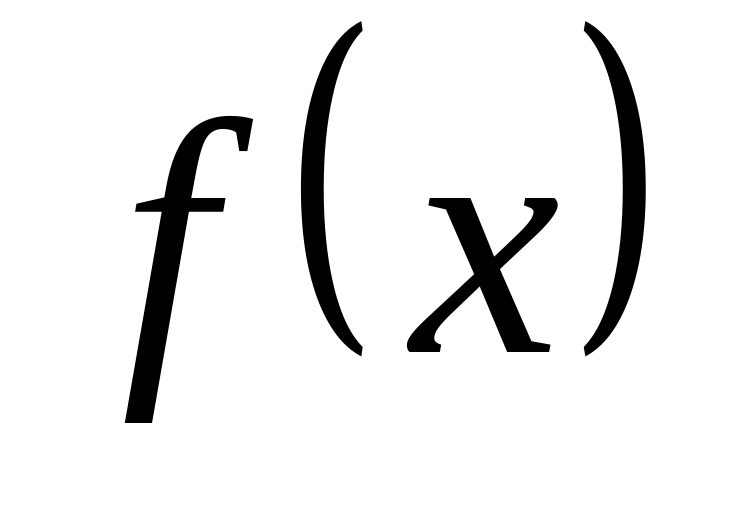. (30.6)

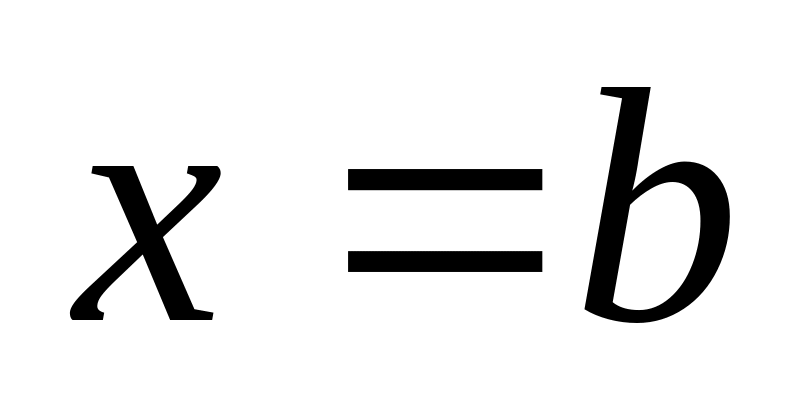0. — точка розриву ,

(30.7)

III. — точка розриву ,

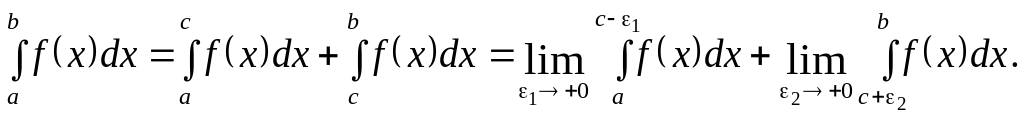(30.8)

Зауваження. До невласних інтегралів, які мають точку розриву, що є внутрішньою для не можна застосувати формулу Ньютона—Лейбніца.

Приклад. Обчислити .

l Неправильне розв’язання: .

Правильне розв’язання: , — точка розриву 2-го роду функції — невласний.

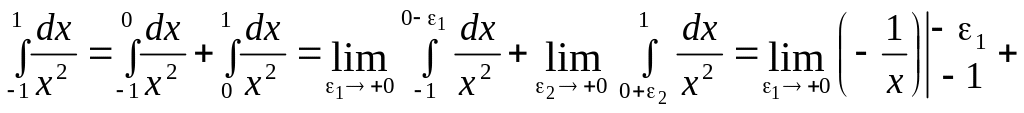
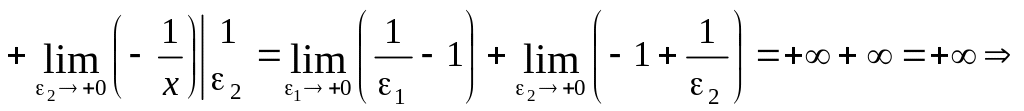інтеграл розбіжний.

§ 3. Інтеграли, що залежать від параметра

Нехай підінтегральна функція визначена в прямокутній області D, так що , ; тоді інтеграл виду

буде функцією допоміжного аргументу або параметра у. Правило диференціювання функції , тобто правило диференціювання інтеграла, що залежить від параметра, встановлюється такою теоремою:

Теорема . Якщо функція неперервна по для будь-якого сталого та частинна похідна неперервна у прямокутній області d, то виконується формула

(30.9)

Більш загальний випадок, коли межі інтегрування також залежать від параметра у:

,

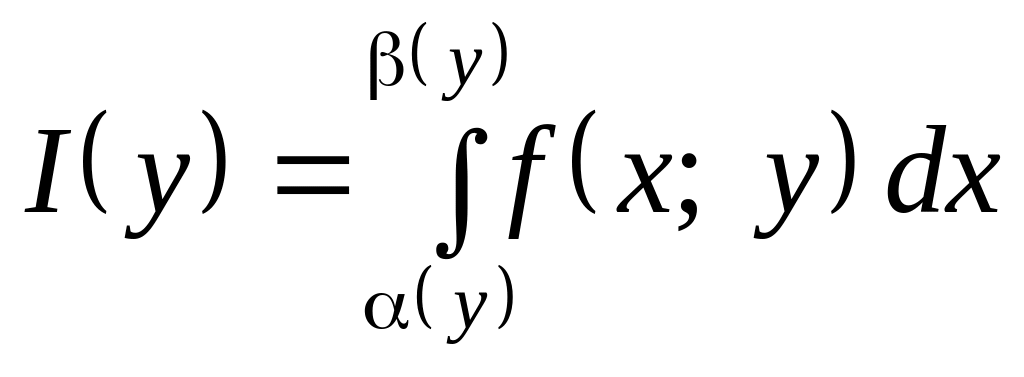визначається такою теоремою:

Теорема . Якщо функція та її частинна похідна неперервні в прямокутній області D, функції та — диференційовні і їхні графіки не виходять за межі області D, то справджується така формула:

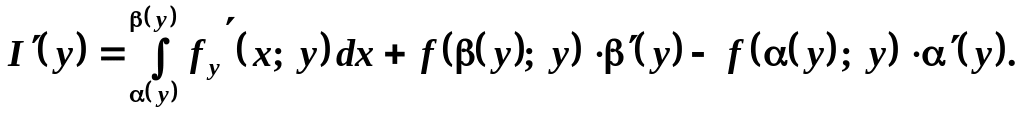
Щоб розпочати застосування формули (7.51) на випадок невласних інтегралів, введемо поняття рівномірної збіжності відносно параметра невласних інтегралів.

І. Нескінченний проміжок інтегрування.

Нехай функція визначена при всіх і всіх , а також існує для кожного невласний інтеграл:

. (7.52)

Означення. Невласний інтеграл (7.52) називається рівномірно збіжним відносно у, якщо для будь-якого знайдеться незалежне від у число , таке що для всіх виконується нерівність

одночасно для всіх .

Розглянемо функцію , що визначена в такій області D:

.

Теорема. Якщо функція та її частинна похідна — неперервні в області D, інтеграл — збіжний, а інтеграл — рівномірно збіжний відносно у, то для виконується формула:

(7.53)

ІІ. Інтеграл від розривної функції.

Нехай функція визначена при всіх і всіх а при має розрив 2-го роду; при цьому існує ін- теграл

. (7.54)

Означення. Невласний інтеграл (7.54) називається рівномірно збіжним відносно у, якщо для будь-якого існує незалежне від у число таке, що при виконується нерівність

одночасно для всіх .

Розглянемо функцію , що визначена в такій області D:

.

Теорема . Якщо функція та її частинна похідна — неперервні в області D, інтеграл — збіжний, а інтеграл — рівномірно збіжний відносно у, то для виконується формула

Ця формула на вигляд така сама, як і формула (30.9), але відрізняється від неї тим, що тут функція при невизначена.

Приклади

1. Обчислити інтеграл .

отже, інтеграл буде збіжним.

2. Обчислити .

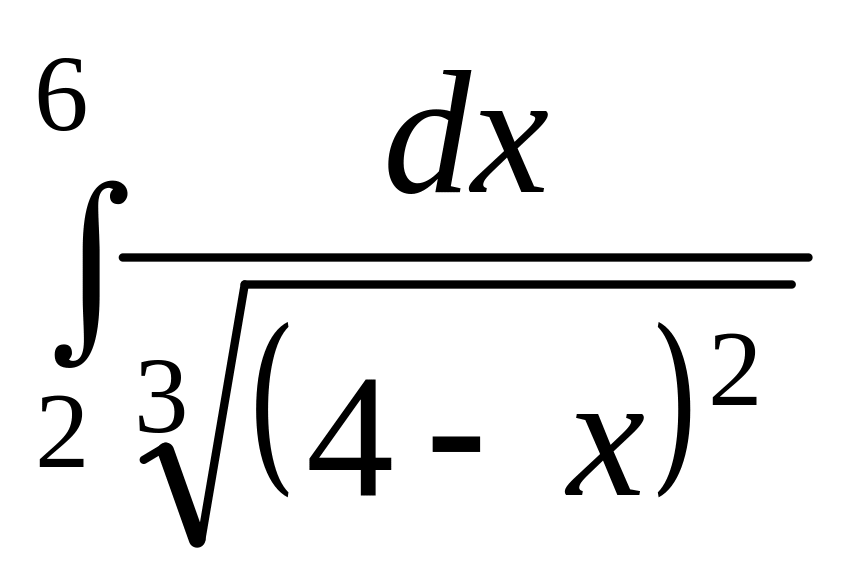Підінтегральна функція має розрив у точці тому

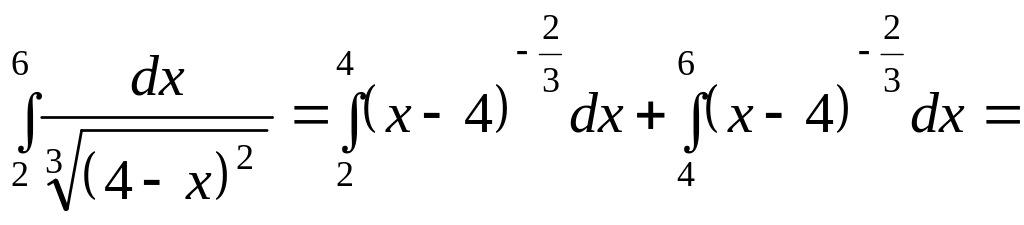
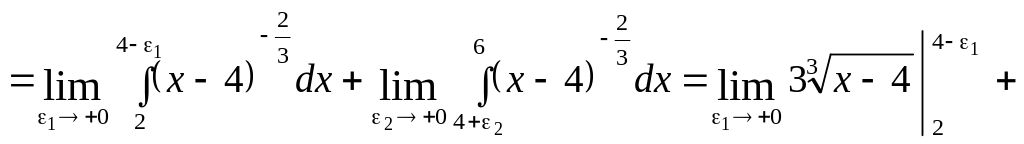
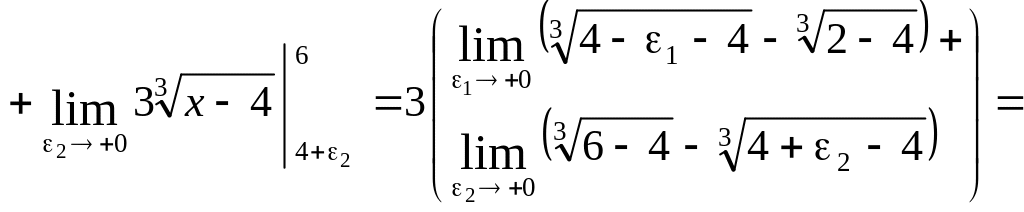
інтеграл збіжний.