
- •Змістовий модуль 5. Інтеграл Рімана. Невласні інтеграли. Лекція № 25
- •Задача про площу криволінійної трапеції.
- •Задача про роботу змінної сили
- •§ 2. Визначеня інтеграла Рімана.
- •Теорема про середнє значення визначеного інтеграла
- •§ 4. Оцінка інтегралів. Формула середнього значення.
- •Лекція № 26
- •Теорема про існування первісної функції.
- •§ 2. Формула Ньютона – Лейбніца.
- •§3. Заміна змінної у визначеному інтегралі
- •§4. Формула інтегрування частинами
- •Лекція № 27
- •§1. Застосування визначеного інтеграла до до обчислення площ плоских областей.
- •§ 2. Означення неперервної кривої. Спрямлювана крива. Застосування визначеного інтеграла до обчислення довжини плоскої кривої.
- •§1. Застосування визначеного інтеграла до до обчислення площ плоских областей.
- •Розв’язання
- •Розв’язання
- •Розв’язання
- •Розв’язання
- •Розв’язання
- •Розв’язання
- •Розв’язання
- •Завдання для самостійної роботи
- •§ 2. Означення неперервної кривої. Спрямлювана крива. Застосування визначеного інтеграла до обчислення довжини плоскої кривої.
- •Обчислення довжини дуги плоскої кривої
- •Зразки розв’язування задач
- •Розв’язання
- •§ 1. Диференціал довжини дуги.
- •§ 2. Кривизна кривої. Коло кривизни. Еволюта. Евольвента.
- •§ 1. Диференціал довжини дуги.
- •§ 2. Кривизна кривої. Коло кривизни. Еволюта. Евольвента.
- •Лекція № 29
- •§ 2. Площа поверхні обертання.
- •§2. Невласні інтеграли другого роду
- •§ 3. Інтеграли, що залежать від параметра
- •Теорема . Якщо функція неперервна по для будь-якого сталого та частинна похідна неперервна у прямокутній області d, то виконується формула
- •Лекція № 31
- •§1. Виконання модульної контрольної роботи № 3.
§ 2. Площа поверхні обертання.
Площа поверхні, утвореної обертанням навколо осі дуги гладкої кривої, заданої функцією , , обчислюється за формулою
![]() .
(29.7)
.
(29.7)
Якщо
гладка крива задана рівнянням
,
![]() ,
то площа поверхні, утвореної обертанням
кривої навколо осі
,
може бути обчислена за формулою
,
то площа поверхні, утвореної обертанням
кривої навколо осі
,
може бути обчислена за формулою
![]() .
(29.8)
.
(29.8)
У
разі параметричного
задання кривої
рівняннями
![]() ,
,
![]() ,
,
![]() ,
де функції
,
де функції
![]() ,
,
![]() - неперервні разом із своїми похідними,
відповідні площі поверхні обчислюються
за формулами:
- неперервні разом із своїми похідними,
відповідні площі поверхні обчислюються
за формулами:
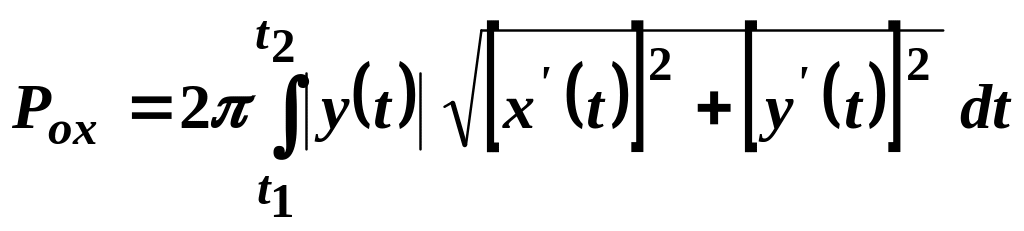 ,
(29.9)
,
(29.9)
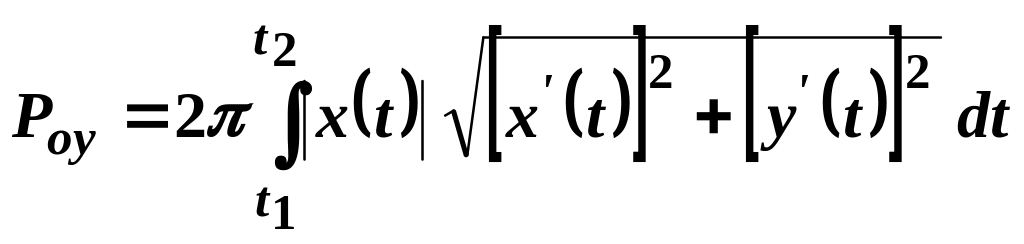 .
(29.10)
.
(29.10)
Площа
поверхні, отриманої обертанням навколо
полярної
осі криволінійного
сектора, обмеженого неперервною кривою
та двома полярними радіусами
![]() ,
,
![]() ,
визначається за формулою
,
визначається за формулою
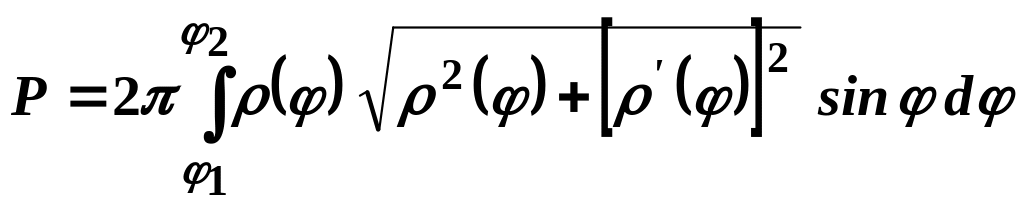 .
(29.11)
.
(29.11)
Зразки розв’язування задач
1. Знайти площу поверхні сфери, як тіла обертання.
Розв’язання
Нехай
сфера утворена обертанням кола
навколо осі
.
Знайдемо
![]() :
:
(верхня
половина кола), тоді
![]()
![]() .
.
Обчислимо
![]() ,
тоді
,
тоді
![]() .
.
Отже, за формулою (3.17):
![]() .
.
Площа
поверхні сфери дорівнює
![]() .
.
2.
Знайти бічну поверхню параболоїда,
утвореного обертанням параболи
![]() навколо осі
на відрізку
навколо осі
на відрізку
![]() .
.
Розв’язання
Якщо
,
то
![]() .
.
Т ак
як вітки параболи симетричні відносно
осі
,
будемо вважати, що тіло утворено
обертанням верхньої вітки, рівняння
якої
ак
як вітки параболи симетричні відносно
осі
,
будемо вважати, що тіло утворено
обертанням верхньої вітки, рівняння
якої
![]() .
Отже,
.
Отже,
![]() .
Тоді
.
Тоді
![]() .
.
Тепер
![]()
![]() .
.
Маємо:
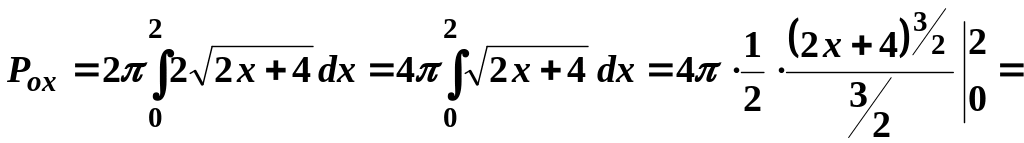
![]()
![]() кв.
од.
кв.
од.
3.
Знайти площу поверхні, утвореної
обертанням навколо осі
дуги синусоїди
![]() від
до
від
до
![]() .
.
Розв’язання
Скористуємось
формулою (29.10).
Спочатку
знайдемо
![]()
![]() ,
тоді
,
тоді
![]() .
.
Отже,
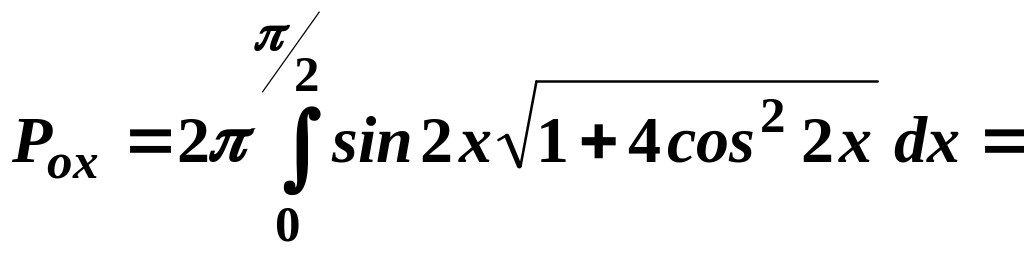
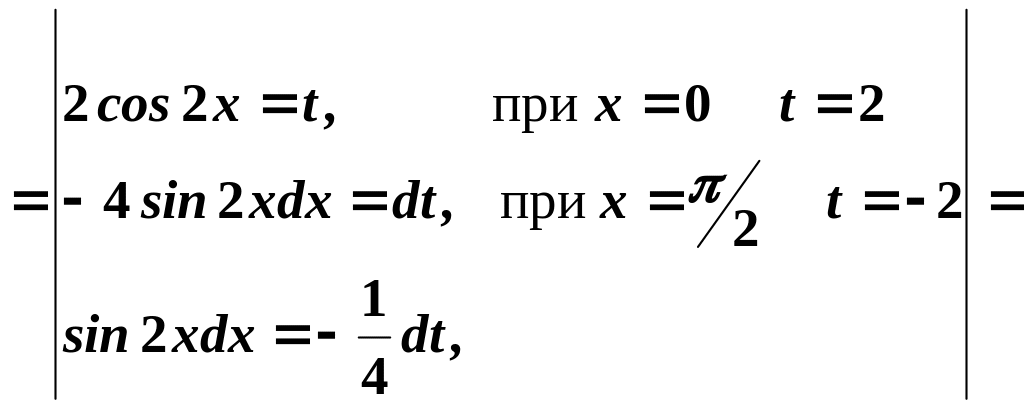
![]() .
.
Позначимо
![]() та обчислимо його частинами. Будемо
мати:
та обчислимо його частинами. Будемо
мати:
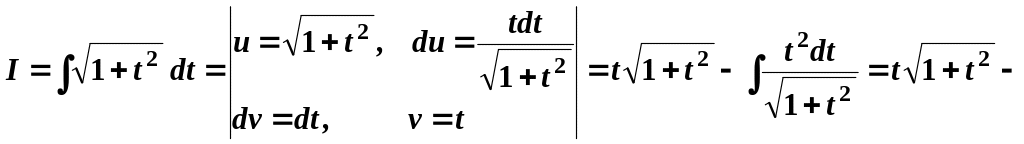
![]() .
.
Звідки
![]() ,
тому
,
тому
![]() .
.
Повернемося до обчислення площі поверхні:
![]()
![]()
![]() кв.
од.
кв.
од.
4.
Знайти площу поверхні, отриманої
обертанням прямої
![]() навколо осі
навколо осі
![]() від
до
від
до
![]() .
.
Розв’язання
Виразимо
:
![]() .
Скористаємось формулою (29.5), для цього
знайдемо
.
Скористаємось формулою (29.5), для цього
знайдемо
![]() ,
тоді
,
тоді
![]() .
.
 Отримаємо:
Отримаємо:
![]()
![]()
![]() кв. од.
кв. од.
5.
Обчислити поверхню тора, утвореного
обертанням кола
![]() навколо осі
.
навколо осі
.
Розв’язання
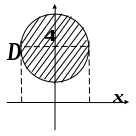
Поверхня
тора дорівнює сумі поверхонь, утворених
обертанням дуг
![]() та
та
![]() навколо осі
.
Щоб скористатися формулою (3.17), розв’яжемо
рівняння кола відносно
.
Маємо:
навколо осі
.
Щоб скористатися формулою (3.17), розв’яжемо
рівняння кола відносно
.
Маємо:![]() ,
звідки
,
звідки
![]() ,
,
![]() .
.
Для
дуги
:
![]() ,
,
![]() ,
,
![]() .
.
Обчислимо
![]() ,
,
![]() .
Для дуги
:
.
Для дуги
:
![]() ,
,
![]() ,
.
,
.
Отже,
![]()
![]() .
.
Відрізок інтегрування симетричний, тобто
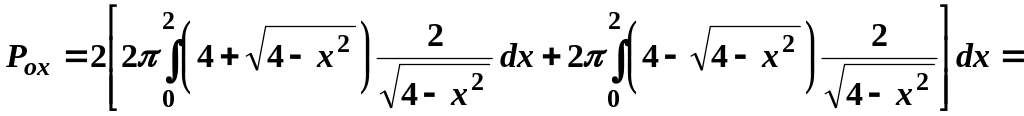
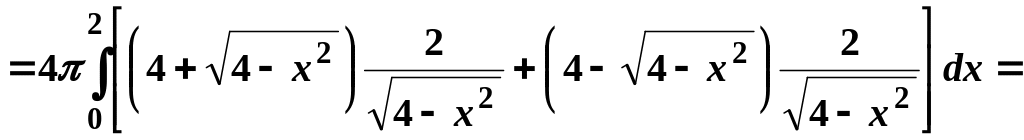
![]()
![]() кв.
од.
кв.
од.
6.
Знайти площу поверхні, утвореної
обертанням навколо осі
кривої
![]()
Розв’язання
Застосуємо
формулу (3.19), для цього знайдемо
![]() ,
,
![]() .
Обчислимо
.
Обчислимо
![]()
![]() .
.
Тоді отримаємо:
![]()
![]() кв.
од.
кв.
од.
7.
Знайти поверхню тіла, утвореного
обертанням однієї арки циклоїди
![]() навколо осі
.
навколо осі
.
Розв’язання
Використовуючи
формулу (29.9), обчислимо спочатку
![]() ,
,
![]() .
.
Тоді
![]()
![]() .
.
Отже,
![]()
![]()
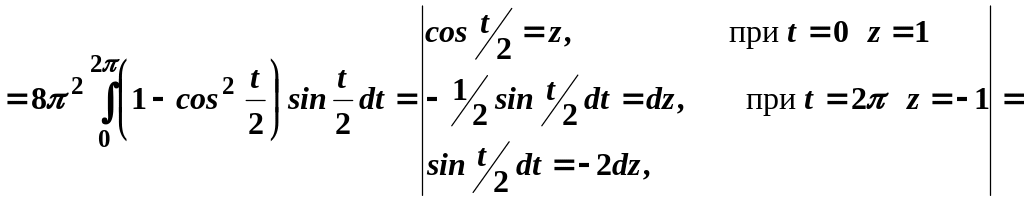
![]()
![]() кв.
од.
кв.
од.
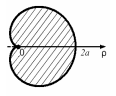
8. Знайти площу поверхні, утвореної обертанням кардіоїди навколо полярної осі.
Розв’язання
Використаємо формулу (29.11), для цього знайдемо:
 EMBED
Equation.3
EMBED
Equation.3
![]() ,
,
![]()
![]()
![]() .
.
![]()
![]()
![]()
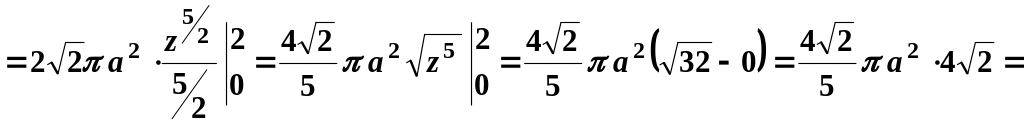
![]() кв.од.
кв.од.
9.
Обчислити площу поверхні тіла, утвореного
обертанням лемніскати
![]() навколо полярної осі.
навколо полярної осі.
Розв’язання
О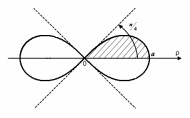 бчислимо
половину шуканої площі поверхні, а саме:
бчислимо
половину шуканої площі поверхні, а саме:
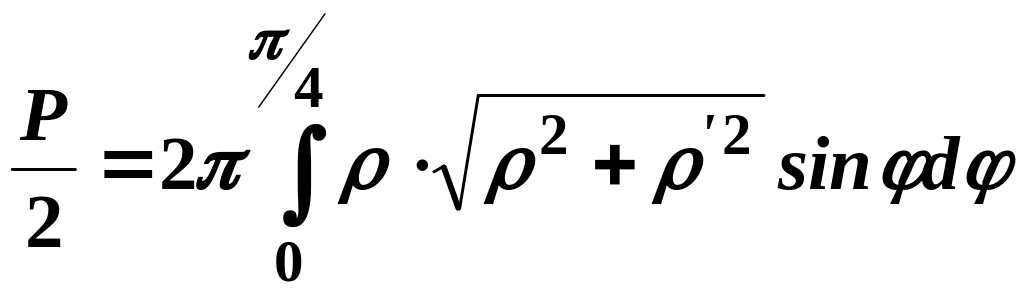 .
Знайдемо з рівняння
.
Знайдемо з рівняння
![]() .
.
Тоді
![]()
![]() .
.
Обчислимо![]()
![]() .
.
Тоді
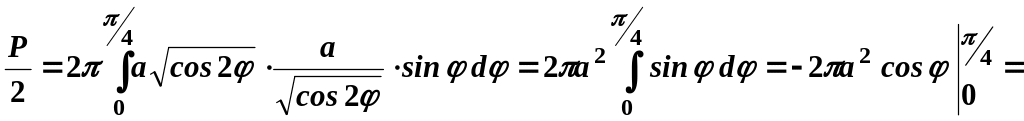
![]() .
.
![]() кв.
од.
кв.
од.
Завдання для самостійної роботи
Обчислити площі поверхонь тіл, утворених обертанням кривих навколо відповідної осі:
1.
![]() ,
,
![]() ,
,
![]() ?
?
2.
,
![]()
![]() ,
?
,
?
3.
![]() ,
,
![]() ,
,
![]() ?
?
4.
![]() ,
,
![]() ,
?
,
?
5. Знайти поверхню сфери, заданої в полярних координатах.
§ 3. (С. р. Знаходження статичних моментів і координат центра мас. Теореми Гульдіна. Обчислення роботи та сили тиску.)
Лекція № 30
Тема: Невласні інтеграли першого роду. Невласні інтеграли другого роду.
План лекції:
§1. Невласні інтеграли першого роду.
§2. Невласні інтеграли другого роду
§1. Невласні інтеграли першого роду.
1. Невласні інтеграли першого роду – це інтеграли із нескінченним проміжком інтегрування.
Нехай
f(x)
інтегровна для будь-якого скінченного
![]() ,
так що
,
так що
![]() існує.
існує.
Означення.
Границя
при
![]() називається невласним
інтегралом від функції f(x)
на нескінченному проміжку
називається невласним
інтегралом від функції f(x)
на нескінченному проміжку
![]() і позначається так:
і позначається так:
![]() .
.
Якщо ця границя існує та скінченна, то невласний інтеграл називається збіжним, а якщо не існує (зокрема нескінченна), то — розбіжним.
Якщо
f(x)
— інтегровна для скінченних a
та b,
тобто
![]() формули для обчислення невласних
інтегралів на нескінченному проміжку
мають вигляд:
формули для обчислення невласних
інтегралів на нескінченному проміжку
мають вигляд:
![]() (30.1)
(30.1)
![]() (30.2)
(30.2)
![]() (30.3)
(30.3)
де
![]()
Приклад. Дослідити на збіжність інтеграл Діріхле
![]() . (30.4)
. (30.4)
Для розв’язування задачі розглянемо такі три випадки:
р = 1.
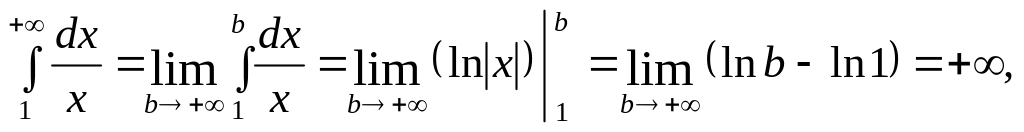 інтеграл розбіжний.
інтеграл розбіжний.
p < 1.
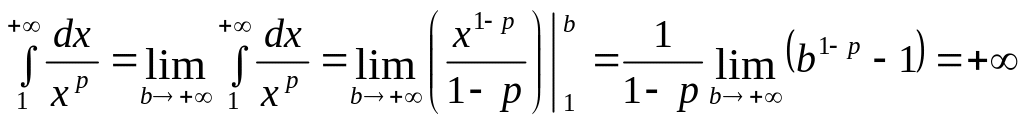 ,
інтеграл розбіжний.
,
інтеграл розбіжний.p > 1.
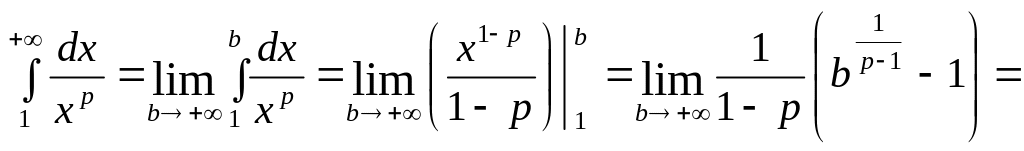
![]() ,
інтеграл збіжний.
,
інтеграл збіжний.
Отже,
інтеграл Діріхле збіжний при p > 1
та розбіжний при
![]() .
.
Крім безпосереднього обчислення невласних інтегралів при дослідженні їх на збіжність існують і інші методи.
Одним із таких методів можна встановити збіжність інтеграла Пуассона (рис. 30.1)
Рис. 30.1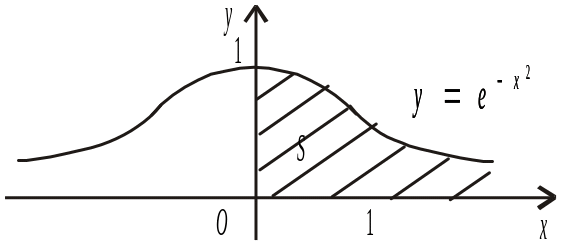
![]() , (30.5)
, (30.5)
особливість
якого полягає в тому, що
первісна для підінтегральної функції
![]() не виражається через елементарні
функції.
не виражається через елементарні
функції.
У деяких випадках достатньо встановити лише збіжність чи розбіжність розглядуваного інтеграла, при цьому можна скористатися методом порівняння, що базується на такій теоремі:
Теорема
1. Якщо
при
![]() виконується нерівність
виконується нерівність
![]() ,
то зі збіжності інтеграла
,
то зі збіжності інтеграла
![]() випливає збіжність інтеграла
випливає збіжність інтеграла
![]() або з розбіжності
випливає розбіжність
.
або з розбіжності
випливає розбіжність
.
Звичайно, для порівняння вибирається інтеграл, збіжність якого відома, наприклад інтеграл Діріхле.
Приклад.
Дослідити збіжність інтеграла
![]() .
.
l ![]() .
.
![]() — збіжний,
як інтеграл Діріхле із р
= 2 > 1, тому буде збіжним і
— збіжний,
як інтеграл Діріхле із р
= 2 > 1, тому буде збіжним і
![]() .
.
