Лекція № 29

Тема: Об’єм тіла обертання. Площа поверхні обертання. (С. р. Знаходже ння статичних моментів і координат центра мас. Теореми Гульдіна. Обчислення роботи та сили тиску.)

План лекції:

t

§ 1. Об’єм тіла обертання.

§ 2. Площа поверхні обертання.

§ 3. (С. р. Знаходження статичних моментів і координат центра мас. Теореми Гульдіна. Обчислення роботи та сили тиску.)

§ 1. Об’єм тіла обертання.

Нехай функція - неперервна і додатна на відрізку .

Об’єм тіла, яке утворюється при обертанні навколо осі криволінійної

трапеції, обмеженої кривою та відрізками прямих (рис.3.6), дорівнює

. (29.1)

Якщо задані дві неперервні криві такі, що , при , то об’єм тіла, отриманого обертанням навколо осі плоскої фігури, обмеженої цими лініями та відрізками прямих (рис.3.7), обчислюється за формулою

. (29.2)

Рис. 3.7

Рис. 3.6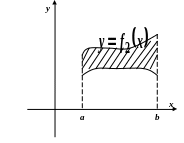

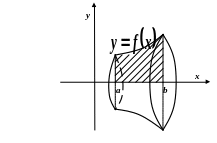
Рис. 3.6

О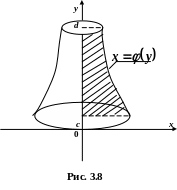 б’єм тіла, утвореного обертанням навколо осі криволінійної трапеції, обмеженої неперервною кривою , прямою та відрізками прямих , (рис.3.8), дорівнює

. (29.3)

У разі параметричного задання кривої рівняннями , , об’єми утворених тіл обертання навколо осі або осі визначаються відповідно формулами:

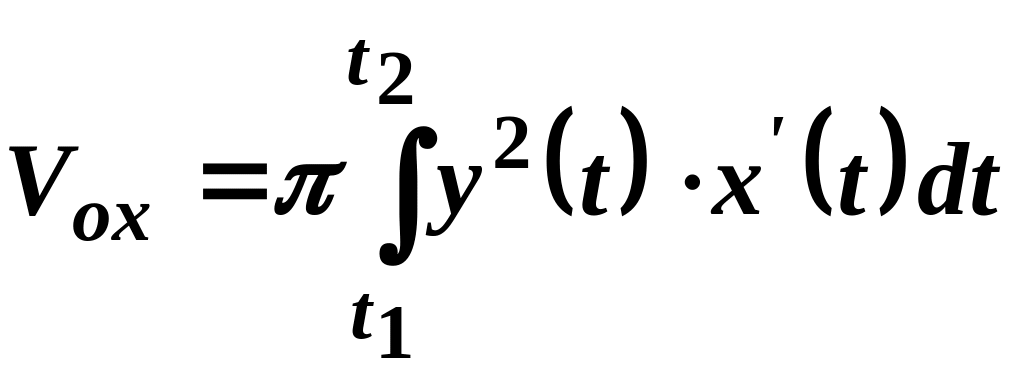, (29.4)

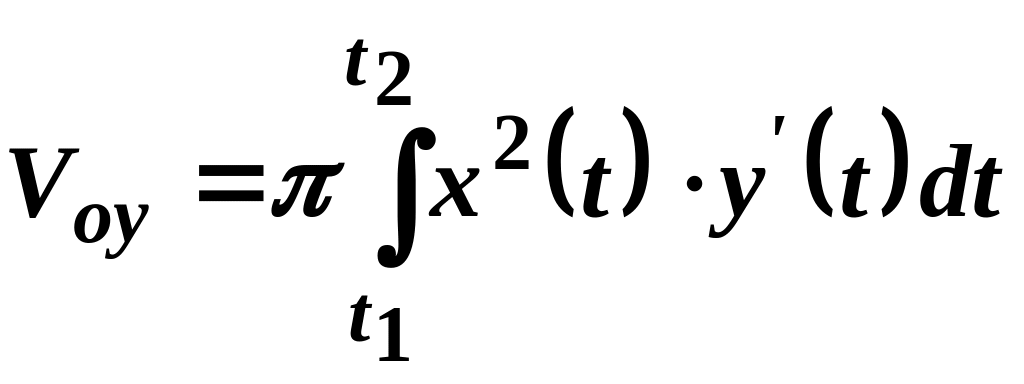. (29.5)

Н

Рис. 3.9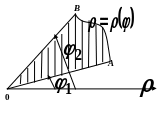

ехай крива задана в полярній системі координат рівнянням , де - неперервна функція при . Тоді об’єм тіла, утвореного обертанням навколо полярної осі плоскої фігури, обмеженої кривою та двома полярними радіусами і , які відповідають кутам та (рис.3.9), обчислюється за формулою

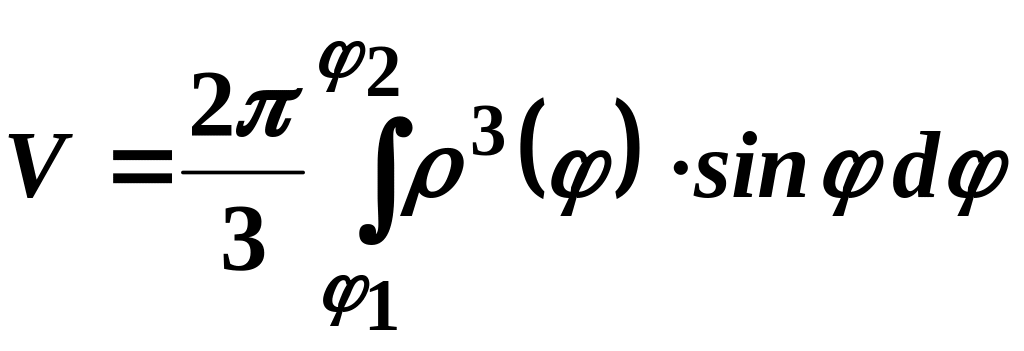. (29.6)

Зразки розв’язування задач

1. Знайти об’єм кулі.

Розв’язання

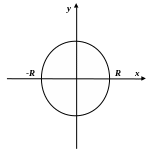
Нехай куля утворена обертанням навколо осі кола . Звідки .

Для обчислення використаємо формулу (3.11), враховуючи, що .

Отже,

куб. од.

2. Обчислити об’єм тіла, утвореного обертанням навколо осі фігури, обмеженої лініями , , , .

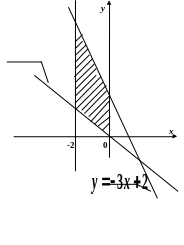
Розв’язання

Скористаємось формулою (29.4):

= куб. од.

3. Знайти об’єм тіла, утвореного обертанням навколо осі фігури, обмеженої лініями та .

Розв’язання

Рівняння задає параболу з вершиною в точці , віссю симетрії якої є вісь .

Щоб знайти межі інтегрування, шукаємо ординати точок перетину ліній: , тоді , звідки , .

Зважаючи на симетрію тіла відносно осі , за формулою (3.13) маємо:

куб. од.

В завданнях 4 – 7 обчислити об’єми тіл, утворених обертанням навколо осі фігури, обмеженої заданими лініями.

4. , , .

Розв’язання

Знайдемо межі інтегрування: , тоді , тоді , звідки . При маємо .

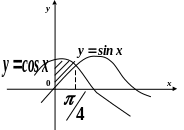
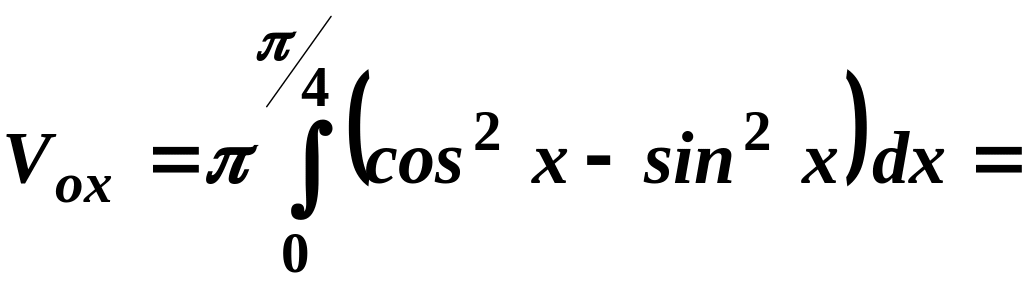
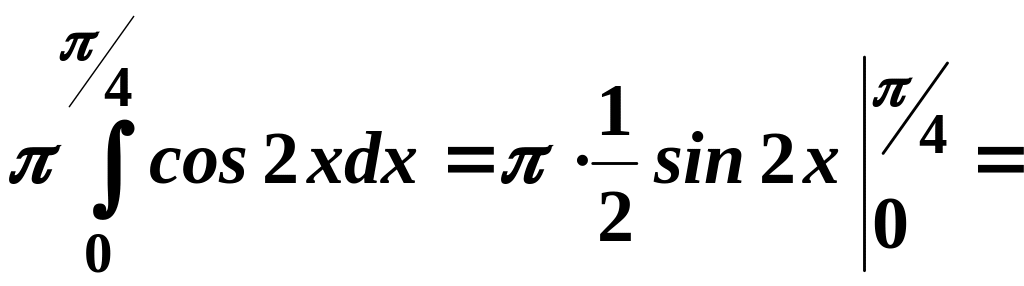
куб. од.

5. , , .

Розв’язання

З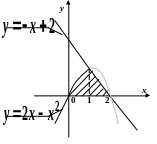 образимо фігуру, при обертанні якої утворюється шукане тіло.

Знайдемо точки перетину графіків функцій та . , звідки , . Знайдемо .

Наша парабола перетинає вісь в точках та .

Так як на відрізках та фігура обмежена різними лініями, то об’єм тіла знайдемо як суму об’ємів , де

,

.

Тоді куб. од.

6. , , .

Розв’язання

Побудуємо вітку параболи та пряму . Вони перетинаються в точці:

, .

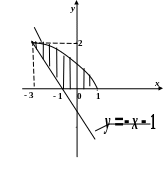
Пряма перетинає вісь в точці .

Вітка параболи з віссю має спільну точку .

Знайдемо об’єм тіла як різницю між об’ємами - об’ємом тіла, утвореного обертанням гілки параболи, та - об’ємом конуса, утвореного обертанням прямої.

Маємо:

куб. од.

7.

Розв’язання

Для обчислення об’єму скористаємось формулою (29.4). Знайдемо . Тоді

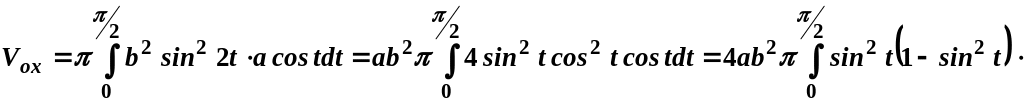
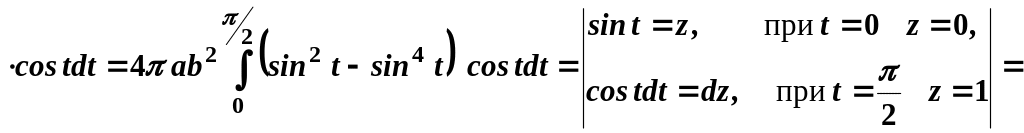
куб. од.

8. Знайти об’єм тіла, утвореного обертанням однієї арки циклоїди .

Розв’язання

Знайдемо , .

Тоді

.

Обчислимо останній інтеграл:

.

Отже,

куб. од.

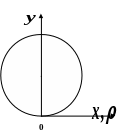
9. Обчислити об’єм тіла, отриманого обертанням кривої навколо полярної осі.

Розв’язання

Рівняння задає коло діаметра з центром у точці . Зрозуміло, що . Для обчислення об’єму використаємо формулу (29.6). Будемо мати:

куб. од.

Завдання для самостійної роботи

Обчислити об’єми тіл, утворених обертанням плоских фігур навколо координатних осей:

1. , , , , ?

2. , , ?

3. , , ?

4. , , ?

5.

6. Знайти об’єм тіла, утвореного обертанням кривої навколо полярної осі .

Обчислити об’єм тіла, утвореного обертанням фігури, що обмежена лініями:

16. навколо осі Оу.

Відповідь. .

17. навколо осі Оу.

Відповідь. .

18. навколо осі Ох.

Відповідь. .

19. навколо осі Ох.

Відповідь. .

20. ху = 4, х = 1, х = 4, у = 0 навколо осі Ох.

Відповідь. .