Змістовий модуль 5. Інтеграл Рімана. Невласні інтеграли. Лекція № 25

Тема: Задачі, що приводять до поняття визначеного інтеграла. Означення інтеграла Рімана. Властивості сум Дарбу. Критерій інтегровності функції. Класи інтегровних функцій.

План лекції:

§ 1 Задачі, що приводять до поняття визначеного інтеграла.

§ 2 Означення інтеграла Рімана.

§ 3 Властивості сум Дарбу. Критерій інтегровності функції.

§ 4 Класи інтегровних функцій.

§1. Задачі, що приводять до поняття визначеного інтеграла.

1. Задача про площу криволінійної трапеції.

Нехай в площині XOY дано фігуру ABCD, обмежену відрізком [а;b] осі OX, прямими х=а, х=b і кривою y=f(x), де f(x) – неперервна , невід’ємна на відрізку [а;b] функція.

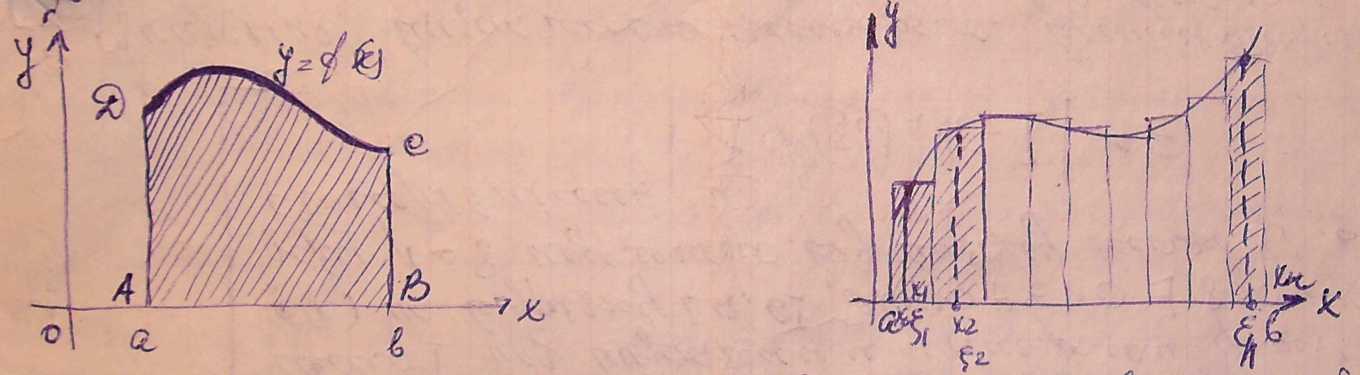
Така фігура називається криволінійною трапецією з основою [а;b].

Поставимо задачу: знайти площу криволінійної трапеції. Розіб’ємо відрізок [а;b] на n частин точками х₀=а, х₁, …, х_n-1, х_n=b (х₀< х₁<…<х_n) і через точки поділу проведемо вертикальні прямі.

Тоді прямолінійна трапеція розіб’ється на n трапеції з основами [х₀; х₁], …, [х_n-1; х_n]. На кожній з основ візьмемо довільну точку ( ) і побудуємо прямокутники з основою [х_і-1; х_і] і висотою (і=1,…,n). Площа кожного прямокутника дорівнює ( х_і;х_і-1).

Розглянемо східчасту фігуру, складену з прямокутників з основами

[х₀; х₁], …, [х_n-1; х_n]; її площу, що дорівнює сумі

,

будемо вважати наближено рівною площі S криволінійної трапеції ABCD

За площу криволінійної трапеції природно взяти границю, до якої прямує площа побудованих таким чином ступінчастих фігур при необмеженому збільшенні числа відрізків і прямування до нуля довжин відрізків ділення.

Таким чином або

2. Задача про роботу змінної сили

Матеріальна точка переміщується під дією сили , що направлена вздовж осі ОХ з точки х=а в точку b (a<b). Припускаємо, що функція не перервна на відрізку [а;b].

Так, як і в попередньому пункті, розбиваємо відрізок [а;b] на n частин і в кожній з них візьмемо довільну точку .

Вважаючи силу F сталою на відрізку [х_і-1; х_і], одержимо наближене значення роботи А.

Точне значення роботи одержуємо при наближеному збільшенні числа відрізків і прямуванні до нуля довжин відрізків ділення.

§ 2. Визначеня інтеграла Рімана.

Будимо розглядати суми і границі з попереднього пункту, абстрагуючись від їх конкретного змісту.

Нехай на відрізку [а;b] осі ОХ задана довільна функція . Розіб’ємо відрізок на n частин точками х₀=а, х₁, …, х_n-1, х_n=b (х₀< х₁<…<х_n). На кожному з відрізків [х_і-1; х_і] (і=1,…,n) в середині або на кінцях візьмемо по точці. Позначимо ці точки відповідно . Складемо суму

,

або коротше (1)

Ця сума називається інтегральною сумою для функції на відрізку [а;b].

Вона не залежить від способу розбивання відрізка [а;b] на частини

[х₁; х₀], …, [х_n; х_n-1] і від вибору точок .

Для функції можна скласти незлічену множину інтегральних сум. Позначимо через довжину найбільшого часткового відхилення розбиття: .

Означення: Якщо існує спільна границя інтегральної суми при , то ця границя називається визначеним інтегралом від функції , на відрізку [а;b] і позначається таким чином

(2) або

У цьому випадку функція називається інтегрованою на [а;b] числа a і b називаються відповідно нижньою і верхньою межею інтегрування, підінтегральною функцією, х- змінною інтегрування.

Означення визначеного інтеграла на «мові ε – δ »:

Число І називається визначеним інтегралом функції на відрізку [а;b], якщо така, що при незалежно від вибору точок виконується нерівність

З означення визначеного інтеграла випливає, що величина інтеграла (2) залежить тільки від виду функції і від чисел a і b. Отже, якщо задані і межі інтегрування, то інтеграл (2) визначається однозначно являє собою деяке число.

Т. (Достатня умова інтегрованості функції)

Якщо функція неперервна на відрізку [а;b] то вона інтегрована на ньому, тобто так, при виконується нерівність

Доведено, що визначений інтеграл існує не тільки для неперервних функцій. Клас інтегральних функцій більш широкий. Наприклад, множна довести, що існує інтеграл від функцій які обмежені і мають скінченне число точок розриву.

Повертаючись до задачі 1 бачимо, що:

1. Площа S криволінійної трапеції, обмеженої відрізком [а;b] осі абцис, прямими х=а, х=b і кривою y=f(x), де f(x) – неперервна , невід’ємна на відрізку [а;b] функція, чисельно дорівнює визначеному інтегралу від функції на відрізку [а;b]:

2. Робота направленої вздовж осі ОХ змінної сили по переміщенню одиниці маси вздовж осі ОХ із точки х=а в точку х=b чисельно дорівнює визначеному інтегралу від функції на відрізку [а;b]

Перша задача дозволяє визначити геометричний зміст визначеного інтаграла, а саме

визначений інтеграл від невід’ємної функції на відрізку [а;b] чисельно дорівнює площі криволінійної трапеції з основою [а;b], обмеженої зверху кривою y=