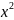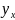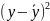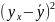- •Соян ш.Ч. Статистика
- •Содержание
- •Глава 1. Общие основы теории статистики……………………...5
- •Глава 2. Статистическое наблюдение……………………………..16
- •Глава 3. Сводка и группировка статистических материалов……………………………………………………………………29
- •Глава 1. Общие основы теории статистики
- •Понятие статистики.
- •Понятие статистики
- •Предмет статистики. Основные категории статистики
- •Структура статистической науки
- •1.4. Статистическая методология
- •1.5. Организация государственной статистики в
- •2.2. Организационные формы, виды и способы статистического наблюдения
- •2.3. Программно-методологические вопросы статистического наблюдения
- •2.4. Ошибки наблюдения
- •3.2. Виды группировок
- •3.3. Методологические вопросы проведения группировок. Особенности их решения для разных видов группировок
- •3.4. Практическое решение задач проведения группировок
- •Предварительная группировка фермерских хозяйств по размеру
- •Группировка фермерских хозяйств по размеру
- •Распределение числа малых предприятий Республики Тыва по отраслям экономики
- •Основные показатели деятельности промышленных предприятий
- •Предварительная группировка предприятий по объему производимой продукции
- •Аналитическая группировка предприятий
- •3.5. Ряды распределения
- •Распределение сотрудников фирмы по уровню образования
- •3.6. Система группировок
- •Глава 4.Статистические величины
- •Относительная величина планового задания:
- •Относительная величина выполнения плана:
- •Объем платных услуг населению Республики Тыва по видам
- •4.2. Понятие средней величины. Виды средних величин
- •Виды степенных средних величин
- •4.3. Правила выбора формы средних
- •Затраты на производство продукции
- •Группировка предприятий по уровню заработной платы
- •Характеристика выпускаемой продукции
- •4.4. Средняя арифметическая. Способы расчета средней арифметической
- •Группировка трехкомнатных квартир по стоимости
- •4.5. Структурные средние
- •Ряд распределения по среднедушевому доходу населения
- •Показатели вариации
- •Распределение семей по уровню среднедушевого дохода
- •5.3. Правило сложения дисперсии
- •Распределение магазинов по объему товарооборота
- •6.2. Ряды динамики, их классификация
- •6.3. Правила построения рядов динамики
- •6.4. Показатели анализа рядов динамики
- •Расчет показателей динамики
- •Численность трудовых ресурсов за ряд лет
- •Динамика выпуска продукции
- •6.5. Способы выравнивания динамических рядов. Экстраполяция и интерполяция
- •Производство продукции по месяцам
- •Производство продукции по кварталам
- •Сглаживание ряда динамики методом аналитического выравнивания
- •Производство продукции по месяцам
- •7.2. Агрегатная форма индексов
- •Данные для расчета индивидуальных и агрегатных индексов
- •Динамика реализации продукции в отчетном периоде по сравнению с базисным
- •Динамика затрат на производство продукции
- •7.3. Индексы средних величин
- •Динамика затрат на производство продукции
- •7.4. Территориальные индексы
- •Сравнительная характеристика товарооборота Новосибирской и Томской областей
- •8.2. Задачи изучения взаимосвязей
- •8.3. Понятие корреляционно-регрессионного анализа, условия его применения
- •Расчет параметров
- •8.4. Показатели тесноты связи, линейный коэффициент корреляции
- •8.5. Меры оценки тесноты связи для атрибутивных признаков
- •Данные для расчета коэффициентов Фехнера, Спирмена и Кендалла
- •Шкала оценки тесноты связи
- •Макет таблицы сопряженности 2х2
- •Зависимость уровня образования от пола
- •9.2. Способы формирования выборочной совокупности
- •9.3. Средняя и предельная ошибки выборки
- •Формулы определения средней ошибки для различных способов отбора
- •9.4. Использование результатов выборочного наблюдения
- •Глоссарий
- •Библиографический список
8.3. Понятие корреляционно-регрессионного анализа, условия его применения
Корреляционно-регрессионный анализ (КРА) – один из методов многомерного статистического анализа, в котором форма и интенсивность связи представлены в формализированном виде, т.е. в виде математических уравнений и формул.
КРА можно применять при соблюдении следующих условий:
Должна быть достаточная численность наблюдений (как правило, считается, что число факторов должно быть меньше числа наблюдений в 6-8 раз);
Наблюдения должны быть статистически независимы;
Совокупность, по которой рассчитывается КРА, должна быть однородна (подчиняться одному закону развития);
Должны быть количественные переменные.
Выполнение условий 1-4 необходимо для того, чтобы применять результаты КРА для прогнозных, нормативных, перспективных расчетов. Иначе результаты КРА пригодятся только для объяснения фактов [1].
Выделяют две основные задачи КРА:
- оценка параметров уравнения регрессии, т.е. уравнения, которое описывает взаимосвязь между факторами х и у (задача регрессионного анализа);
- оценка тесноты связи (задача корреляционного анализа).
Для оценки параметров используется несколько методов математической статистики:
- наименьших квадратов;
- наименьших расстояний;
- избранных точек.
Рассмотрим технологию оценки параметров методом наименьших квадратов на простейшем примере: один фактор, один результат, связь прямая.
Метод наименьших квадратов.
Идея метода: теоретическая прямая строится таким образом, чтобы был минимум Δ:
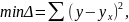
где
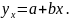
Решая относительно а и в это уравнение, находим оценки параметров:
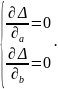
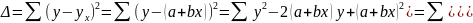
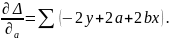
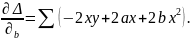


Решая систему линейных нормальных уравнений относительно а и в, получим оценки параметров а и в, обеспечивающие minΔ.
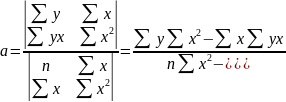
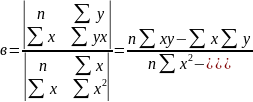
Пример оценки параметров уравнения регрессии.
Имеются данные о стаже и выработке (графы 1-2, табл. 33):
Таблица 33
Расчет параметров
№ п.п. |
Стаж х |
Месячная выработка у |
|
xy |
|
|
|
|
A |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
11 |
4,0 |
220 |
16,0 |
880,0 |
48400 |
266,06 |
5712,3364 |
871,43 |
22 |
6,5 |
310 |
42,25 |
2015,0 |
96100 |
282,90 |
207,9364 |
160,846 |
33 |
4,2 |
327 |
17,64 |
1373,4 |
106929 |
267,41 |
987,2164 |
793,718 |
44 |
4,5 |
275 |
20,25 |
1237,5 |
75625 |
269,43 |
423,5364 |
683,953 |
55 |
6,0 |
280 |
36,0 |
1680,0 |
78400 |
279,53 |
242,7364 |
257,602 |
66 |
4,5 |
253 |
20,25 |
1138,5 |
64009 |
269,43 |
1813,0564 |
683,953 |
77 |
4,7 |
245 |
22,09 |
1151,5 |
60025 |
270,77 |
2558,3364 |
615,313 |
88 |
16,0 |
340 |
256,0 |
5440,0 |
115600 |
346,88 |
1973,1364 |
2631,69 |
99 |
13,2 |
312 |
174,24 |
4118,4 |
97344 |
328,02 |
269,6164 |
1052,48 |
10 |
14,0 |
352 |
196,0 |
4928,0 |
123904 |
333,41 |
3183,2164 |
1431,11 |
11 |
11,0 |
325 |
121,0 |
3575,0 |
105625 |
313,21 |
865,5364 |
310,641 |
12 |
12,0 |
308 |
144,0 |
3696,0 |
94864 |
319,94 |
154,2564 |
593,41 |
Итого |
100,6 |
3547 |
1065,72 |
31233,3 |
1066825 |
- |
18390,917 |
10086,1 |
Построим уравнение связи между стажем и месячной выработкой.
Определим параметры уравнения регрессии по приведенным выше формулам (промежуточные расчеты оформим в табл. 32 (графы 3-5).
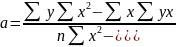

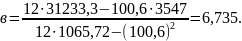
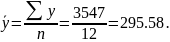
Таким образом, получилось уравнение регрессии:
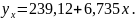
На основании полученного уравнения рассчитаем теоретические уровни признака у (по уравнению связи, подставляя в него значения признака х). Результаты расчетов занесем в табл. 32.
Интерпретация полученных параметров:
Чаще всего параметр а не имеет экономической интерпретации. Иногдаа показывает начальный уровень у, т.е. значение у при х = 0.
Параметр в – сила связи, т.е. увеличение стажа на 1 год в среднем приводит к увеличению выработки на 6,735 руб.