Динамика затрат на производство продукции

Предприятие	Себестоимость единицы продукции, у.е.		Количество продукции, шт.
	Базисный период	Отчетный период		Базисный период	Отчетный период
1	256	320		1480	1500
2	250	315		2000	2200
Итого	-	-		3480	3700

Определим, как изменилась средняя себестоимость на производство единицы продукции по отрасли всего и в том числе за счет отдельных факторов.

Средние затраты рассчитаем при помощи средней арифметической взвешенной, затем найдем индекс переменного состава:

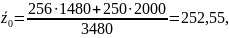
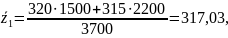
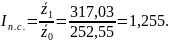
Таким образом, средняя себестоимость в целом по отрасли выросла на 25,5%.

Динамика средней себестоимости единицы продукции в целом по отрасли складывается под влиянием двух факторов:

- изменения себестоимости единицы продукции на отдельном предприятии;

- структуры производства продукции отрасли.

Рассчитаем индекс фиксированного состава:

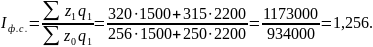
Таким образом, в результате повышения себестоимости единицы продукции на обоих предприятиях средняя себестоимость единицы выросла на 25,6%.

Определим влияние на среднюю себестоимость структурных сдвигов:

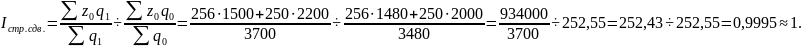
За изучаемый период структура производства практически не изменилась, поэтому изменение средней цены произошло целиком за счет влияния первого фактора, т.е. изменения себестоимости на производство продукции на каждом предприятии.

Правильность расчетов подтверждает проверка через взаимосвязь индексов:

7.4. Территориальные индексы

Территориальные индексы позволяют проводить сравнение одноименных показателей в территориальном разрезе. Например, сравнение цен на один и тот же вид продукции в разных городах, сравнение себестоимости одноименной продукции на разных заводах и т.д.

Для построения территориального индекса качественного показателя можно использовать два варианта расчета. Рассмотрим на примере.

Пример расчета территориальных индексов.

По имеющимся данным рассчитаем территориальный индекс цен физического объема и товарооборота (табл. 32).

Таблица 32

Сравнительная характеристика товарооборота Новосибирской и Томской областей

Вид продукции	Новосибирская область		Томская область
	цена, руб.	объем продаж, ед.	цена, руб.	объем продаж, ед.
А	25	50	28	45
В	40	95	42	105

Для расчета индекса цен в качестве весов можно использовать общий объем проданных товаров на двух территориях:

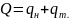
Тогда территориальный индекс будет выглядеть следующим образом:

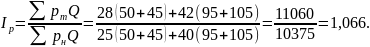
В Томской области цены на продукцию А и В выше, чем в Новосибирской, на 6,6%.

Можно также использовать второй способ расчета, при котором рассчитываются средние цены по каждому виду товара по двум территориям:

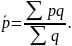
Для нашего примера:

=

=

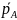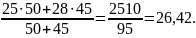
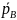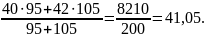
После этого рассчитаем территориальный индекс цен:

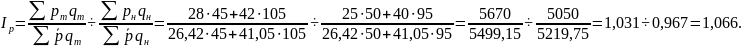
Индекс физического объема реализации будет строиться следующим образом:

=

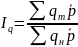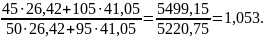
Таким образом, в Томской области объем продаж выше на 5,3%.

Общий индекс товарооборота найдем через взаимосвязь индексов:

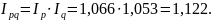
Общий товарооборот в Томской области выше, чем в Новосибирской области, на 12,2%.

Выводы

1. Индекс – это сравнение двух состояний одного явления. Наиболее часто проводятся сравнения во времени и пространстве.

2. Индексы могут быть индивидуальные и общие.

3. При построении общих индексов необходимо соблюдать правило построения индексов.

4. Агрегатные индексы используются в том случае, если изучается динамика показателя, который может быть представлен в виде произведения (товарооборот, общие затраты на производство продукции).

5. В зависимости от имеющихся данных агрегатные индексы могут быть преобразованы в средний гармонический и средний арифметический индексы.

6. Динамика средней величины характеризуется при помощи индексов переменного, постоянного состава и структурных сдвигов.

7. Сравнения в пространстве проводятся при помощи территориальных индексов.

8. Используя взаимосвязь между индексами, можно найти третий, зная значения двух других.

Глава 8. СТАТИСТИЧЕСКОЕ ИЗУЧЕНИЕ ВЗАИМОСВЯЗЕЙ

8.1. Статистическое изучение взаимосвязей, их классификация.

8.2. Задачи изучения взаимосвязей.

8.3. Понятие корреляционно-регрессионного анализа, условия его применения.

8.4. Показатели тесноты связи, линейный коэффициент корреляции.

8.5. Меры оценки тесноты связи для атрибутивных признаков.

8.1. Статистическое изучение взаимосвязей, их классификация

Статистическое изучение взаимосвязей является одним из важнейших разделов статистики. Изучение взаимосвязей между различными явлениями общественной жизни позволяет предсказывать развитие процессов, зависимых от других, и, в конечном счете, оказывать на них влияние.

Таким образом, изучение связей позволяет от объяснения фактов перейти к их изменению.

Взаимосвязь – это совместное согласованное изменение двух или нескольких признаков.

Присутствие взаимосвязи между различными явлениями, процессами выражается во взаимосогласованном изменении статистических данных, описывающих эти процессы.

Стаж работы является одним из факторов роста производительности труда, поэтому увеличение стажа, как правило, приводит к росту выработки. Статистические данные отражают согласованность в изменении обоих показателей.

Все многообразие взаимосвязей принято классифицировать по различным признакам [16]:

Форма проявления:

причинно-следственные связи – в том случае, когда из двух взаимодействующих признаков можно выделить причину и следствие, признак-фактор х и признак-результат у.

Взаимосвязь между объемом производимой продукции и себестоимостью единицы продукции проявляется следующим образом: с увеличением объема производимой продукции себестоимость единицы продукции снижается. В данном случае объем продукции – признак-фактор, а себестоимость – признак-результат.

Связи соответствия - в случае, когда нет возможности выделить причину и следствие, например: оба согласованно меняющихся признака являются следствиями третьего признака.

Механизм связи:

- функциональная;

- стохастическая (статистическая).

Под функциональной зависимостью между явлениями понимается такая связь, которая может быть выражена для каждого случая вполне определенно строгой математической формулой.

При функциональной зависимости каждому значению одной величины соответствует одно или несколько, но вполне определенных значений другой величины. Например, отношения между стороной и площадью квадрата (S=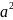 ), временем и путем при движении с постоянной скоростью (S=vt) и тому подобными величинами, часто встречающимися в геометрии, механике.

Для массовых социальных явлений характерны зависимости другого рода, возникающие в результате взаимодействия многих причин и условий и осложненные действием объективной случайности и ошибок наблюдения. Выразить подобные зависимости с помощью однозначных, точных формул, пригодных для описания каждого отдельного случая, невозможно.

При статистической связи разным значениям одной переменной соответствуют разные распределения значений другой переменной.

Частным случаем статистической связи является корреляционная связь.

Корреляционная зависимость – взаимосвязь между признаками, состоящая в том, что средняя величина значений одного признака меняется в зависимости от изменения другого признака (например, зависимость между выработкой и стажем работы, между числом судимости преступника и временем его нахождения на свободе и др.). Здесь, в отличие от функциональной зависимости, в индивидуальных случаях при определении значения одного признака могут быть разные значения другого, т.е. совсем не обязательно, что обнаруженная связь будет подтверждаться в каждом конкретном случае.

Изменение профессорско-преподавательского состава в сторону увеличения числа преподавателей, имеющих ученую степень, приводит в конечном итоге к повышению качества образования. Но это не значит, что каждый отдельно взятый выпускник будет обладать большим набором знаний, чем выпускник учебного заведения, имеющего более «слабый» преподавательский состав.

Следовательно, в статистическом анализе корреляционные зависимости проявляются не между каждой парой сопоставляемых данных, а между изменениями в рядах распределения множества соответствующих величин.

Кроме того, что корреляционная зависимость не имеет функционального характера, следует учитывать две ее особенности:

- вывод может быть сделан только на основе анализа достаточно больших статистических совокупностей, позволяющих построить относительно длинные статистические ряды;

- желательно, чтобы число наблюдений было не менее чем в 5-6 раз больше числа факторов [2].

Корреляционный анализ имеет смысл лишь в тех случаях, когда возможность причинной связи между анализируемыми признаками теоретически обоснована хотя бы на уровне содержательной гипотезы.

Если с изменением значения признака среднее значение другого признака не изменится закономерным образом, но закономерно изменятся другая статистическая характеристика (например, показатели вариации), то связь не является корреляционной, но является статистической.

В случае статистической связи предполагается, что оба признака имеют случайную вариацию индивидуальных значений относительно средней величины, т.е. каждый из признаков принимает несколько случайных значений. В том случае, если такую вариацию имеет один из признаков, а значения другого являются жестко детерминированными, говорят о регрессии, но не о статистической связи. При анализе динамических рядов можно измерять регрессию уровней ряда (имеющих случайную колеблемость) на номера лет: например, динамику производства продукции. Но нельзя говорить о корреляции (взаимосвязи) между выпуском продукции и временем и оценивать между ними тесноту связи.

Направление связи:

- прямая;

- обратная.

Если при увеличении признака-фактора растет признак-результат, говорят о прямой корреляционной связи. Например, чем выше ухоженность почвы, тем выше урожайность.

Если при увеличении признака-причины уменьшается признак-результат, говорят об обратной корреляционной зависимости. Например, чем выше социальный контроль в обществе, тем ниже преступность.

Форма связи:

- прямолинейная;

- криволинейная.

И прямые, и обратные связи могут быть прямолинейными и криволинейными. Математически прямолинейные связи могут быть описаны с помощью уравнения прямой:

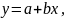
где y – признак-результат;

х– признак-фактор.

Криволинейные связи носят иной характер. Возрастание величины факторного признака оказывает неравномерное влияние на величину результативного признака.

Например, приведем связь преступлений с возрастом нарушителей. Вначале криминальная активность лиц растет прямо пропорционально увеличению возраста (приблизительно до 30 лет), а затем начинает снижаться. Математически такие связи описываются с помощью кривых (гиперболы, параболы).

Прямолинейные корреляционные связи могут быть однофакторными, когда исследуется связь между одним признаком-фактором и одним признаком-следствием (парная корреляция). Они могут быть многофакторными, когда исследуется влияние многих взаимодействующих между собой признаков-факторов на признак-следствие (множественная корреляция).