Динамика реализации продукции в отчетном периоде по сравнению с базисным

Наименование продукции	Реализация продукции, тыс. руб.			Изменение цен в текущем периоде по сравнению с базисным, %
	в базисном периоде	в отчетном периоде
Изделие 1	37000	35000	+4,0
Изделие 2	45500	45000	+2,8
Изделие 3	200	258	-2,0

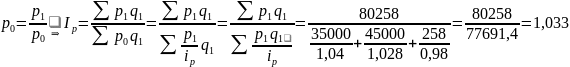
Таким образом, цены в отчетном периоде по сравнению с базисным увеличились на 3,3 %.

На основании имеющихся данных можно рассчитать индекс товарооборота:

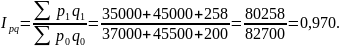
Общий товарооборот снизился на 3%.

Используя взаимосвязь между индексами, можно рассчитать индекс физического объема:

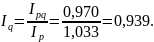
Результатом повышения цен явилось снижение объема продаж. Количество проданных изделий сократилось на 6,1%.

Пример расчета среднего арифметического индекса.

Имеются следующие данные о затратах на производство продукции (табл. 30). Как изменился объем произведенной продукции в стоимостном выражении?

Таблица 30

Динамика затрат на производство продукции

Наименование продукции	Общие затраты на производство продукции в базисном периоде, тыс. руб.	Изменение физического объема произведенной продукции в отчетном периоде по сравнению с базисным, %
Изделие А	23690	+3,5
Изделие В	2548	+5,5
Изделие С	12478	-2,1

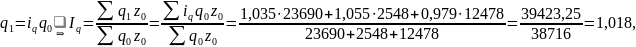
где 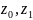- себестоимость единицы продукции соответственно в базисном и отчетном периоде.

Физический объем произведенной продукции в целом по предприятию увеличился на 1,8%.

7.3. Индексы средних величин

Индексы средних величин позволяют изучать динамику средних величин.

Как правило, такая потребность возникает в следующих случаях:

- если одна и та же продукция продается по различным ценам (на различных рынках);

- один и тот же вид продукции выпускается на различных предприятиях с различной себестоимостью;

- на производство одного и того же вида изделия затрачивается разное время;

- посевы одинаковой культуры имеют различную урожайность и т.д.

Динамика средней величины и факторы, ее формирующие, характеризуются с помощью системы индексов.

При этом определяют индексы:

- переменного состава;

- постоянного состава;

- структурных сдвигов.

Индекс переменного состава характеризует динамику средней величины и представляет собой отношение средней в отчетном периоде к средней величине базисного периода, рассчитанных по формуле средней арифметической взвешенной:

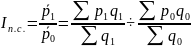–основная формула индекса переменного состава.

В данном случае p – цена, динамику средней которой мы ищем, а в качестве веса используется объем продаж – q.

В том случае, если есть структура продаж товара, применяют следующую формулу:

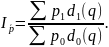
Здесь объем продаж представлен в виде удельного веса в общем объеме.

Изменение средней величины могут вызвать два фактора:

- изменение индивидуальной цены;

- изменение структуры продаж [12].

Влияние первого фактора отражает индекс постоянного (фиксированного) состава:

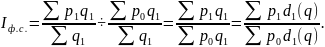
Влияние второго фактора отражает индекс структурных сдвигов:

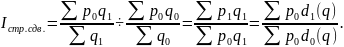
В предлагаемом примере рассмотрим индекс средней себестоимости единицы продукции.

Пример расчета индексов средних величин.

На предприятиях отрасли производится один вид продукции (табл. 31).

Таблица 31