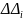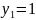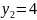- •Соян ш.Ч. Статистика
- •Содержание
- •Глава 1. Общие основы теории статистики……………………...5
- •Глава 2. Статистическое наблюдение……………………………..16
- •Глава 3. Сводка и группировка статистических материалов……………………………………………………………………29
- •Глава 1. Общие основы теории статистики
- •Понятие статистики.
- •Понятие статистики
- •Предмет статистики. Основные категории статистики
- •Структура статистической науки
- •1.4. Статистическая методология
- •1.5. Организация государственной статистики в
- •2.2. Организационные формы, виды и способы статистического наблюдения
- •2.3. Программно-методологические вопросы статистического наблюдения
- •2.4. Ошибки наблюдения
- •3.2. Виды группировок
- •3.3. Методологические вопросы проведения группировок. Особенности их решения для разных видов группировок
- •3.4. Практическое решение задач проведения группировок
- •Предварительная группировка фермерских хозяйств по размеру
- •Группировка фермерских хозяйств по размеру
- •Распределение числа малых предприятий Республики Тыва по отраслям экономики
- •Основные показатели деятельности промышленных предприятий
- •Предварительная группировка предприятий по объему производимой продукции
- •Аналитическая группировка предприятий
- •3.5. Ряды распределения
- •Распределение сотрудников фирмы по уровню образования
- •3.6. Система группировок
- •Глава 4.Статистические величины
- •Относительная величина планового задания:
- •Относительная величина выполнения плана:
- •Объем платных услуг населению Республики Тыва по видам
- •4.2. Понятие средней величины. Виды средних величин
- •Виды степенных средних величин
- •4.3. Правила выбора формы средних
- •Затраты на производство продукции
- •Группировка предприятий по уровню заработной платы
- •Характеристика выпускаемой продукции
- •4.4. Средняя арифметическая. Способы расчета средней арифметической
- •Группировка трехкомнатных квартир по стоимости
- •4.5. Структурные средние
- •Ряд распределения по среднедушевому доходу населения
- •Показатели вариации
- •Распределение семей по уровню среднедушевого дохода
- •5.3. Правило сложения дисперсии
- •Распределение магазинов по объему товарооборота
- •6.2. Ряды динамики, их классификация
- •6.3. Правила построения рядов динамики
- •6.4. Показатели анализа рядов динамики
- •Расчет показателей динамики
- •Численность трудовых ресурсов за ряд лет
- •Динамика выпуска продукции
- •6.5. Способы выравнивания динамических рядов. Экстраполяция и интерполяция
- •Производство продукции по месяцам
- •Производство продукции по кварталам
- •Сглаживание ряда динамики методом аналитического выравнивания
- •Производство продукции по месяцам
- •7.2. Агрегатная форма индексов
- •Данные для расчета индивидуальных и агрегатных индексов
- •Динамика реализации продукции в отчетном периоде по сравнению с базисным
- •Динамика затрат на производство продукции
- •7.3. Индексы средних величин
- •Динамика затрат на производство продукции
- •7.4. Территориальные индексы
- •Сравнительная характеристика товарооборота Новосибирской и Томской областей
- •8.2. Задачи изучения взаимосвязей
- •8.3. Понятие корреляционно-регрессионного анализа, условия его применения
- •Расчет параметров
- •8.4. Показатели тесноты связи, линейный коэффициент корреляции
- •8.5. Меры оценки тесноты связи для атрибутивных признаков
- •Данные для расчета коэффициентов Фехнера, Спирмена и Кендалла
- •Шкала оценки тесноты связи
- •Макет таблицы сопряженности 2х2
- •Зависимость уровня образования от пола
- •9.2. Способы формирования выборочной совокупности
- •9.3. Средняя и предельная ошибки выборки
- •Формулы определения средней ошибки для различных способов отбора
- •9.4. Использование результатов выборочного наблюдения
- •Глоссарий
- •Библиографический список
Производство продукции по месяцам
Месяц |
Производство продукции, млн. руб. |
Январь |
2500 |
Февраль |
2650 |
Март |
2500 |
Апрель |
2450 |
Май |
2550 |
Июнь |
2700 |
Июль |
2900 |
Август |
3100 |
Сентябрь |
3000 |
Октябрь |
3200 |
Ноябрь |
3100 |
Декабрь |
4000 |
Рассчитаем производство продукции по кварталам (табл.24).
Таблица 24
Производство продукции по кварталам
Квартал |
Производство продукции, млн. руб. |
I |
7650 |
II |
7700 |
III |
9000 |
IV |
10300 |
После проведенного укрупнения интервалов четко прослеживается тенденция к увеличению выпуска продукции к концу года.
Идея второго метода:
Для каждого уровня устанавливается средний из близлежащих уровней. Определяется трех-, пяти-, семизвенная и т.д. скользящие средние.
В общем виде пятизвенная средняя рассчитывается следующим образом:
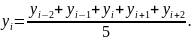
Аналогично рассчитываются трех- и семизвенные средние.
Пример использования метода скользящей средней.
Проведем сглаживание динамического ряда (табл.25) при помощи трех- и пятизвенной средних.
Таблица 25
Сглаживание динамического ряда методами трех- и пятизвенной средней
Месяц |
Производство продукции, млн. руб. |
Трехзвенная средняя |
Пятизвенная средняя |
Январь |
2500 |
- |
- |
Февраль |
2650 |
2550 |
- |
Март |
2500 |
2533 |
2530 |
Апрель |
2450 |
2500 |
2570 |
Май |
2550 |
2567 |
2620 |
Июнь |
2700 |
2717 |
2740 |
Июль |
2900 |
2900 |
2850 |
Август |
3100 |
3000 |
2980 |
Сентябрь |
3000 |
3100 |
3060 |
Октябрь |
3200 |
3100 |
3280 |
Ноябрь |
3100 |
3433 |
- |
Декабрь |
4000 |
- |
- |
Достоинство этого метода – простота и наглядность.
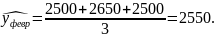
Наиболее эффективным методом выравнивания динамических рядов является аналитическое выравнивание, так как оно позволяет проводить интерполяцию и экстраполяцию, т.е. расчет прогнозных значений на перспективу или ретроспективу [6].
Идея третьего метода:
Уровни ряда представим в виде функции от времени, так как эмпирические точки можно представить в аналитическом виде множеством функций. Подбор функции, соответствующей тенденции, проводится на основе теоретического, качественного анализа. При этом необходимо учитывать возможность экономической интерпретации выбранной функции.
Рассмотрим три ситуации интерпретация которых легка:
- постоянный абсолютный прирост:
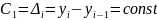
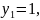
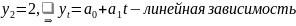
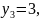
- постоянство вторых абсолютных разностей:
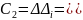
|
|
|
|
- |
- |
|
3 |
- |
|
5 |
2 |
|
7 |
2 |
|
9 |
2 |
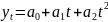 -
параболическая зависимость.
-
параболическая зависимость.
- постоянный цепной темп роста:
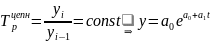 -
экспоненциальная
зависимость и т.д.
-
экспоненциальная
зависимость и т.д.
Подбор функции осуществляется также с помощью графического метода (см. тему «Статистическое изучение взаимосвязей»).
Для оценки параметров выбранного уравнения используют любой из трех методов: метод избранных точек, метод наименьших расстояний и метод наименьших квадратов (см. тему «Статистическое изучение взаимосвязей»).
Так,
например, для прямой
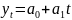 методом наименьших квадратов получим
следующие оценки параметров уравнения:
методом наименьших квадратов получим
следующие оценки параметров уравнения:
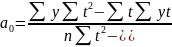
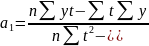
В рядах динамики техника расчета параметров уравнения может быть упрощена. Для этого показателям времени t придают такие значения, чтобы их сумма была равна нулю.
В этом случае параметры уравнения определяются следующим образом:
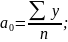
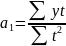
Если в динамическом ряду нечетное число уровней, то серединное значение времени принимают равным нулю, вверх, по убыванию, располагают по порядку отрицательные значения, вниз, по возрастанию, - положительные значения:
-5,-4,-3,-2,-1,0,1,2,3,4,5.
Если число уровней четное, то строят такой ряд:
-7,-5,-3,-1,1,3,5,7=0.
Пример использования метода аналитического выравнивания.
На основании данных табл.23 произведем сглаживание ряда динамики методом аналитического выравнивания (табл.26):
Таблица 26