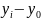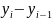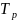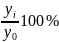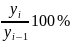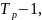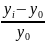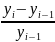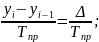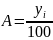- •Соян ш.Ч. Статистика
- •Содержание
- •Глава 1. Общие основы теории статистики……………………...5
- •Глава 2. Статистическое наблюдение……………………………..16
- •Глава 3. Сводка и группировка статистических материалов……………………………………………………………………29
- •Глава 1. Общие основы теории статистики
- •Понятие статистики.
- •Понятие статистики
- •Предмет статистики. Основные категории статистики
- •Структура статистической науки
- •1.4. Статистическая методология
- •1.5. Организация государственной статистики в
- •2.2. Организационные формы, виды и способы статистического наблюдения
- •2.3. Программно-методологические вопросы статистического наблюдения
- •2.4. Ошибки наблюдения
- •3.2. Виды группировок
- •3.3. Методологические вопросы проведения группировок. Особенности их решения для разных видов группировок
- •3.4. Практическое решение задач проведения группировок
- •Предварительная группировка фермерских хозяйств по размеру
- •Группировка фермерских хозяйств по размеру
- •Распределение числа малых предприятий Республики Тыва по отраслям экономики
- •Основные показатели деятельности промышленных предприятий
- •Предварительная группировка предприятий по объему производимой продукции
- •Аналитическая группировка предприятий
- •3.5. Ряды распределения
- •Распределение сотрудников фирмы по уровню образования
- •3.6. Система группировок
- •Глава 4.Статистические величины
- •Относительная величина планового задания:
- •Относительная величина выполнения плана:
- •Объем платных услуг населению Республики Тыва по видам
- •4.2. Понятие средней величины. Виды средних величин
- •Виды степенных средних величин
- •4.3. Правила выбора формы средних
- •Затраты на производство продукции
- •Группировка предприятий по уровню заработной платы
- •Характеристика выпускаемой продукции
- •4.4. Средняя арифметическая. Способы расчета средней арифметической
- •Группировка трехкомнатных квартир по стоимости
- •4.5. Структурные средние
- •Ряд распределения по среднедушевому доходу населения
- •Показатели вариации
- •Распределение семей по уровню среднедушевого дохода
- •5.3. Правило сложения дисперсии
- •Распределение магазинов по объему товарооборота
- •6.2. Ряды динамики, их классификация
- •6.3. Правила построения рядов динамики
- •6.4. Показатели анализа рядов динамики
- •Расчет показателей динамики
- •Численность трудовых ресурсов за ряд лет
- •Динамика выпуска продукции
- •6.5. Способы выравнивания динамических рядов. Экстраполяция и интерполяция
- •Производство продукции по месяцам
- •Производство продукции по кварталам
- •Сглаживание ряда динамики методом аналитического выравнивания
- •Производство продукции по месяцам
- •7.2. Агрегатная форма индексов
- •Данные для расчета индивидуальных и агрегатных индексов
- •Динамика реализации продукции в отчетном периоде по сравнению с базисным
- •Динамика затрат на производство продукции
- •7.3. Индексы средних величин
- •Динамика затрат на производство продукции
- •7.4. Территориальные индексы
- •Сравнительная характеристика товарооборота Новосибирской и Томской областей
- •8.2. Задачи изучения взаимосвязей
- •8.3. Понятие корреляционно-регрессионного анализа, условия его применения
- •Расчет параметров
- •8.4. Показатели тесноты связи, линейный коэффициент корреляции
- •8.5. Меры оценки тесноты связи для атрибутивных признаков
- •Данные для расчета коэффициентов Фехнера, Спирмена и Кендалла
- •Шкала оценки тесноты связи
- •Макет таблицы сопряженности 2х2
- •Зависимость уровня образования от пола
- •9.2. Способы формирования выборочной совокупности
- •9.3. Средняя и предельная ошибки выборки
- •Формулы определения средней ошибки для различных способов отбора
- •9.4. Использование результатов выборочного наблюдения
- •Глоссарий
- •Библиографический список
6.4. Показатели анализа рядов динамики
Для характеристики интенсивности изменения во времени в статистике используются следующие показатели:
- абсолютный прирост;
- темпы роста;
- темпы прироста;
- абсолютное значение 1% прироста.
Перечисленные показатели могут характеризовать динамику явления по отношению к предыдущему периоду, либо за интервал, включающий несколько периодов.
В соответствии с целью исследования различают цепные и базисные показатели динамики.
Если сравнение производится с периодом или моментом времени, начальным в ряду динамики, то имеют в виду базисный показатель динамики.
Если сравнение производится с предыдущим годом или моментом времени, то имеют в виду цепной показатель динамики.
Расчет показателей динамики приведен в табл.1.
Существует взаимосвязь между цепными и базисными абсолютными приростами и темпами роста (графа 3, табл.19). Если сложить все цепные абсолютные приросты, получим абсолютный базисный прирост за весь период (за который были рассчитаны цепные приросты). Если найти произведение цепных темпов роста, то получим базисный темп роста [1].
Таблица 19
Расчет показателей динамики
Показатель |
Базисный |
Цепной |
Взаимосвязь между ними |
1 |
2 |
3 |
4 |
|
|
|
|
|
|
|
|
|
|
|
- |
|
- |
|
- |
Помимо оценки интенсивности динамических процессов необходимо дополнить показатели динамики расчетом их средних, а именно:
- средний уровень ряда;
- средний абсолютный прирост;
- средний темп роста;
- средний темп прироста.
1. Методика расчета среднего уровня определяется видом ряда динамики.
Если ряд динамики интервальный, то считают по средней арифметической простой:
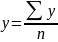
Если моментный ряд, то применяют среднюю хронологическую:
- простую, если моменты времени равно отстают (через год, месяц):
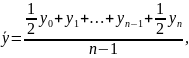
где n – число дат;
(n-1) – число периодов.
- взвешенную, если интервалы между датами различны, тогда формула выглядит следующим образом:
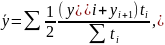
 -
продолжительность интервала от i-й
даты до даты i+1.
-
продолжительность интервала от i-й
даты до даты i+1.
Пример расчета средней хронологической взвешенной.
Имеются данные о численности трудовых ресурсов области за ряд лет (табл.20):
Таблица 20
Численность трудовых ресурсов за ряд лет
Показатель |
01.01.1989 г. |
01.01.1993 г. |
01.01.1994 г. |
01.01.1999 г. |
Трудовые ресурсы, млн. человек |
1,8 |
2,1 |
2,5 |
3,0 |
 =
=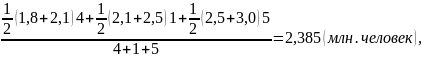
где - средняя годовая численность трудовых ресурсов.
Иногда рассчитывают по средней арифметической взвешенной, как:

где t– продолжительность интервала от одной даты до другой:
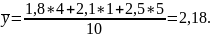
Расчет посредней арифметической является приближенным, так как используется не вся информация.
2. Средний абсолютный прирост может быть рассчитан как на основе цепных, так и базисных абсолютных приростов:
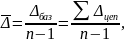
где n – число лет или дат.
3. Средний темп роста также рассчитывается либо на основе базисных, либо цепных темпов роста:
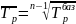 =
=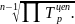
Темпы роста берутся в коэффициентах.
4.Средний темп прироста:
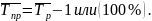
Пример расчета показателей динамики.
На основании имеющихся данных (табл.21) рассчитаем показатели, характеризующие динамику объема произведенной продукции и сделаем выводы.
Таблица 21
Выпуск продукции за 2005-2011 гг., млн. руб.
Показатель |
2005 г. |
2006 г. |
2007 г. |
2008 г. |
2009 г. |
2010 г. |
2011 г. |
Производство продукции, млн. руб. |
520,2 |
480,7 |
523,9 |
536,7 |
548,3 |
560,0 |
575,2 |
Результаты расчетов показателей динамики оформим в таблице 22.
Таблица 22