Распределение семей по уровню среднедушевого дохода
Средний душевой доход, руб. |
Число семей в группе |
|
|
|
|
До 2000 |
10 |
1500 |
-4 |
-40 |
160 |
2000-3000 |
35 |
2500 |
-3 |
-105 |
315 |
3000-4000 |
68 |
3500 |
-2 |
-136 |
272 |
4000-5000 |
70 |
4500 |
-1 |
-70 |
70 |
5000-6000 |
75 |
5500 |
0 |
0 |
0 |
6000-7000 |
30 |
6500 |
1 |
30 |
30 |
7000 и более |
12 |
7500 |
2 |
24 |
48 |
Итого |
300 |
|
|
-297 |
895 |
Как правило, в качестве константы Aвыбирается варианта с наибольшей частотой (для максимального упрощения расчетов). Наибольшая частота равна 75 – значитА=5500.
=
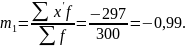
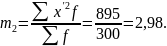
i
+ A
= 100 (-0,99) + 550 = 451.
=
(
-
)
=
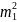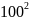(2,98 – (
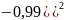= 19 999.
=
= 141,42.
V
=
100 % =
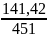100%
= 31,4 %.
На основании расчетов можно сделать вывод о том, что совокупность семей однородная. Однако коэффициент вариации приближается к верхней границе (33 %), превышение которой свидетельствует о неоднородности совокупности. Значит, в данной совокупности достаточно высокий уровень вариации.
Средний душевой доход по всей совокупности семей составляет 451 руб., а среднее отклонение от этого уровня – 141 руб. Поэтому можно констатировать достаточно высокую разницу между уровнем дохода отдельно взятых семей и, как следствие этого, начавшийся процесс расслоения общества. Дополнительные выводы можно сделать, рассчитав структурные средние – моду и медиану.
5.3. Правило сложения дисперсии
Если данные представлены в виде аналитической группировки, тогда в статистике рассматривают три вида дисперсии [13]:
общую;
среднюю из внутригрупповых;
межгрупповую.
Общая дисперсия измеряет вариацию признакаx во всей совокупности под влиянием всех факторов, обуславливающих эту вариацию.
Межгрупповая дисперсия (факторная) объясняет вариацию, вызванную признаком, положенным в основу группировки.
Средняя из внутригрупповых дисперсия (остаточная) объясняет ту часть вариации, которая вызвана действием (влиянием) на признак x всех остальных признаков (факторов), кроме группировочного.
Правило сложения дисперсии заключается в том, что общая дисперсия равна сумме межгрупповой и средней из внутригрупповых дисперсий:
=
+
,
где межгрупповая дисперсия;
средняя из внутригрупповых дисперсия.
Средняя из внутригрупповых рассчитывается в два этапа.
На первом этапе рассчитываются дисперсии по каждой группе как квадрат отклонений индивидуальных значений признака в группе от средней, рассчитанной в пределах группы:
=
;
=
;
=
.
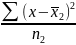где
численность i-й
группы.
На втором этапе по средней арифметической взвешенной рассчитывается средняя из внутригрупповых дисперсия:
=
.
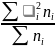Межгрупповая дисперсия определяется как квадрат отклонений средних, рассчитанных по каждой группе, от средней, рассчитанной в пределах всей совокупности, взвешенных численностью группы:
=
.
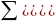Правильность расчетов дисперсии с помощью правила сложения дисперсии можно подтвердить расчетом общей дисперсии по обычной формуле.
Поскольку правило сложения дисперсии позволяет разложить дисперсию на дисперсию, возникающую под влиянием факторного признака (группировочного), и остаточную дисперсию, оно широко используется при изучении взаимосвязей между признаками.
На основе правила сложения дисперсии в статистике разработаны меры связей между факторным и результативными признаками: коэффициент детерминации и эмпирическое корреляционное отношение.
Коэффициент детерминации определяется как отношение межгрупповой дисперсии к общей дисперсии:
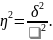
Коэффициент детерминации характеризует долю общей колеблемости результативного признака, которая вызвана признаком, положенным в основу группировки.
Эмпирическое корреляционное отношение характеризует тесноту связи между признаками и определяется следующим образом:
ŋ
=
=
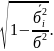
Пример использования правила сложения дисперсии.
Имеются данные о распределении магазинов по объему товароооборота (табл. 18).
Таблица 18