
- •Соян ш.Ч. Статистика
- •Содержание
- •Глава 1. Общие основы теории статистики……………………...5
- •Глава 2. Статистическое наблюдение……………………………..16
- •Глава 3. Сводка и группировка статистических материалов……………………………………………………………………29
- •Глава 1. Общие основы теории статистики
- •Понятие статистики.
- •Понятие статистики
- •Предмет статистики. Основные категории статистики
- •Структура статистической науки
- •1.4. Статистическая методология
- •1.5. Организация государственной статистики в
- •2.2. Организационные формы, виды и способы статистического наблюдения
- •2.3. Программно-методологические вопросы статистического наблюдения
- •2.4. Ошибки наблюдения
- •3.2. Виды группировок
- •3.3. Методологические вопросы проведения группировок. Особенности их решения для разных видов группировок
- •3.4. Практическое решение задач проведения группировок
- •Предварительная группировка фермерских хозяйств по размеру
- •Группировка фермерских хозяйств по размеру
- •Распределение числа малых предприятий Республики Тыва по отраслям экономики
- •Основные показатели деятельности промышленных предприятий
- •Предварительная группировка предприятий по объему производимой продукции
- •Аналитическая группировка предприятий
- •3.5. Ряды распределения
- •Распределение сотрудников фирмы по уровню образования
- •3.6. Система группировок
- •Глава 4.Статистические величины
- •Относительная величина планового задания:
- •Относительная величина выполнения плана:
- •Объем платных услуг населению Республики Тыва по видам
- •4.2. Понятие средней величины. Виды средних величин
- •Виды степенных средних величин
- •4.3. Правила выбора формы средних
- •Затраты на производство продукции
- •Группировка предприятий по уровню заработной платы
- •Характеристика выпускаемой продукции
- •4.4. Средняя арифметическая. Способы расчета средней арифметической
- •Группировка трехкомнатных квартир по стоимости
- •4.5. Структурные средние
- •Ряд распределения по среднедушевому доходу населения
- •Показатели вариации
- •Распределение семей по уровню среднедушевого дохода
- •5.3. Правило сложения дисперсии
- •Распределение магазинов по объему товарооборота
- •6.2. Ряды динамики, их классификация
- •6.3. Правила построения рядов динамики
- •6.4. Показатели анализа рядов динамики
- •Расчет показателей динамики
- •Численность трудовых ресурсов за ряд лет
- •Динамика выпуска продукции
- •6.5. Способы выравнивания динамических рядов. Экстраполяция и интерполяция
- •Производство продукции по месяцам
- •Производство продукции по кварталам
- •Сглаживание ряда динамики методом аналитического выравнивания
- •Производство продукции по месяцам
- •7.2. Агрегатная форма индексов
- •Данные для расчета индивидуальных и агрегатных индексов
- •Динамика реализации продукции в отчетном периоде по сравнению с базисным
- •Динамика затрат на производство продукции
- •7.3. Индексы средних величин
- •Динамика затрат на производство продукции
- •7.4. Территориальные индексы
- •Сравнительная характеристика товарооборота Новосибирской и Томской областей
- •8.2. Задачи изучения взаимосвязей
- •8.3. Понятие корреляционно-регрессионного анализа, условия его применения
- •Расчет параметров
- •8.4. Показатели тесноты связи, линейный коэффициент корреляции
- •8.5. Меры оценки тесноты связи для атрибутивных признаков
- •Данные для расчета коэффициентов Фехнера, Спирмена и Кендалла
- •Шкала оценки тесноты связи
- •Макет таблицы сопряженности 2х2
- •Зависимость уровня образования от пола
- •9.2. Способы формирования выборочной совокупности
- •9.3. Средняя и предельная ошибки выборки
- •Формулы определения средней ошибки для различных способов отбора
- •9.4. Использование результатов выборочного наблюдения
- •Глоссарий
- •Библиографический список
Показатели вариации
Показатели вариации являются необходимым дополнением при расчете средних величин, так как определяют степень однородности совокупности.
Показатели вариации включают:
размах вариации;
среднее абсолютное (линейное) отклонение;
среднее квадратическое отклонение;
дисперсию;
коэффициент вариации.
Значение показателей вариации:
характеризуют размеры вариации признак;
дополняют систему средних величин, в которой затушевываются индивидуальные различия;
позволяют охарактеризовать уровень однородности совокупности;
путем сравнения вариации у отдельных признаков (разных) помогают измерить взаимосвязь между этими признаками [4].
Первый показатель – размах вариации – наиболее простой из показателей. Он характеризует абсолютные размеры изменения признака и определяется как разница максимального и минимального значений признака:
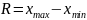
Несмотря на простоту расчета, этот показатель имеет недостаток: учитывает только два приграничных значения. В случае аномальности одного или двух приграничных значений он может исказить действительную вариацию совокупности.
Чтобы избавиться от этого недостатка, рассчитывают отклонение каждой индивидуальной величины от средней по совокупности. Таким образом, учитывается значение каждой единицы совокупности.
Чтобы охарактеризовать это отклонение одним числом, рассчитывают среднюю из этих значений. Данный показатель называется средним абсолютным (линейным) отклонением и определяется следующим образом:
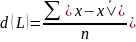 - простой вид;
- простой вид;
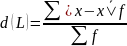 – взвешенный вид
– взвешенный вид
(для сгруппированных данных),
где d(L) – среднее абсолютное (линейное) отклонение;
x – индивидуальное значение признака (варианта);
– среднее из значений признака;
n – численность совокупности;
f – частота.
Среднее абсолютное (линейное) отклонение характеризует средний размер отклонений индивидуальных значений признака от средней величины . Таким образом, он характеризует абсолютные размеры вариации, имеет те же единицы измерения, что и признак, вариацию которого характеризует.
Недостаток показателя: ввиду того, что применяется модуль, затруднено проведение математических операций, поэтому он применяется редко.
Для того чтобы избавиться от недостатка предыдущего показателя, разницу между индивидуальным значением и средней возведем в квадрат и затем извлечем корень квадратный из полученного среднего значения. Полученный показатель называется средним квадратическим отклонением:
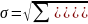 -
простой вид;
-
простой вид;
–взвешенный вид.
Этот показатель играет ту же роль, что и среднее абсолютное отклонение, но имеет перед ним одно преимущество, а именно – с ним проще проводить математические операции. Ввиду этого в 90 случаях из 100 используется этот показатель.
Еще более удобный для математических преобразований показатель вариации – дисперсия, которой представляет собой среднее квадратическое отклонение в квадрате:
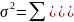 -
простой вид;
-
простой вид;
– взвешенный вид.
С помощью дисперсии и среднего квадратического отклонения измеряются взаимосвязи между различными признаками. Кроме того, по этим показателям можно сравнивать совокупности в смысле их однородности по одинаковым признакам.
Вывод об однородности совокупности позволяет сделать коэффициент вариации, который может быть рассчитан несколькими способами в зависимости от исходной информации:
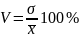 -
характеризует средний процент отклонений
индивидуальных значений признака от
средней величины.
-
характеризует средний процент отклонений
индивидуальных значений признака от
средней величины.
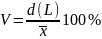 ,
,
 ,
,
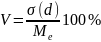 ,
,
где V - коэффициент вариации;
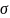 -
среднее квадратическое отклонение;
-
среднее квадратическое отклонение;
d (L) – среднее линейное отклонение;
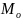 -
мода (структурная средняя);
-
мода (структурная средняя);
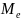 -медиана
(структурная средняя).
-медиана
(структурная средняя).
Коэффициент вариации имеет большое значение. Он позволяет сравнивать уровень вариации по различным признакам и используется для характеристики однородности совокупности. Если коэффициенты вариации меньше 33 %, то совокупность однородная.
Пример расчета показателей вариации.
Распределение студентов вуза по возрасту характеризуется следующими данными (табл. 16):
Таблица 16
Данные, характеризующие распределение студентов вуза по возрасту
Возраст студентов, лет |
Число студентов |
xi, лет |
|
Заочной формы обучения |
Дневной формы обучения |
||
17-20 |
5 |
60 |
18,5 |
20-23 |
36 |
120 |
21,5 |
23-25 |
48 |
90 |
24,0 |
25-28 |
52 |
55 |
26,5 |
28-30 |
80 |
10 |
29,0 |
30 и старше |
99 |
3 |
31,0 |
Рассчитайте показатели, характеризующие вариацию возраста студентов для каждой формы обучения. Сравните полученные результаты.
Рассчитаем показатели вариации, характеризующие совокупность студентов заочной формы обучения.
Размах вариации:
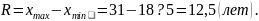
2. Средняя арифметическая:
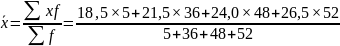
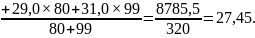
3. Среднее линейное отклонение:

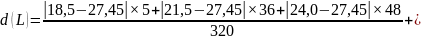

Возраст отдельно взятого студента отклоняется от среднего по совокупности возраста (27 лет) на 3 года. Значит, можно утверждать, что возраст наибольшего числа студентов не будет выходить за границы интервала: от 24,48 до 30,42 года.
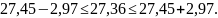
4. Среднее квадратическое отклонение:
=
Среднее квадратическое отклонение также характеризует абсолютную величину отклонения индивидуального значения от средней. Как правило, значение среднего квадратического отклонения больше среднего линейного отклонения.
Дисперсия:

Дисперсия характеризует квадрат отклонений индивидуального значения от средней величины.
Коэффициент вариации:
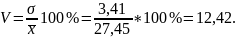
Средний процент отклонений индивидуальных значений от средней величины составляет 12,45%. Совокупность однородная.
Сделаем аналогичные расчеты по совокупности студентов дневной формы обучения. Получим следующие результаты:
R=12,5,
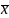 =
22,75,
=
22,75,
d(L) = 2.40,
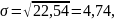
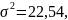
V= 21, 9%.
На основании расчетов можно сделать вывод о том, что совокупность студентов дневной формы обучения более однородная.
Расчет показателей вариации – достаточно трудоемкий процесс. В некоторых случаях, когда имеются некоторые показатели с равноотстоящими моментами времени или равноинтервальный ряд распределения, расчет может быть упрощен. Сокращенные способы расчета дисперсии базируются на знании свойств дисперсии [16].
Свойства дисперсии:
- если от всех значений варианты х отнять (прибавить) постоянное число А, то дисперсия не изменится;
-
если каждое значение варианты разделить
(умножить) на постоянную величину k,
то дисперсия уменьшится (увеличится) в
 раз.
раз.
Сокращённые способы расчета дисперсии:
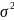 =
=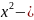
Способ моментов – применяется только в случае равенства интервалов.
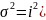 ),
),
где i – величина интервала;
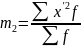 -
момент 2-го порядка.
-
момент 2-го порядка.
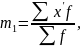
где
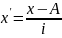 – момент 1-го порядка.
– момент 1-го порядка.
Пример расчета дисперсии способом моментов.
Имеются следующие данные о распределении семей по уровню среднедушевого дохода (табл. 17).
Таблица 17
