Группировка трехкомнатных квартир по стоимости

Стоимость квартир, тыс. руб.	Число квартир в группе f	x	x’	x’f
250-300	150	275	-2	-300
300-350	200	325	-1	-200
350-400	250	375	0	0
400-450	210	425	1	210
450-500	180	475	2	360
500-550	90	525	3	270
550-600	54	575	4	216
600-650	22	625	5	110
Итого	1156			666

Определим среднюю стоимость квартиры.

При использовании способа моментов удобнее всего результаты расчетов заносить в таблицу, для этого заранее в таблице резервируются три расчетные графы.

На основании данных табл. 14 рассчитываем момент 1-го порядка: итог по столбцу 5 делим на итог по столбцу 2.

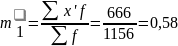
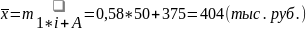
Средняя стоимость квартир, выставленных на продажу, составляет 404 (тыс. руб.).

Наряду со средней арифметической и средней гармонической, к другим степенным средним относится средняя геометрическая. В статистике она используется для осреднения темпов роста, коэффициентов динамики:

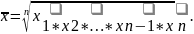
Средняя квадратическая используется при расчете показателей вариации, в частности – среднеквадратического отклонения, при исчислении средних ошибок выборки:

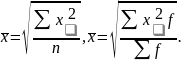
4.5. Структурные средние

Мода и медиана определяются структурой распределения. Они позволяют определить среднюю величину, без вычислений, визуально. Их используют в том случае, когда расчет степенных средних невозможен или нецелесообразен [27].

В дискретном ряду распределения мода определяется визуально.

Например, распределение семей по числу детей:

1 ребенок - 25

2 ребенка - 30

3 ребенка - 10

4 ребенка и более - 2

В дискретном ряду распределения мода равна 2, т.е. в данной совокупности наиболее часто встречаются семьи с 2 детьми. Очень удобно использовать этот показатель для характеристики наиболее часто встречаемого значения признака, определяемого по большей совокупности. Например, наиболее часто спрашиваемый размер обуви, размер одежды и т.д.

В интервальном ряду распределения, когда наиболее часто встречаемое значение признака задано в виде интервала, а мода должна отражать конкретное значение признака, используется следующая формула расчета:

,

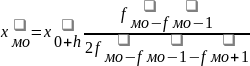где x_мо – мода;

x₀– верхняя граница модального интервала;

h – величина интервала;

f_{мо ,}f_мо-1,f_мо+1 – частоты модального, предмодального и послемодального интервалов.

В качестве модального берется интервал с наибольшей частотой.

Пример расчета моды по интервальному ряду распределения.

Имеется следующий ряд распределения по среднедушевому доходу населения (табл. 15):

Таблица 15

Ряд распределения по среднедушевому доходу населения

Интервал по среднедушевому доходу, руб.	Число семейfi	Накопленные частоты Si
1	2	3
До 1000	7	7
1000 – 1500	17	24
1500 – 2000	43	67
2000 – 2500	59	126
2500 – 3000	51	177
3000 – 3500	26	203
3500 – 4000	16	219
4000 – 4500	9	228
4500 – 5000	8	236
Итого	236	x

По данным табл. 15 видно, что наиболее часто встречаются семьи со среднедушевым доходом от 2000 до 2500 руб., т.е. наибольшей частоте (59) соответствует интервал 20000-25000. Данный интервал и будет модальным. Расчет по формуле позволяет получить более точное значение.

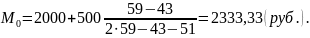
В данной совокупности наиболее часто встречается семьи со среднедушевым доходом 2333,33 руб.

Медиана – это варианта, которая делит ранжированный ряд распределения на две равные части. По обе стороны от медианы находится одинаковое число единиц совокупности. В дискретном ряду распределения медиана определяется визуально. Ряд признаков ранжируется, т.е. значения признаков упорядочиваются по возрастанию или убыванию. Варианта, которая делит упорядоченный ряд пополам, будет медианой [23].

Медиана в интервальном ряду распределения определяется по формуле:

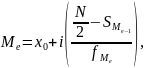
где 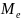- медиана;

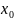- верхняя граница медианного интервала;

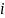- величина интервала;

N=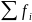 - общая численность;

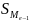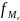- накопленные частоты предмедианного интервала;

- частота медианного интервала.

В качестве медианного берется интервал, в котором находится единица совокупности, которая делит упорядоченный по значению ряд пополам. Для того, чтобы определить медианный интервал, рассчитывают накопленные частоты. Последняя накопленная частота показывает общее количество единиц совокупности.

Пример расчета медианы (по данным табл. 15).

Последняя накопленная частота – 236. Медианный интервал должен содержать единицу совокупности, которая делит всю совокупность из 236 семей пополам (236/2=118). Значит, в качестве медианного в расчете будем брать интервал 2000-2500, так как среднедушевой доход до 2000 руб. имеют 67 семей из данной совокупности, т.е. менее половины совокупности. А интервалу 2000-2500 соответствует накопленная частота 126, значит, именно в этом интервале находится значение признака, которое разделит совокупность пополам, т.е. 118 семей будут иметь среднедушевой доход ниже медианного и 118 семей – выше медианного.

Произведем расчет медианы по формуле для интервального ряда:

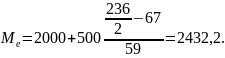
В изучаемой совокупности половина семей имеет доход ниже 2432,2 руб. на 1 человека.

Выводы

1. Различают три формы статистических величин: абсолютные, относительные, средние.

2. Относительные величины позволяют приводить данные в сопоставимый вид и производить сравнения, в то время как абсолютные величины характеризуют только абсолютные размеры явления и в сравнительных характеристиках применяются редко.

3. В статистической практике используются следующие виды относительных величин: планового задания, выполнения плана, динамики, координации, структуры, интенсивности, сравнения.

4. В статистических расчетах наиболее распространены средние величины, которые могут одним числом охарактеризовать всю совокупность при соблюдении условий расчета средней величины.

5. Различают два класса средних величин: степенные и структурные.

6. При расчете степенных средних для правильного выбора формулы расчета необходимо исходить из логической формулы расчета усредняемого показателя.

Глава 5. ПОКАЗАТЕЛИ ВАРИАЦИИ

5.1. Понятие вариации.

5.2. Показатели вариации.

5.3. Правило сложения дисперсии.

1. Понятие вариации

Вариация – это наличие различий у отдельных единиц совокупности по какому-либо признаку.

Эта категория занимает особое место в статистическом науке, ибо наличие вариации единиц совокупности предопределяет необходимость статистики. Если бы отдельные единицы совокупности имели одни и те же значения признаков (например, если рост, возраст у всех живущих людей были бы одинаковые), то для изучения данной совокупности по этим признакам достаточно было бы изучить только одну единицу совокупности. Однако зачастую значения признаков колеблются, изменяются при переходе от одной единицы к другой.

Как правило, вариация является порождением следующих причин:

• своеобразие условий, в которых происходит развитие отдельных единиц совокупности;

• неравномерность развития отдельных единиц.

Причинами вариации роста у отдельно взятых людей являются генетическая особенность каждого организма (основная причина), особенности питания, экологическая обстановка и т.д. Вариация урожайности может, вызвана климатическими, почвенными особенностями зоны произрастания, режима и возможности полива, качеством посадочного материала и т.д.

Вариация существует во времени и в пространстве.

Под вариацией в пространстве понимается колеблемость значений признака по отдельным территориям (урожайность пшеницы в разных регионах).

Под вариацией во времени подразумевается объективное изменение значений признака в разные периоды (или моменты). Например, со временем изменяется средняя продолжительность предстоящей жизни, доходность предприятий отрасли, уровень потребностей людей и т.д.

Вариация имеет важное значение в исследованиях, так как она характеризует степень однородности совокупности. Однородность совокупности – необходимое условие при расчете большинства статистических показателей, в частности средних величин [25].