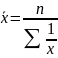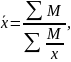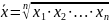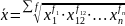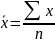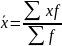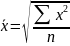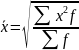Виды степенных средних величин

Вид средней	k	Простая средняя	Взвешенная средняя
Средняя гармоническая	k=-1	где n – численность совокупности	М=хf
Средняя геометрическая (Лопиталя)	k=0
Средняя арифметическая	k=1
Средняя квадратическая	k=2

Если рассчитать все виды средних для одних и тех же данных, то значения будут неодинаковыми: с увеличением показателя степени увеличивается соответствующая средняя величина.

4.3. Правила выбора формы средних

При изучении общественных явлений чаще всего используются средняя арифметическая и средняя гармоническая. Выбор средней в каждом конкретном случае зависит от характера связи между величиной осредняемого признака и другими признаками, характеризующими данное явление. Поэтому при выборе формы средней необходимо исходить из логической формулы расчета осредняемого показателя [22].

Рассмотрим на примерах 1-3, каким образом следует выбирать форму расчета средней величины.

Пример 1. Производственная деятельность предприятий отрасли характеризуется данными, представленными в табл. 11:

Таблица 11

Затраты на производство продукции

Предприятие	Общие затраты на производство, тыс. руб.	Затраты на 1 руб. произведенной продукции, коп.
1	6950	70
2	4800	75
3	5100	74
4	3200	70

Определим средние затраты на 1 руб. произведенной продукции в целом по отрасли.

В качестве варианты (х) будем рассматривать затраты на 1 руб. произведенной продукции, т.е. признак, значение которого будут осредняться.

Представим расчет этого показателя в виде логической формулы:

Затраты на 1 руб. произведенной продукции = Общие затраты на производство / Объем произведенной продукции.

Значения числителя (общие затраты на производство продукции) известны. Значения знаменателя могут быть определены на основании имеющихся данных:

Объем произведенной продукции = Общие затраты на производство продукции / Затраты на 1 руб. произведенной продукции.

Следовательно, средняя может быть рассчитана по формуле средней гармонической:

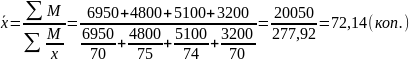
Пример 2. На основании имеющихся данных рассчитайте среднюю заработную плату на 1 работающего среди предприятий района (табл. 12).

Таблица 12

Группировка предприятий по уровню заработной платы

Группа предприятий по уровню заработной платы на 1 работающего, руб.	Число предприятий в группе	Фонд оплаты труда в среднем на 1 предприятие, тыс. руб.
До 1000	30	2500
1000-1100	28	3590
1100-1200	20	4260
1200 и выше	18	20000

Осредняемый признак – заработная плата на 1 работающего. Расчет осуществляется по следующей логической формуле:

Заработная плата на 1 работающего = Фонд оплаты труда (ФОТ) / Численность работающих.

Поскольку мы считаем среднюю заработную плату по всем предприятиям, расчет средней заработной платы будет произведен по следующей формуле:

Средняя заработная плата = Общий фонд оплаты труда по всем предприятиям / Общая численность работающих на всех предприятиях.

В исходной формуле числитель (общий ФОТ) может быть найден следующим образом:

Общий ФОТ по всем предприятиям = ФОТ в среднем на 1 предприятие ∙ Число предприятий в группе.

При расчете знаменателя (численность работающих) используем данные предыдущего расчета:

Численность работающих = Общий ФОТ по всем предприятиям / заработная плата на 1 работающего.

Расчет средней осуществляется по формуле средней гармонической взвешенной. При расчете учитываем, что значения признака представлены в виде интервалов, поэтому необходимо установить центры интервалов. Берем полусумму каждого интервала (его центр), считая, что этот центр является средней, характеризующей всю совокупность величин, находившихся в данном интервале. В расчете будут использованы середины интервалов:

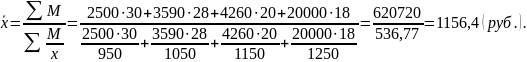
Пример 3. Имеются следующие данные, характеризующие качество выпускаемой продукции (табл. 13).

Определим средний процент бракованной продукции по всем видам изделий.

Таблица 13