
- •2. Понятие «жидкость». Капельная, реальная, идеальная, упругая жидкость. Силы, действующие в жидкости.
- •4. Гидростатическое давление (гд). Два основных свойства гд (с доказательством).
- •5. Гидростатическое давление: атмосферное, избыточное, вакууметрическое, абсолютное.
- •Эксцентриситет
- •Определение
- •Центр величины ц ентр водоизмещения — Центр объема жидкости, вытесненной плавающим телом в связанной с ним системе отсчета
- •Метацентр
- •Метацентрическая высота
- •Запас плавучести
- •13. Уравнение неразрывности потока. Вывод уравнения. Применение уравнения к решению практических задач.
- •15. Геометрических смысл уравнения Бернулли. Энергетический смысл уравнения Бернулли. Полный напор. Напорная и пьезометрическая линии.
- •16. Гидравлические элементы живого сечения (площадь живого сечения, длина смоченного периметра, гидравлический радиус). Два режима движения жидкости (ламинарный и турбулентный).
- •17. Опыты о.Рейнольдса. Критические числа Рейнольдса. Определение числа Рейнольдса.
1. История развития дисциплины. Труды Архимеда, Леонардо да-Винчи. Вклад в развитие науки Ньютона, Паскаля, Торичелли. Работы Ломоносова, Бернулли, Эйлера. Исследования Н.Жуковского. Наши современники и их вклад в развитие дисциплины. Исторически сложилось так, что развитие гидромеханики, как у нас, так и за рубежом шло по двум направлениям: ☼ первый путь – теоретический, путь точного математического анализа, основанного на законах механики. Он привел к созданию теоретической гидромеханики, которая долгое время являлась самостоятельной дисциплиной не связанной с экспериментом. Однако на пути чисто теоретического исследования движения жидкости встречается много трудностей, и методы теоретической гидромеханики не всегда дают ответы на вопросы, выдвигаемые практикой. ☼ второй путь – путь широкого эксперимента и накопления опытных данных для использования их в инженерной практике – привёл к созданию технической гидромеханики или гидравлики. Этот путь возник из насущных задач практической инженерной деятельности людей. В начальный период своего развития гидравлика была наукой чисто электрической. В настоящее же время в ней, где это возможно и целесообразно, всё больше применяют методы теоретической гидромеханики для решения отдельных задач, а теоретическая гидромеханика всё чаще начинает прибегать к эксперименту как к критерию достоверности своих выводов. Таким образом, различие в методах этих двух направлений одной и той же науки постепенно исчезает. Из сказанного выше видно, что термины «Техническая гидромеханика», «Техническая механика жидкости» и «Гидравлика» следует рассматривать как имеющие одинаковое значение (как бы синонимы). Гидравлика – очень древняя наука. За несколько тысяч лет до нашей эры в Индии, Китае, в Египте, странах Ближнего и Среднего востока уже строились различные гидротехнические сооружения: каналы, платины, водяные колеса. Методов расчета этих сооружений в то время не существовало и определенные достижения в гидротехническом строительстве были возможны благодаря искусству и практическому опыту строителей. Первым научным трудом в области гидравлики считается написанный примерно за 250 лет до н.э. трактат Архимеда «О плавающих телах», в котором величайший ученый древности сформулировал закон о давлении жидкости на погруженное в нее тело. Особое развитие гидравлика получила в средние века. В XVвеке Леонардо да Винчи написал труд «О движении и измерении воды в тесных сооружениях», опубликованный через 307 лет после его смерти в 1826 году. В 1586 году голландский ученый Симон Стевин опубликовал работу «Начало гидростатики». В XVI – XVII веках Г. Галилей, Э. Торичелли, Б. Паскаль и И. Ньютон проводили исследования, позволившие разработать основы гидромеханики. В 1755 – 1756 годах выходят в свет работы Л.П. Эйлера, где впервые приводится полная система дифференциальных уравнений равновесия и движения идеальной ж. Основоположниками гидравлики как самостоятельной науки являются члены Петербургской академии наук М.В. Ломоносова, Д.И. Бернулли, Л.П. Эйлер.
3. Механические характеристики жидкости. Физические свойства капельной жидкости (сжимаемость, вязкость, поверхностное натяжение, температурное расширение, капиллярность, испаряемость, растворимость газов.) Плотностью -называется количество покоящейся массы данного вещества, заключенного в единице его объема. ρ=m/V (кг/м3) относительная плотность-соотношение плотности в-ва к плотности воды при -4 0 С Удельный вес – вес единицы объема жидкости γ=G/V (H/ м3), γ=ρg; G вес жидкости в объеме V Удельный объем – объем единицы массы покоящейся жидкости υ=1/ρ (м3/кг) Текучесть - это легкоподвижность частиц жидкости, обусловловленная ее неспособностью воспринимать касательные напряжения в состоянии покоя. Поэтому жидкость не может сохранять собственную форму, а принимает форму сосуда (резервуара, водоема), в котором находится. Сжимаемость - способность жидкостей уменьшать объем при увеличении давления. Характеризуется коэффициентом объемного сжатия βW, который представляет собой относительное изменение объема жидкости на единицу изменения давления: βW = - ΔV/VΔp, гдеV - первоначальный объем жидкости; ΔV - приращение (изменение) этого объема при увеличении давления на величинуΔρ .Коэффициент объемного сжатия в системе СИ имеет размерность Па-1. Знак минус в этой формуле обусловлен тем, что положительному приращению давления ρ соответствует отрицательное приращение (т.е. уменьшение) объема жидкости. Вязкость жидкостей - свойство жидкости сопротивляться относительному движению (сдвигу) ее частиц, обусловливающее появление силы внутреннего трения между слоями жидкости, если последние имеют различные скорости движения.( св-во обратное текучести). Это свойство характеризуется коэффициентами динамической μ и кинематической ν вязкостей. μ= τ/du*dy, Где τ-сила, которая возникает на единице площади поверхности двух движущихся друг относительно друга слоев жидкости при градиенте скорости равный 1 (du -разность скоростей перемещающихся слоев воды, dy - толщина слоя). В международной системе единиц динамическая вязкость выражается в Н*с/м2 или Па*с В практике для характеристики вязкости жидкости чаще применяют не коэффициент динамической вязкости, а коэффициент кинематической вязкости ν (м2/с или Стокс). 1 Ст=1 м2/с. Коэффициентом кинематической вязкости называется отношение коэффициента динамической вязкости к плотности жидкости: ν=μ/ρ, Вязкость капельных жидкостей при увеличении температуры уменьшается, а вязкость газов возрастает Сила поверхностного натяжения - это сила, обусловленная взаимным притяжением молекул жидкости, направленная по касательной к ее поверхности. Силы, действующие на поверхности раздела газ-жидкость, стремятся придать малому объему жидкости сферическую форму : Ep = Aвнеш = σS, Ep -потенциальной энергией, ΔAвнеш-работa внешних сил, S- площади поверхности, σ-коэффициент поверхностного натяжения(1 Н/м = 1 Дж/м2) σ= FH/2L Δρ=2σ/r(для мыльного пузыря) Δρ-избыточное давление, σ-коэф. поверхностного натяжения, r-радиус; Δρ=4σ/r (капля жидкости) Температурное расширение - способность 5. Гидростатическое давление: атмосферное, избыточное, вакууметрическое, абсолютное. Давление в жидкости измеряется приборами: пьезометрами, манометрами, вакуумметрами. Пьезометры и манометры измеряют избыточное (манометрическое) давление, то есть они работают, если полное давление в жидкости превышает величину, равную одной атмосфере p = 1 кгс/см2 = 0,1 МПа. Эти приборы показывают долю давления сверх атмосферного. Для измерения в жидкости полного давления p необходимо к манометрическому давлению pман прибавить атмосферное давление pатм, снятое с барометра. Практически же в гидравлике атмосферное давление считается величиной постоянной pатм= =101325 100000 Па.
Пьезометр обычно
представляет собой вертикальную
стеклянную трубку, нижняя часть
которой сообщается с исследуемой
точкой в жидкости, где нужно измерить
давление (например, точка А на рис. 2),
а верхняя её часть открыта в атмосферу.
Высота столба жидкости в пьезометре
hp
является показанием этого прибора
и позволяет измерять избыточное
(манометрическое) давление в точке по
соотношению
где hp — пьезометрический напор (высота), м. Упомянутые пьезометры применяются главным образом для лабораторных исследований. Их верхний предел измерения ограничен высотой до 5 м, однако их преимущество перед манометрами состоит в непосредственном измерении давления с помощью пьезометрической высоты столба жидкости без промежуточных передаточных механизмов. В качестве пьезометра может быть использован любой колодец, котлован, скважина с водой или даже любое измерение глубины воды в открытом резервуаре, так как оно даёт нам величину hp .
Манометры
чаще всего
применяются механические, реже —
жидкостные. Все манометры измеряют
не полное давление, а избыточное
Преимуществами их перед пьезометрами являются более широкие пределы измерения, однако есть и недостаток: они требуют контроля их показаний. Манометры, выпускаемые в последнее время, градуируются в единицах СИ: МПа или кПа (см. на с. 54). Однако ещё продолжают применяться и старые манометры со шкалой в кгс/см2, они удобны тем, что эта единица равна одной атмосфере (см. с. 8). Нулевое показание любого манометра соответствует полному давлению p, равному одной атмосфере. Вакуумметр по своему внешнему виду напоминает манометр, а показывает он ту долю давления, которая дополняет полное давление в жидкости до величины одной атмосферы. Вакуум в жидкости — это не пустота, а такое состояние жидкости, когда полное давление в ней меньше атмосферного на величину pв, которая измеряется вакуумметром. Вакуумметрическое давление pв, показываемое прибором, связано с полным и атмосферным так:
6.Основное уравнение гидростатики (вывод). Закон Паскаля. Гидростатический парадокс. Героновы фонтаны, устройство, принцип действия.
Основное
уравнение гидростатики
гласит, что полное давление в жидкости
p
равно сумме внешнего давления на
жидкость po
и давления веса столба жидкости pж,
то есть:
В частном случае
для открытых резервуаров, сообщающихся
с атмосферой (рис. 2), внешнее
давление на жидкость равно атмосферному
давлению po
= pатм
= 101325 Па
Избыточное давление (манометрическое) есть разность между полным и атмосферным давлением. Из последнего уравнения получаем, что для открытых резервуаров избыточное давление равно давлению столба жидкости
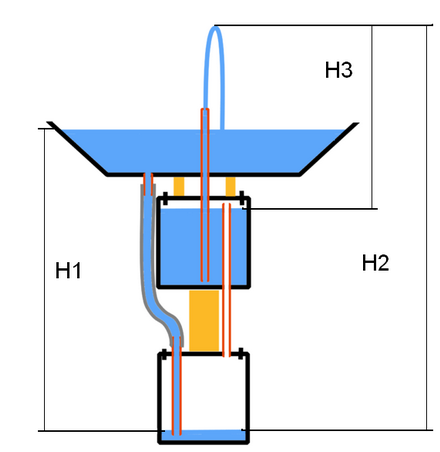
З Гидростатический парадокс - свойство жидкостей, заключающееся в том, что сила тяжести жидкости, налитой в сосуд, может отличаться от силы, с которой эта жидкость действует на дно сосуда. Героновы фонтаны. Знаменитый ученый древности Герон Александрийский придумал оригинальную конструкцию фонтана, которая находит применение и в наши дни. Главное чудо этого фонтана заключалось в том, что вода из фонтана била сама, без использования, какого либо внешнего источника воды. Принцип работы фонтана хорошо виден на рисунке. Схема устройства фонтана Герона Геронов фонтан состоит из открытой чаши и двух герметичных сосудов расположенных под чашей. Из верхней чаши в нижнюю емкость, идет полностью герметичная трубка. Если налить в верхнюю чашу воды, то вода по трубке начинает стекать в нижнюю емкость, вытесняя оттуда воздух. Поскольку сама нижняя емкость полностью герметична, то воздух выталкиваемый водой, по герметичной трубке, передает воздушное давление в среднюю чашу. Давление воздуха в средней емкости начинает выталкивать воду, и фонтан начинает работать. Если для начала работы, в верхнюю чашу требовалось налить воды, то для дальнейшей работы фонтана, уже использовалась вода 8.Дифференциальные уравн. покоящейся идеальной жидкости (Уравнения Л.Эйлера). Вывод уравнений, пример применения уравнений для решения практических задач.
|
В 1738 году была опубликована работа Д. Бернулли «Гидравлика или записки о силах движения жидкости», в которой установлена зависимость между давлением и скоростью в элементарной струйке идеальной жидкости. Представляют интерес такие работы Шизе, Вентури, Вейсбаха, Дарси, Базена и Рейнольдса. Труды этих ученых посвящены главным образом изучению турбулентности потоков и установлению общих законов сопротивления движению вязких жидкостей, а также исследованию движения жидкости в трубах, каналах и на водосливах. Большое внимание уделено в них также разработке теории размерности и подобия и постановке лабораторных экспериментов. В 1791 году вышла в свет первое русское руководство по гидравлике А. Колмакова «Карманная книжка для вычисления количества воды, вытекающей через трубы, отверстие или по желобам, также и силы, какой они ударяют, стремясь с данной скоростью». В конце XIX – начала XX века появились работы русских ученных: И.С. Громека, предположившего уравнения вихревого движения жидкости; Н.П. Петрова, разработавшего гидродинамическую теорию смазки; Н.Е. Жуковского, создавшего теорию гидравлического удара в трубах. Большой вклад в развитие гидравлики принесли советские ученые: А.Н.Колмогоров (теория турбулентности), Н.Н Павловский (теория фильтрации, равномерное и неравномерное движение жидкости), И.Н. Куколевский (теория машиностроительной гидравлики), С.А.Христианович (неустановившиеся движения жидкости) и многое другие.
жидкостей изменять объем при изменении температуры. Для капельных жидкостей характеризуется коэффициентом температурного расширения βT , равным относительному изменению объема при изменении температуры t на один градус при постоянном давлении: βT= ΔV/VΔt, где V- первоначальный объем; ΔV- изменение этого объема при повышении температуры на величину Δt.Коэффициент температурного расширения в системе СИ имеет размерность град-1.Коэффициент зависит для данной жидкости от температуры и давления. Капиллярными явлениями называют подъем или опускание жидкости в трубках малого диаметра – капиллярах. Смачивающие жидкости поднимаются по капиллярам, несмачивающие – опускаются. h=2σcosθ/ρgr При полном смачивании θ = 0, cos θ = 1 h=2σ/ρgr=4σ/γd, θ-угол смачивания, ρ-плотность, γ-удельный вес, Испаряемость жидкостей. При повышении температуры жидкости и, в некоторых случаях, при снижении давления часть массы капельной жидкости постепенно переходит в газообразное состояние (пар). Интенсивность процесса парообразования зависит от температуры кипения жидкости при нормальном атмосферном давлении: чем выше температура кипения жидкости, тем меньше её испаряемость. Однако, чем больше насыщенность паров при данной температуре, тем больше испаряемость жидкости. Растворение газов - способность жидкости поглощать (растворять) газы, находящиеся в соприкосновении с ней. Все жидкости в той или иной степени поглощают и растворяют газы. Это свойство характеризуется коэффициентом растворимости kр. VГ/ Vж = kр P1 / P2 где VГ– объём растворённого газа при нормальных условиях, Vж– объём жидкости, P1 и P2– начальное и конечное давление газа. Коэффициент растворимости зависит от типа жидкости, газа и температуры.
1 ат, то есть предельное значение pв 100000 Па, так как полное давление не может быть меньше абсолютного нуля. Приведём примеры снятия показаний с приборов: — пьезометр, показывающий hp=160 см вод. ст., соответствует в единицах СИ давлениям pизб=16000 Па и p= 100000+16000=116000 Па; — манометр с показаниями pман = 2,5 кгс/см2 соответствует водяному столбу hp=25 м и полному давлению в СИ p = 0,35 МПа;
— Е сли давление Р отсчитывают от абсолютного нуля, то его называют абсолютным давлением Рабс. Если давление отсчитывают от атмосферного, то оно называется избыточным (манометрическим) Ризб. Оно измеряется манометром. Атмосферное давление постоянно Ратм = 103 кПа (рис.1.5). Вакуумметрическое давление Рвак - недостаток давления до атмосферного
попадавшая в чашу из средней емкости. Как видно устройство фонтана очень простое, но это только на первый взгляд. Подъем воды в верхнюю чашу осуществляется за счет напора воды высотой H1, при этом воду фонтан поднимает на гораздо большую высоту H2, что на первый взгляд кажется невозможным. Ведь на это должно потребоваться гораздо большее давление. Фонтан не должен работать. Но знание древних Греков оказалось столь высоко, что они догадались передавать давление воды из нижнего сосуда, в средний сосуд, не водой, а воздухом. Поскольку вес воздуха значительно ниже веса воды, потери давления на этом участке получаются очень незначительными, и фонтан бьет из чаши на высоту H3. Высота струи фонтана H3, без учета потерь давления в трубках, будет равна высоте напора воды H1. Таким образом, чтобы вода фонтана била максимально высоко, необходимо как можно выше сделать конструкцию фонтана, тем самым увеличив расстояние H1. Кроме того, нужно как можно выше поднять средний сосуд. Что касается закона физики о сохранении энергии, то он полностью соблюдается. Вода из среднего сосуда, под действием гравитации стекает в нижний сосуд. То, что она проделывает этот путь через верхнюю чашу, и при этом бьет там фонтаном, ни сколько не противоречит закону о сохранении энергии. Когда вся вода из среднего сосуда, перетечет в нижний, и фонтан перестанет работать.
7. недостаток: они требуют контроля их показаний. Манометры, выпускаемые в последнее время, градуируются в единицах СИ: МПа или кПа. Однако ещё продолжают применяться и старые манометры со шкалой в кгс/см2, они удобны тем, что эта единица равна одной атмосфере. Нулевое показание любого манометра соответствует полному давлению p, равному одной атмосфере. Вакуумметр по своему внешнему виду напоминает манометр, а показывает он ту долю давления, которая дополняет полное давление в жидкости до величины одной атмосферы. Вакуум в жидкости — это не пустота, а такое состояние жидкости, когда полное давление в ней меньше атмосферного на величину pв, которая измеряется вакуумметром. Вакуумметрическое давление pв, показываемое прибором, связано с полным и атмосферным так: . Величина вакуума pв не может быть быть больше 1 ат, то есть предельное значение pв 100000 Па, так как полное давление не может быть меньше абсолютного нуля. Приведём примеры снятия показаний с приборов: — пьезометр, показывающий hp=160 см вод. ст., соответствует в единицах СИ давлениям pизб=16000 Па и p= 100000+16000=116000 Па; — манометр с показаниями pман = 2,5 кгс/см2 соответствует водяному столбу hp=25 м и полному давлению в СИ p = 0,35 МПа; — вакуумметр, показывающий pв=0,04 МПа, соответствует полному давлению p=100000-40000=60000 Па, что составляет 60 % от атмосферного.
|
2. Понятие «жидкость». Капельная, реальная, идеальная, упругая жидкость. Силы, действующие в жидкости. Жидкость легко подвижная среда, заполняющая объем без пустот и промежутков. Жидкостью называют физическое тело, обладающее весьма большой подвижностью частиц, текучестью. Различают два вида жидкостей: капельные и газы. Капельные жидкости оказывают большое сопротивление изменению объема и трудно поддаются сжатию .(мало изменяют объем при изменении давления, легко принимают любую форму резервуара). Газы легко меняют объем при изменении давления и температуры, и имеют значительно меньшую плотность, чем капельные жидкости. В гидравлике различают жидкости реальные и идеальные. К идеальным относятся жидкости абсолютно не меняющие объем (несжимаемые), невязкие.(обладает текучестью, предложил Эйлер). Реальной жидкостью считается жидкость вязкая сжимаемая или несжимаемая.(обладает текучестью, вязкостью, сжимаемостью) В основном в гидравлике рассматриваются вязкие несжимаемые жидкости. Упругая жидкость, которую называют жидкостью Максвелла (а также телом или моделью Максвелла). Эта жидкость не подчиняется закону вязкости Ньютона и поэтому называется неньютоновской жидкостью. В гидравлике рассматривается два типа сил, действующих в жидкости: массовые и поверхностные. Массовые силы обусловлены действующим на жидкость силовым полем, они приложены к каждой частице жидкости и пропорциональны их массе, примером таких сил являются силы тяжести(G=mg), силы инерции переносного движения (Fин=ma). Поверхностные силы обусловлены взаимодействием рассматриваемого объема с окружающими его телами; силы реакции стенок сосуда; если рассматривается объем, мысленно выделенный из общей массы жидкости – это силы, действующие на него со стороны «отброшенной» жидкости, распределенные по поверхности объема и пропорциональны площади поверхности, на которую они действуют.(сила давления Р=РF/S, РF-поверхност. силы, S –площадь поверхности; сила трения τ= T/ω, T-касательная сила ,ω-площадь) Рпов=2σ/r; Pпов- напряжения в жидкости,σ - коэффициент поверхностного натяжения, r - радиус сферической поверхности, которую принимает жидкость. Δh=4σ/gdρ=k/d d – диаметр капилляра, k – коэффициент пропорциональности k=4σ/gρ
4. Гидростатическое давление (ГД). Два основных свойства ГД (с доказательством). Гидростатикой называется раздел гидравлики, в котором рассматриваются законы равновесия жидкости и их практическое применение. В покоящейся жидкости всегда присутствует сила давления, которая называется гидростатическим давлением. Жидкость оказывает силовое воздействие на дно и стенки сосуда. Частицы жидкости, расположенные в верхних слоях водоема, испытывают меньшие силы сжатия, чем частицы жидкости, находящиеся у дна. Pср =ΔP/ΔS
П Рассмотрим силу гидростатического давления Р, приложенную в точке С под углом к поверхности А—В объема жидкости, находящегося в покое. Тогда эту силу можно разложить на две составляющие: нормальную Рп и касательную Рt к поверхности А—В. Касательная составляющая—это равнодействующая сил трения, приходящихся на выделенную поверхность вокруг точки С. Но так как жидкость находится в покое, то силы трения отсутствуют, т. е. Рt =0. Следовательно, сила гидростатического давления Р в точке С действует лишь в направлении силы Рп, т. е. нормально к поверхности А—В. Причем направлена она только по внутренней нормали. При предположении направления силы гидростатического давления по внешней нормали возникнут растягивающие усилия, что приведет жидкость в движение. А это противоречит условию. Таким образом, сила гидростатического давления всегда сжимающая, т. е. направлена но внутренней нормали.
В Для доказательства этого свойства выделим в жидкости, находящейся в равновесии, частицу в форме 4 треугольной призмы с основанием в виде прямоугольного треугольника А—В—С. Будем рассматривать этот объём в некоторой произвольной системе координат X,Y,Z. При этом ось у перпендикулярна плоскости. Заменим 4.действие жидкости вне призмы на ее боковые грани гидростатическим давлением соответственно Pх, Pz, Pе. Px=px*dz*dy Pz=pz*dx*dy Pe=pe*de*dy Кроме этих сил на призму действует сила тяжести dG, равная весу призмы g*dz*dx*dy/2. Силой тяжестью можно пренебречь. Так как она будет величиной 3-го порядка малости, а силы действующие на грани призмы 2 –го порядка малости. Так как частица жидкости находится в равновесии, в покое, то сумма проекций всех сил, приложенных к ней, на любое направление равна нулю т.е. ∑x=0; px*dz*dy- pe*de*dy*sinα=0 ∑z=0; pz*dx*dy- pe*de*dy*cosα=0 Подставляя dz=de sina и dx=de cosa в предыдущие уравнения и разделив каждое уравнение dy, получим ∑x=0; px*dz - pe*dz =0 ∑z=0; pz*dx - pe*dx =0 , Из выражений следует px= pz= pe Следовательно, гидростатическое давление на наклонную грань Ре одинаково по величине с гидростатическим давлением на вертикальную и горизонтальную грани. Так как угол наклона грани a взят произвольно, то можно утверждать, что гидростатическое давление в любой точке жидкости действует одинаково по всем направлениям. Свойство 3. Гидростатическое давление в точке зависит от ее координат в пространстве. Это положение не требует специального доказательства, так как ясно, что по мере увеличения погружения точки давление в ней будет возрастать, а по мере уменьшения погружения уменьшаться. P = f (x, y, z)
7. Приборы, применяемые для измерения давления (атмосферного, избыточного, вакууметрического). Устройство, принцип действия. Класс точности приборов. Давление в жидкости измеряется приборами: пьезометрами, манометрами, вакуумметрами. Пьезометры и манометры измеряют избыточное (манометрическое) давление, то есть они работают, если полное давление в жидкости превышает величину, равную одной атмосфере p = 1 кгс/см2 = 0,1 МПа. Эти приборы показывают долю давления сверх атмосферного. Для измерения в жидкости полного давления p необходимо к манометрическому давлению pман прибавить атмосферное давление pатм, снятое с барометра. Практически же в гидравлике атмосферное давление считается величиной постоянной pатм= =101325 100000 Па.
Пьезометр обычно
представляет собой вертикальную
стеклянную трубку, нижняя часть
которой сообщается с исследуемой
точкой в жидкости, где нужно измерить
давление (например, точка А на рис. 2),
а верхняя её часть открыта в атмосферу.
Высота столба жидкости в пьезометре
hp
является показанием этого прибора
и позволяет измерять избыточное
(манометрическое) давление в точке по
соотношению
, где hp — пьезометрический напор (высота), м. Упомянутые пьезометры применяются главным образом для лабораторных исследований. Их верхний предел измерения ограничен высотой до 5 м, однако их преимущество перед манометрами состоит в непосредственном измерении давления с помощью пьезометрической высоты столба жидкости без промежуточных передаточных механизмов. В качестве пьезометра может быть использован любой колодец, котлован, скважина с водой или даже любое измерение глубины воды в открытом резервуаре, так как оно даёт нам величину hp . Манометры чаще всего применяются механические, реже — жидкостные. Все манометры измеряют не полное давление, а избыточное . Преимуществами их перед пьезометрами являются более широкие пределы измерения, однако есть и |
1. История развития дисциплины. Труды Архимеда, Леонардо да-Винчи. Вклад в развитие науки Ньютона, Паскаля, Торичелли. Работы Ломоносова, Бернулли, Эйлера. Исследования Н.Жуковского. Наши современники и их вклад в развитие дисциплины.
Исторически сложилось так, что развитие гидромеханики, как у нас, так и за рубежом шло по двум направлениям:
☼ первый путь – теоретический, путь точного математического анализа, основанного на законах механики. Он привел к созданию теоретической гидромеханики, которая долгое время являлась самостоятельной дисциплиной не связанной с экспериментом. Однако на пути чисто теоретического исследования движения жидкости встречается много трудностей, и методы теоретической гидромеханики не всегда дают ответы на вопросы, выдвигаемые практикой.
☼ второй путь – путь широкого эксперимента и накопления опытных данных для использования их в инженерной практике – привёл к созданию технической гидромеханики или гидравлики. Этот путь возник из насущных задач практической инженерной деятельности людей. В начальный период своего развития гидравлика была наукой чисто электрической.
В настоящее же время в ней, где это возможно и целесообразно, всё больше применяют методы теоретической гидромеханики для решения отдельных задач, а теоретическая гидромеханика всё чаще начинает прибегать к эксперименту как к критерию достоверности своих выводов. Таким образом, различие в методах этих двух направлений одной и той же науки постепенно исчезает.
Из сказанного выше видно, что термины «Техническая гидромеханика», «Техническая механика жидкости» и «Гидравлика» следует рассматривать как имеющие одинаковое значение (как бы синонимы).
Гидравлика – очень древняя наука. За несколько тысяч лет до нашей эры в Индии, Китае, в Египте, странах Ближнего и Среднего востока уже строились различные гидротехнические сооружения: каналы, платины, водяные колеса. Методов расчета этих сооружений в то время не существовало и определенные достижения в гидротехническом строительстве были возможны благодаря искусству и практическому опыту строителей.
Первым научным трудом в области гидравлики считается написанный примерно за 250 лет до н.э. трактат Архимеда «О плавающих телах», в котором величайший ученый древности сформулировал закон о давлении жидкости на погруженное в нее тело.
Особое развитие гидравлика получила в средние века. В XVвеке Леонардо да Винчи написал труд «О движении и измерении воды в тесных сооружениях», опубликованный через 307 лет после его смерти в 1826 году.
В 1586 году голландский ученый Симон Стевин опубликовал работу «Начало гидростатики». В XVI – XVII веках Г. Галилей, Э. Торичелли, Б. Паскаль и И. Ньютон проводили исследования, позволившие разработать основы гидромеханики.
В 1755 – 1756 годах выходят в свет работы Л.П. Эйлера, где впервые приводится полная система дифференциальных уравнений равновесия и движения идеальной ж.
Основоположниками гидравлики как самостоятельной науки являются члены Петербургской академии наук М.В. Ломоносова, Д.И. Бернулли, Л.П. Эйлер. В 1738 году была опубликована работа Д. Бернулли «Гидравлика или записки о силах движения жидкости», в которой установлена зависимость между давлением и скоростью в элементарной струйке идеальной жидкости.
Представляют интерес такие работы Шизе, Вентури, Вейсбаха, Дарси, Базена и Рейнольдса. Труды этих ученых посвящены главным образом изучению турбулентности потоков и установлению общих законов сопротивления движению вязких жидкостей, а также исследованию движения жидкости в трубах, каналах и на водосливах. Большое внимание уделено в них также разработке теории размерности и подобия и постановке лабораторных экспериментов.
В 1791 году вышла в свет первое русское руководство по гидравлике А. Колмакова «Карманная книжка для вычисления количества воды, вытекающей через трубы, отверстие или по желобам, также и силы, какой они ударяют, стремясь с данной скоростью».
В конце XIX – начала XX века появились работы русских ученных: И.С. Громека, предположившего уравнения вихревого движения жидкости; Н.П. Петрова, разработавшего гидродинамическую теорию смазки; Н.Е. Жуковского, создавшего теорию гидравлического удара в трубах.
Большой вклад в развитие гидравлики принесли советские ученые: А.Н.Колмогоров (теория турбулентности), Н.Н Павловский (теория фильтрации, равномерное и неравномерное движение жидкости), И.Н. Куколевский (теория машиностроительной гидравлики), С.А.Христианович (неустановившиеся движения жидкости) и многое другие.
2. Понятие «жидкость». Капельная, реальная, идеальная, упругая жидкость. Силы, действующие в жидкости.
Жидкость легко подвижная среда, заполняющая объем без пустот и промежутков.
Жидкостью называют физическое тело, обладающее весьма большой подвижностью частиц, текучестью. Различают два вида жидкостей: капельные и газы. Капельные жидкости оказывают большое сопротивление изменению объема и трудно поддаются сжатию .(мало изменяют объем при изменении давления, легко принимают любую форму резервуара). Газы легко меняют объем при изменении давления и температуры, и имеют значительно меньшую плотность, чем капельные жидкости. В гидравлике различают жидкости реальные и идеальные. К идеальным относятся жидкости абсолютно не меняющие объем (несжимаемые), невязкие.(обладает текучестью, предложил Эйлер). Реальной жидкостью считается жидкость вязкая сжимаемая или несжимаемая.(обладает текучестью, вязкостью, сжимаемостью) В основном в гидравлике рассматриваются вязкие несжимаемые жидкости.
Упругая жидкость, которую называют жидкостью Максвелла (а также телом или моделью Максвелла). Эта жидкость не подчиняется закону вязкости Ньютона и поэтому называется неньютоновской жидкостью.
В гидравлике рассматривается два типа сил, действующих в жидкости: массовые и поверхностные.
Массовые силы обусловлены действующим на жидкость силовым полем, они приложены к каждой частице жидкости и пропорциональны их массе, примером таких сил являются силы тяжести(G=mg), силы инерции переносного движения (Fин=ma).
Поверхностные силы обусловлены взаимодействием рассматриваемого объема с окружающими его телами; силы реакции стенок сосуда; если рассматривается объем, мысленно выделенный из общей массы жидкости – это силы, действующие на него со стороны «отброшенной» жидкости, распределенные по поверхности объема и пропорциональны площади поверхности, на которую они действуют.(сила давления Р=РF/S, РF-поверхност. силы, S –площадь поверхности; сила трения τ= T/ω, T-касательная сила ,ω-площадь) Рпов=2σ/r; Pпов- напряжения в жидкости,σ - коэффициент поверхностного натяжения, r - радиус сферической поверхности, которую принимает жидкость. Δh=4σ/gdρ=k/d d – диаметр капилляра, k – коэффициент пропорциональности k=4σ/gρ
Под названием жидкость подразумевается одно из агрегатных состояний вещества. Жидкое состояние обычно считают промежуточным между твёрдым телом и газом: газ не сохраняет ни объём, ни форму, а твёрдое тело сохраняет и то, и другое. Вещество в жидком состоянии существует в определённом интервале температур, ниже которого переходит в твердое состояние (происходит кристаллизация либо превращение в твердотельное аморфное состояние — стекло), выше — в газообразное (происходит испарение). Границы этого интервала зависят от давления.В большинстве случаев жидкость является не только агрегатным состоянием, но и термодинамической фазой (жидкая фаза) квантовые жидкости и жидкие кристаллы.В технической гидромеханике под жидкостью понимают физическое тело, обладающее а) в отличие от твёрдого тела текучестью и б)в отличие от газа весьма малой изменяемостью своего объёма.
3. Механические характеристики жидкости. Физические свойства капельной жидкости (сжимаемость, вязкость, поверхностное натяжение, температурное расширение, капиллярность, испаряемость, растворимость газов.)
Плотностью -называется количество покоящейся массы данного вещества, заключенного в единице его объема. ρ=m/V (кг/м3) относительная плотность-соотношение плотности в-ва к плотности воды при -4 0 С
Удельный вес – вес единицы объема жидкости γ=G/V (H/ м3), γ=ρg; G вес жидкости в объеме V
Удельный объем – объем единицы массы покоящейся жидкости υ=1/ρ (м3/кг)
Текучесть - это легкоподвижность частиц жидкости, обусловловленная ее неспособностью воспринимать касательные напряжения в состоянии покоя. Поэтому жидкость не может сохранять собственную форму, а принимает форму сосуда (резервуара, водоема), в котором находится.
Сжимаемость - способность жидкостей уменьшать объем при увеличении давления. Характеризуется коэффициентом объемного сжатия βW, который представляет собой относительное изменение объема жидкости на единицу изменения давления: βW = - ΔV/VΔp,
гдеV - первоначальный объем жидкости; ΔV - приращение (изменение) этого объема при увеличении давления на величинуΔρ .Коэффициент объемного сжатия в системе СИ имеет размерность Па-1. Знак минус в этой формуле обусловлен тем, что положительному приращению давления ρ соответствует отрицательное приращение (т.е. уменьшение) объема жидкости.
Вязкость жидкостей - свойство жидкости сопротивляться относительному движению (сдвигу) ее частиц, обусловливающее появление силы внутреннего трения между слоями жидкости, если последние имеют различные скорости движения.( св-во обратное текучести). Это свойство характеризуется коэффициентами динамической μ и кинематической ν вязкостей. μ= τ/du*dy,
Где τ-сила, которая возникает на единице площади поверхности двух движущихся друг относительно друга слоев жидкости при градиенте скорости равный 1 (du -разность скоростей перемещающихся слоев воды, dy - толщина слоя). В международной системе единиц динамическая вязкость выражается в Н*с/м2 или Па*с
В практике для характеристики вязкости жидкости чаще применяют не коэффициент динамической вязкости, а коэффициент кинематической вязкости ν (м2/с или Стокс). 1 Ст=1 м2/с. Коэффициентом кинематической вязкости называется отношение коэффициента динамической вязкости к плотности жидкости: ν=μ/ρ,
Вязкость капельных жидкостей при увеличении температуры уменьшается, а вязкость газов возрастает
Сила поверхностного натяжения - это сила, обусловленная взаимным притяжением молекул жидкости, направленная по касательной к ее поверхности. Силы, действующие на поверхности раздела газ-жидкость, стремятся придать малому объему жидкости сферическую форму : Ep = Aвнеш = σS, Ep -потенциальной энергией, ΔAвнеш-работa внешних сил, S- площади поверхности, σ-коэффициент поверхностного натяжения(1 Н/м = 1 Дж/м2) σ= FH/2L
Δρ=2σ/r(для мыльного пузыря) Δρ-избыточное давление, σ-коэф. поверхностного натяжения, r-радиус; Δρ=4σ/r (капля жидкости)
Температурное расширение - способность жидкостей изменять объем при изменении температуры. Для капельных жидкостей характеризуется коэффициентом температурного расширения βT , равным относительному изменению объема при изменении температуры t на один градус при постоянном давлении: βT= ΔV/VΔt,
где V- первоначальный объем; ΔV- изменение этого объема при повышении температуры на величину Δt.Коэффициент температурного расширения в системе СИ имеет размерность град-1.Коэффициент зависит для данной жидкости от температуры и давления.
Капиллярными явлениями называют подъем или опускание жидкости в трубках малого диаметра – капиллярах. Смачивающие жидкости поднимаются по капиллярам, несмачивающие – опускаются. h=2σcosθ/ρgr
При полном смачивании θ = 0, cos θ = 1 h=2σ/ρgr=4σ/γd, θ-угол смачивания, ρ-плотность, γ-удельный вес,
Испаряемость жидкостей. При повышении температуры жидкости и, в некоторых случаях, при снижении давления часть массы капельной жидкости постепенно переходит в газообразное состояние (пар). Интенсивность процесса парообразования зависит от температуры кипения жидкости при нормальном атмосферном давлении: чем выше температура кипения жидкости, тем меньше её испаряемость. Однако, чем больше насыщенность паров при данной температуре, тем больше испаряемость жидкости.
Растворение газов - способность жидкости поглощать (растворять) газы, находящиеся в соприкосновении с ней. Все жидкости в той или иной степени поглощают и растворяют газы. Это свойство характеризуется коэффициентом растворимости kр. VГ/ Vж = kр P1 / P2 где VГ– объём растворённого газа при нормальных условиях, Vж– объём жидкости, P1 и P2– начальное и конечное давление газа.
Коэффициент растворимости зависит от типа жидкости, газа и температуры.

 акон
Паскаля
звучит так: внешнее давление, приложенное
к жидкости, находящейся в замкнутом
резервуаре, передаётся внутри жидкости
во все её точки без изменения. На этом
законе основано действие многих
гидравлических устройств:
гидродомкратов, гидропрессов,
гидропривода машин, тормозных
систем автомобилей.
акон
Паскаля
звучит так: внешнее давление, приложенное
к жидкости, находящейся в замкнутом
резервуаре, передаётся внутри жидкости
во все её точки без изменения. На этом
законе основано действие многих
гидравлических устройств:
гидродомкратов, гидропрессов,
гидропривода машин, тормозных
систем автомобилей.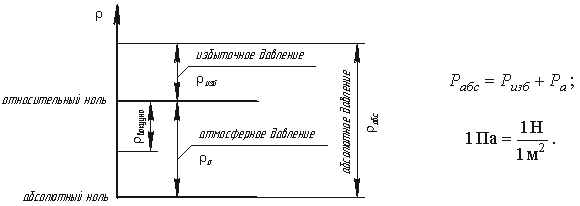 вакуумметр,
показывающий pв=0,04
МПа,
соответствует полному давлению
p=100000-40000=60000
Па, что
составляет 60 % от атмосферного.
вакуумметр,
показывающий pв=0,04
МПа,
соответствует полному давлению
p=100000-40000=60000
Па, что
составляет 60 % от атмосферного.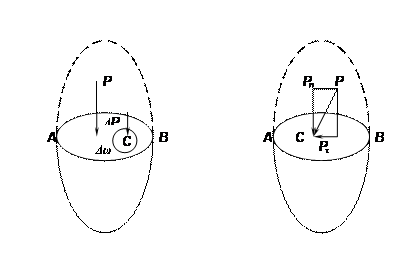 ервое
свойство.
Гидростатическое давление направлено
всегда по внутренней нормали к
поверхности, на которую оно действует.
ервое
свойство.
Гидростатическое давление направлено
всегда по внутренней нормали к
поверхности, на которую оно действует.
 торое
свойство
состоит в том, что в любой точке внутри
жидкости давление по всем направлениям
одинаково. Иначе на любую площадку
внутри объёма жидкости, независимо
от её угла наклона, действует одинаковое
давление.
торое
свойство
состоит в том, что в любой точке внутри
жидкости давление по всем направлениям
одинаково. Иначе на любую площадку
внутри объёма жидкости, независимо
от её угла наклона, действует одинаковое
давление.
