Содержание

1Определение структурной схемы 3

2Определение устойчивости системы 4

3Построение ЛАЧХ и ЛФЧХ линеаризованной не скорректированной системы 5

4Определение запасов устойчивости по фазе и амплитуде 6

5Построение ЛАЧХ скорректированной системы 7

6Определение ЛАЧХ корректирующего контура 9

7Выбор и расчет элементов корректирующего контура 10

8Уточнение структурной схемы и ЛАЧХ скорректированной системы 13

9Определение передаточной функции разомкнутой скорректированной системы автоматического управления 14

10Построение графика переходного процесса скорректированной системы 15

11Оценка точности системы АУ 17

Заключение 18

Список использованных источников 19

Приложение А. График ЛЧХ скорректированной, нескорректированной системыи КУ 20

Приложение Б. Вещественная характеристика и графики переходных процессов 20

1 Определение структурной схемы

Структурной схемой называется такая схема, в которой каждый математический операцией преобразование сигнала соответствует звену. Представим передаточную функцию как последовательность соединения звеньев: K= K₁ K₂ K₃ K₄

Структурная схема будет выглядеть следующим образом:

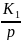
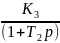
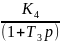
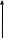
– интегрирующее

-

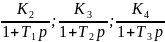2 Определение устойчивости системы.

Для определения устойчивости системы используем теорию Рауса-Гурвица. Для этого подставляем в передаточную функцию числовые значения.

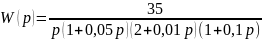
Преобразуем полученную функцию в характеристическое уравнение, т.е числитель и знаменатель складываем и приравниваем к 0.

35+p(1+0,05p)(1+0,01p)(1+0,1p)=0

35+p+0,05p²+0,01p²+0,05p²+0,05³(1+0,1p)=0

35+p+0,06p²+0,05p³+0,05p⁴=0

Это характеристическое уравнение четвертого порядка. Необходимым условием является положительность коэффициентов. Это условие соблюдается. Достаточным условием является положительность определителя третьего порядка.

Проверим достаточное условие, для чего составим матрицу:

Δ₃= > 0

Δ₃= (a₃x a₂ x a₄)+(a₄ x a₀ x 0)+(0 x a₄ x a₃)-(0 x a₂ x 0)-(a₃ x a₀ x a₃)-(a₁ x a₄ x a₄)<0

Δ₃=(0,05 x 0,06 x 0,05)-(0,05 x 35x 0,05)-(1 х 0,05 x 0,05)<0

Δ₃=-0,9<0

3 Построение ЛАЧХ И ЛФЧХ линеаризованной нескорректированной системы

Для построения ЛАЧХ и ЛФЧХ линеаризованной нескорректированной системы необходимо определить L(ω) и составить таблицу.

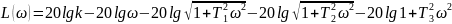
Φ(ω)= -90°-arctgT₁ω-arctgT₂ω-arctgT₃ω

Определим точку начала графика ЛАЧХ

20lgk=20lg x 35=30,8 Дб

Определяем частоты сопряжения для всех звеньев системы

ω_сопр1=1/T₁=20

ω_сопр2=1/T₂=100

ω_сопр3=1/T₃=10

Для построения ЛФЧХ необходимо выбрать значения ω, подставить в уравнение Φ(ω) и решить его, полученные результаты записать в таблицу.

ω,c-1	1	5	10	20
Φ(ω),°	-99,13	-133,39	-167,26	-209,73

Φ(ω)= -90°-arctgT₁ω-arctgT₂ω-arctgT₃ω

1) Φ(ω)= -90°-arctg0,05-arctg0.01-arctg0,1=-90°-2,86-0,57-5,7=-99,13

2) Φ(ω)= -90°-arctg0,05x5-arctg0.01x5-arctg0,1x5=-90°-14,03-2,86-26,5=-133,39

3) Φ(ω)= -90°-arctg0,05x10-arctg0.01x10-arctg0,1x10=-90°-26,56-5,7-45=-167,26

4) Φ(ω)= -90°-arctg0,05x20-arctg0.01x20-arctg0,1x20=-90°-45-11,3-63,43=-209,73

4 Определение запасов устойчивости по фазе и амплитуде

Исходя из полученного графика по критерию Найквиста, данная нескорректированная система неустойчива, т.к ЛАЧХ положительна при пересечении ЛФЧХ линии –π

Поэтому запасы устойчивости по фазе и амплитуде равны 0

Вывод: для нее необходима коррекция.

5 Построение лачх скорректированной системы

Для построения ЛАЧХ скорректированной системы необходимо определить W_ср.

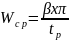
Исходя из этого, что допустимое перерегулирования: σ =30% по графику

β (σ ),опр.: β =30; t_p=0,9

По полученным данным определяем передаточную функцию скорректированной системы.

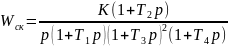
Определяем T:

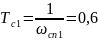ω’_сп1=1,6

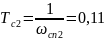ω’_сп2=8,5

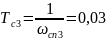ω’_сп3=26

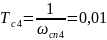ω’_сп4=100

Для заполнения таблицы необходимо выбрать значение ω, подставить в уравнение. Исходя из графика W(p)_ск определить запасы устойчивости по фазе и амплитуде.

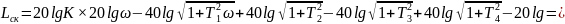
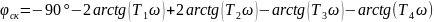
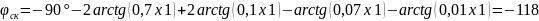
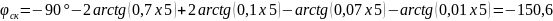
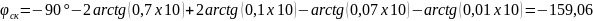
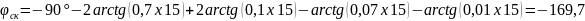
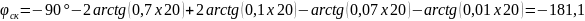
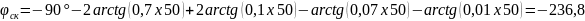
ω,c-1	1	5	10	15	20	50
(ω), °	-118	-150,6	-159.5	-169,7	-181,1	-236,8

Запас устойчивости определяется по графикам ЛАЧХ и ЛФЧХ скорректированной системы:

-запас устойчивости по фазе Δφ_ск=28°

-запас устойчивости по амплитуде Δl_ск=6Дб