Вариант 61

Задача 4

Для 10 магазинов , принадлежащих одному торговому предприятию, зафиксирована величина годового товарооборота У (млн.руб.) и величина торговой площади Х(тыс.м²).

Данные представлены в таблице:

хi	0,20	0,34	0,55	0,5	0,78	0,9	0,94	1,20	1,30	1,12
yi	20,06	38,00	41,00	41,83	56,56	68,00	75,31	89,00	91,15	91,50

На основе статистических данных, необходимо:

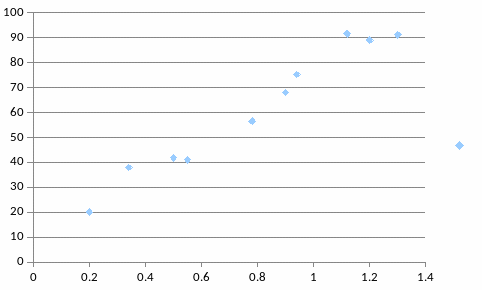
1. Построить корреляционное поле. Выдвинуть предположение о характере статистической зависимости между переменными X и Y .

2. Найти параметры линейного уравнения регрессии .

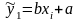Пояснить экономический смысл выборочного коэффициента регрессии.

3. Найти коэффициент парной корреляции и оценить тесноту связи на основе таблицы Чеддока.

4. Найти коэффициент детерминации R².

5. Оценить статистическую значимость уравнения регрессии на уровне 0,05, используя F-статистику.

6.Полученное уравнение регрессии изобразить графически.Сделать вывод окачестве построенной модели.

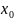7.Вычислить прогнозное значение при прогнозном значении , составляющем 130% от среднего уровня х.

Решение

1.Построим корреляционное поле.

Анализ рисунка позволяет сделать предположение о наличии линейной зависимости годового товарооборота У от величина торговой площади Х. При этом связь имеет положительную тенденцию, т.е. с увеличением величины торговой площади Х увеличивается годовой товарооборот У .

2. Найдём параметры линейного уравнения регрессии по формулам :

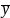b = ; a = - b∙

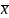
Рассчитаем сначала средние значения , , .

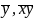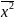№	y	x	x • y	y 2	x2
1	20.06	0.2	4.01	402.4	0.04
2	38	0.34	12.92	1444	0.12
3	41	0.55	22.55	1681	0.3
4	41.83	0.5	20.92	1749.75	0.25
5	56.56	0.78	44.12	3199.03	0.61
6	68	0.9	61.2	4624	0.81
7	75.31	0.94	70.79	5671.6	0.88
8	89	1.2	106.8	7921	1.44
9	91.15	1.3	118.5	8308.32	1.69
10	91.5	1.12	102.48	8372.25	1.25
Сумма	612.41	7.83	564.28	43373.35	7.39
Среднее	61,24	0,78	56,43	4337,34	0,74

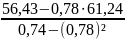
b = 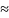67,33;

a = 61,24– 67,33∙ 0,78 8,72

Уравнения регрессии: 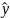= 67,33х + 8,72

Коэффициент регрессии b показывает, что при увеличении величины торговой площади на 1 тыс.м²., годовой товарооборот в среднем увеличивается на 67,33 млн.руб.

3.Найдём коэффициент парной корреляции по формуле :

=

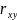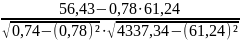= 0,984

Линейная связь между переменными Х и У прямая, и очень сильная.

4 . Коэффициент детерминации R²:

R² =

R² = (0,984)² 0,968

Таким образом ,изменение годового товарооборота У на 96,8% обусловлено изменением величины торговой площади Х и на 3,2% - действием неучтенных в модели факторов.

5. Оценим статистическую значимость уравнения регрессии , используя F-статистику с 95% надёжностью.

С помощью критерия Фишера проверяется нулевая гипотеза Hо о статистической незначимости уравнения регрессии. Конкурирующая гипотеза 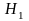– уравнение регрессии статистически значимо.

Наблюдаемое значение критерия Фишера вычислим по формуле:

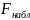= ∙ ( n -2),

= ∙ ( 10-2) =242

Найдём табличное значение критерия Фишера, 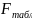определяется по таблицам

Для нашей задачи: ( ; ; 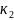α ),Степени свободы: =1, = n-2=10- 2=8, уровень значимости α =0,05

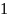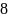( ; ; 0,05) =5,32.

Поскольку наблюдаемое значение 242 = > F_табл= 5,32, то нулевая

гипотеза Но о статистической незначимости уравнения регрессии отклоняется на уровне значимости α =0,05 и принимается конкурирующая гипотеза , т.е. признаётся статистическая значимость уравнения регрессии.

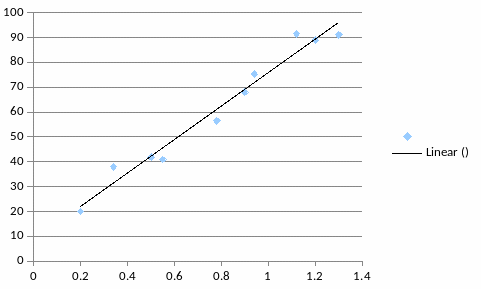
6.Построим линейное уравнение регрессии : = 67,33х + 8,72

Можно сделать вывод о правомочности применения линейной регрессионной модели. Полученное уравнение регрессии может быть использовано при прогнозировании.

7.Вычислим прогнозное значение при прогнозном значении , составляющем 130% от среднего уровня х:

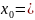1,3∙ = 1,3 ∙ 0,78 0,91 тыс.м²

. = 67,33∙ + 8,72

= 67,33∙ 0,91 + 8,72 69,99 (млн.руб.).