Решение транспортной задачи методом потенциалов

Идея метода заключается в вычислении для каждого пункта отправления и пункта назначения особых числовых показателей, названных потенциалами.

Каждой строке с номером i в матрице перевозок приписывается числовое значение , а каждому столбцу с номером j значение , называемых потенциалами, для каждой заполненной клетки (i; j ) выполняется условие: сумма потенциалов строки и столбца, в которых находится эта клетка, равна тарифу, соответствующему этой клетке:

Для незаполненных клеток сумма потенциалов ( ) не обязана совпадать с тарифом перевозки c_ij.

Ввиду этого тарифы c_ij можно назвать истинными тарифами перевозок, а суммы потенциалов косвенными тарифами.

Потенциалы и обозначают оплату за перевозку единицы груза в пунктах отправления (поставщиками) и назначения (потребителями) соответственно, поэтому их сумма равна транспортному тарифу .

Следовательно, алгебраическая сумма тарифов для свободной клетки равна разности ее истинного и косвенного тарифов: .

Так как занятых клеток на одну меньше, чем число потенциалов, то система (m+n-1) линейных уравнений с (m+n) неизвестными имеет бесчисленное множество решений. Среди них нам достаточно получить одно любое решение. Это можно достигнуть, полагая значение одного из потенциалов (все равно какого, например ) любым действительным числом (обычно полагают равным нулю, чтобы не усложнять вычисления остальных потенциалов).

Введем обозначение оценки свободной клетки .

Теорема (Достаточное условие оптимальности). Если для всех свободных клеток таблицы перевозок выполняется условие: ( ), то план оптимальный, причем, если ( ), для всех свободных клеток, оптимальный план единственный.

Если для некоторых пустых клеток ( ), то оптимальный план не единственный.

Если есть свободные клетки, для которых ( ), то рассматриваемый план перевозок не является оптимальным и может быть улучшен путем пересчета по циклу, соответствующему одной из клеток, в которых (лучше, если разность будет максимальной).

Таким образом, для вновь полученного плана поставок рассчитываем по занятым клеткам потенциалы, а затем оценки новых свободных клеток. Если критерий оптимальности выполняется для полученного плана, то задача решена. В противном случае продолжаем процесс перераспределения поставок до тех пор, пока не будет получено оптимальное решение транспортной задачи.

Проверим на оптимальность опорное решение предыдущей задачи методом потенциалов. Для этого составим систему потенциалов для заполненных клеток, выбран потенциал .

Система потенциалов имеет вид: Следовательно,

Полученные потенциалы _i для строк записываем в дополнительном столбце справа, а потенциалы столбцов _j в нижней дополнительной строке:

Поставщики	Потребители				Запасы поставщиков,
	B1	B2	B3	B4
A1	7 20	2 170	4 150	8 –	340
A2	8 –	9 –	6 –	5 200	200
A3	3 100	5 –	7 –	2 60	160
Спрос потребителей,	120	170	150	260

Рассчитаем косвенные тарифы и оценки свободных клеток таблицы поставок:

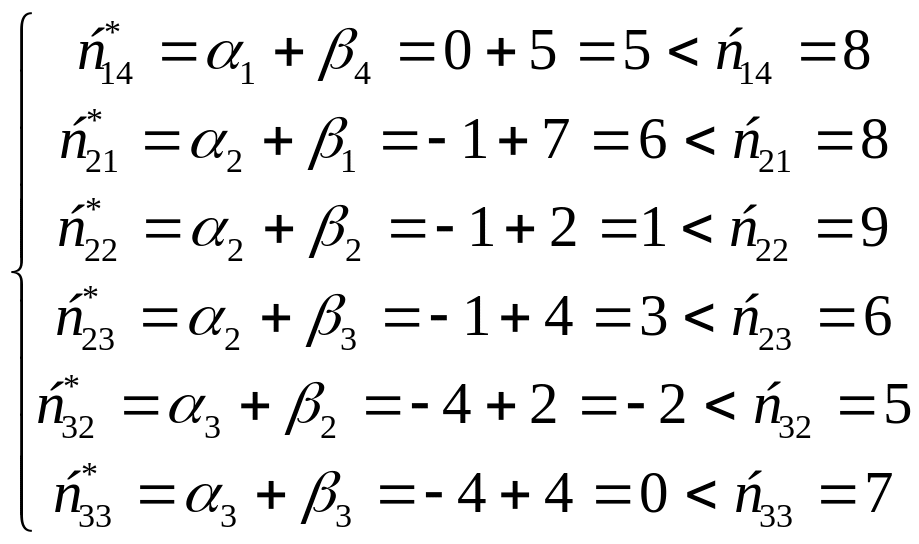
Поскольку все оценки свободных клеток положительны ( ), то найденный план является оптимальным и единственным планом транспортной задачи. Минимальная стоимость перевозок определяется значением целевой функции на этом плане, и она равна 2500 денежных единиц.

В результате получим опорный план

,

а значение целевой функции: Z = 2500ед.

Таким образом, преимущества метода потенциалов по сравнению с распределительным методом состоят в том, что отпадает необходимость построения циклов для каждой из пустых клеток и упрощается вычисление алгебраических сумм тарифов. Цикл строится только один – тот, по которому производится пересчет.

Применяя метод потенциалов, можно говорить не о знаке алгебраических сумм тарифов, а о сравнении косвенных тарифов с истинными. Требование неотрицательности алгебраических сумм тарифов заменяется условием, что косвенные тарифы не превосходят истинных.