Тема 6. Транспортная задача Постановка задачи

Транспортная задача (ТЗ) является одной из наиболее распространенных специальных задач линейного программирования.

Транспортным задачам присущи следующие особенности:

• распределению подлежат однородные ресурсы;

• условия задачи описываются только уравнениями;

• все переменные выражаются в одинаковых единицах измерения;

• во всех уравнениях коэффициенты при неизвестных равны единице;

• каждая неизвестная встречается только в двух уравнениях системы ограничений.

Стандартная транспортная задача состоит в определении оптимального плана перевозок некоторого однородного груза из m пунктов отправления (будем называть их поставщиками) в n пунктов назначения (потребители). При этом в качестве критерия оптимальности выбирают либо минимальную стоимость перевозок всего груза (план перевозок оптимален, если достигнут минимум затрат на его реализацию), либо минимальное время его доставки (план оптимален, если на его реализацию затрачивается минимум времени).

Рассмотрим экономико-математическую модель ТЗ, в которой критерием оптимальности взята минимальная стоимость перевозок всего груза.

Пусть в m пунктах отправления находится единиц однородного груза (запасы). Суммарный запас груза составляет . Кроме того, в n пунктах назначения подали заявку на поставку грузов в объемах единиц соответственно (потребности). Суммарная величина заявок потребителей составляет . Известны тарифы (транспортные издержки), связанные с доставкой единицы продукта из i-ого пункта отправления в j-ый пункт потребления. Общая стоимость перевозок составляет матрицу тарифов .

В общем виде исходные данные транспортной задачи представим в виде таблицы, которая называется транспортной или распределительной.

Строки транспортной таблицы соответствуют пунктам отправления, причем в последней клетке каждой строки указан объем запаса груза в i-м пункте .

Столбцы транспортной таблицы соответствуют пунктам назначения, причем последняя клетка каждого столбца содержит значение потребности j-го пункта потребления .

Поставщики	Потребители				Запасы поставщиков,
	B1	B2	…..	Bn
A1			…..		a1
A2			…..		a2
…..	…..	…..	…..	…..	…..
Am			…..		am
Спрос потребителей,	b1	b2	…..	bn

Все клетки таблицы (кроме тех, которые расположены в нижней строке и правом столбце) содержат информацию о перевозке из i-го пункта в j-й: в правом верхнем углу находится цена перевозки единицы продукта , а в левом нижнем — количество перевозимого груза для данных пунктов . Предполагается, что все .

Планом ТЗ называется матрица перевозок . Если в плане перевозок переменная принимает положительное значение ( ), то это будет записано в соответствующей клетке и она считается загруженной (занятой) или базисной; если же , то клетку называют свободной.

Составим экономико-математическую модель транспортной задачи.

Общие суммарные затраты, связанные с реализацией плана перевозок, можно представить целевой функцией .

Так как транспортные перевозки необходимо осуществить с минимальными транспортными издержками, то

Замечание. Вместо матрицы стоимостей перевозок (c_ij) можно задаваться матрицу расстояний, тогда в качестве целевой функции рассматривается минимум суммарной транспортной работы.

Переменные должны удовлетворять следующим условиям:

1. условие полного удовлетворения потребностей для всех пунктов потребления: .

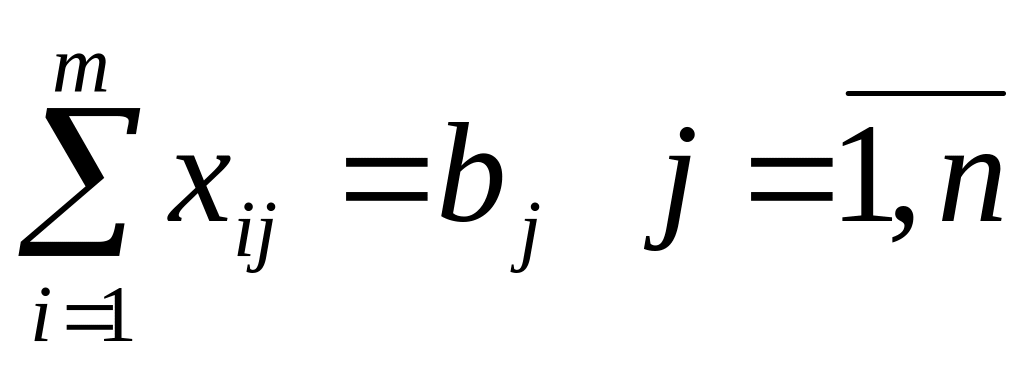2. весь продукт, хранимый на всех пунктах отправления, должен быть вывезен: .

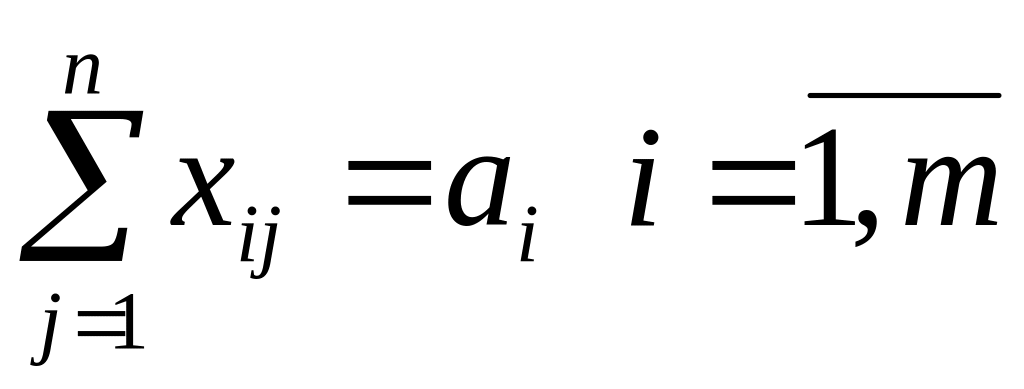3. все .

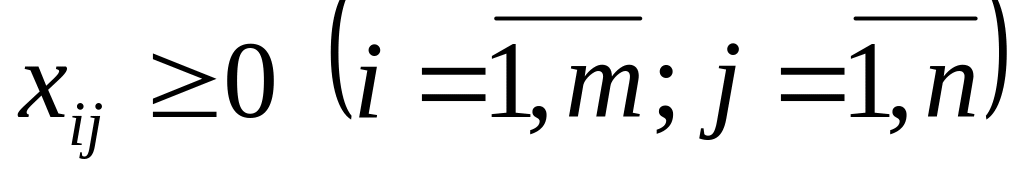Таким образом, экономико-математическая модель транспортной задачи имеет следующий вид:

.

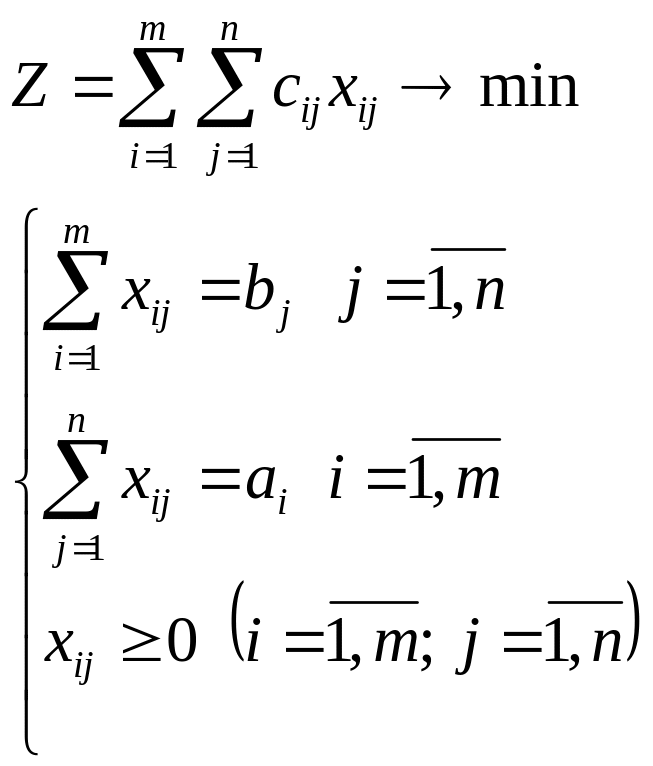Опорный план является допустимым решением транспортной задачи и используется в качестве начального базисного решения при нахождении оптимального решения.

План , при котором функция принимает минимальное значение, называется оптимальным.

Таким образом, решить транспортную задачу − значит на множестве неотрицательных решений системы ограничений найти такое решение, при котором линейная функция принимает минимальное значение.

Транспортная задача называется закрытой (сбалансированной), если суммарный объем запасов равен суммарному объему потребления:

.

Если такого равенства нет (потребности выше запасов или наоборот), задачу называют открытой, т.е.: .

Теорема (Критерий разрешимости транспортной задачи). Транспортная задача разрешима тогда и только тогда, когда она является сбалансированной, т.е.

.

Если в исходных условиях дана открытая задача, то ее необходимо привести к закрытой форме, для чего следует произвести следующее:

а) случай дефицита (суммарное потребление строго больше суммарных запасов ). В этом случае вводят фиктивный пункт отправления с запасами, равными с нулевыми тарифами перевозок во все пункты отправления (вводим фиктивную базу, из которой вывоз осуществляется по нулевым тарифам)

б) случай избытка продукта (суммарные запасы строго больше суммарного потребления ). В этом случае вводят фиктивный пункт потребления с объемом потребностей , перевозки в который из всех пунктов отправления осуществляется с нулевыми тарифами.

Рассмотрим ограничения задачи. Общее число уравнений в ограничениях равно m+n, а число переменных равно . Так как присутствует условие сбалансированности задачи , которое «связывает» некоторые из этих m+n уравнений, то число линейно независимых уравнений равно m+n-1. Следовательно, любое опорное решение должно содержать не более m+n-1 отличных от нуля переменных.

Если в опорном плане число положительных компонент в точности ровно m+n-1 (остальные нулевые), то план невырожденный.

Если в опорном плане число положительных компонент строго меньше m+n-1, то план вырожденный.

Для исключения вырожденности задачи целесообразно ввести в свободную клетку (клетки, если их несколько) с наименьшим тарифом нулевую поставку, причем его помещают в такую клетку, чтобы в каждой строке и каждом столбце было не менее одной занятой клетки. Необходимо также тщательно подходить к выбору клетки, в которую заносится 0, что бы в последующем она не попала в клетки цикла пересчета, имеющие отрицательное значение, так как из нуля нельзя производить вычитание, поэтому его надо записывать в клетку, которая соответствует положительным значениям в циклах пересчета.

Особенности системы ограничений ТЗ.

1. Коэффициенты при неизвестных во всех ограничениях равны единице.

2. Любая переменная встречается только в двух уравнениях.

3. Система ограничений содержит m+n уравнений с переменными.

4. Любое опорное решение должно содержать m+n-1 базисных переменных и 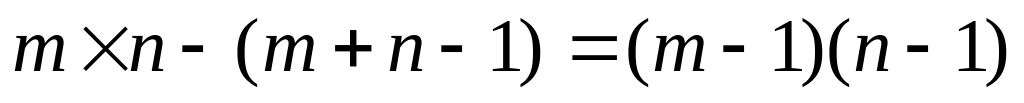свободных переменных, равных нулю.

5. Если все и – целые, тогда значения базисных переменных в допустимом базисном решении тоже целые.

Рассмотрим экономико-математическую модель транспортной задачи на следующем примере.

Пример. Имеются три поставщика некоторого товара и четыре потребителя этого товара. Причем известна стоимость перевозки товара от каждого поставщика к каждому потребителю. Требуется найти объемы перевозок для каждой пары «поставщик − потребитель» так, чтобы суммарные затраты на перевозку были минимальны, запасы всех поставщиков реализованы и потребности всех потребителей удовлетворены.

Обозначим через x_ij объем поставляемого товара от i -го поставщика к j- му потребителю.

Поставщики	Потребители				Запасы поставщиков,
	B1	B2	B3	B4
A1	7	2	4	8	340
A2	8	9	6	5	200
A3	3	5	7	2	160
Спрос потребителей,	120	170	150	260

Чтобы запасы каждого поставщика были полностью реализованы, должны быть справедливы уравнения баланса для каждой строки таблицы поставок, т. е. выполняться равенства

Чтобы спрос каждого из потребителей был удовлетворен, должны быть справедливы уравнения баланса для каждого столбца таблицы поставок, т.е.

Поскольку объем перевозимого груза величина неотрицательная, то должны выполняться ограничения на переменные x_ij: .

Суммарные затраты Z на перевозку определяются указанными в таблице поставок тарифами перевозок и размерами поставок:

Таким образом, экономико-математическую модель транспортной задачи экономико-математическую модель транспортной задачи имеет вид:

Так как ТЗ является задачей ЛП, то ее можно решить с помощью симплексного метода. Однако в силу специфики системы ограничений (каждое неизвестное входит лишь в два уравнения системы и коэффициенты при неизвестных равны единице) были разработаны специальные методы определения первоначального опорного плана и специальное представление структуры данных задачи, которые позволили решать задачу более простыми (по сравнению с таблицами) средствами. Эти методы, как и симплексный метод, позволяют найти начальное опорное решение, а затем, улучшая его, получить оптимальное решение.