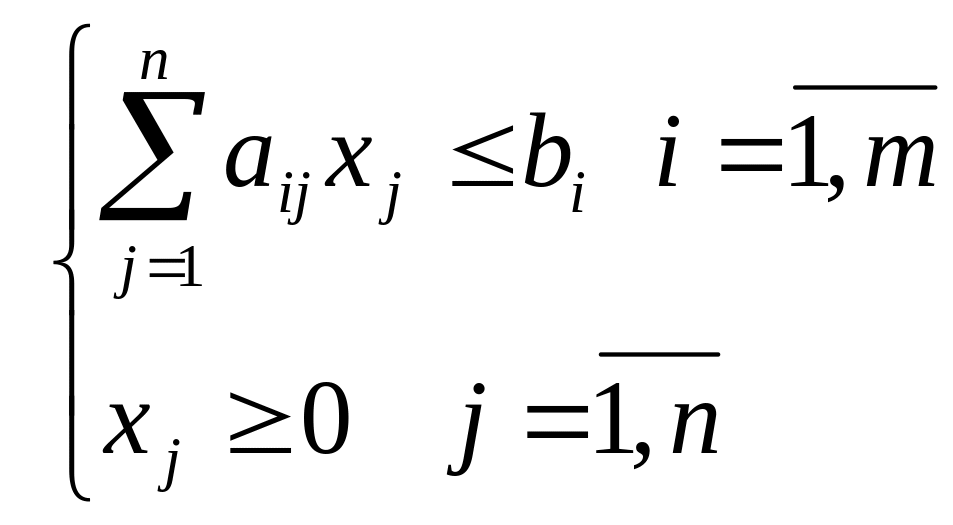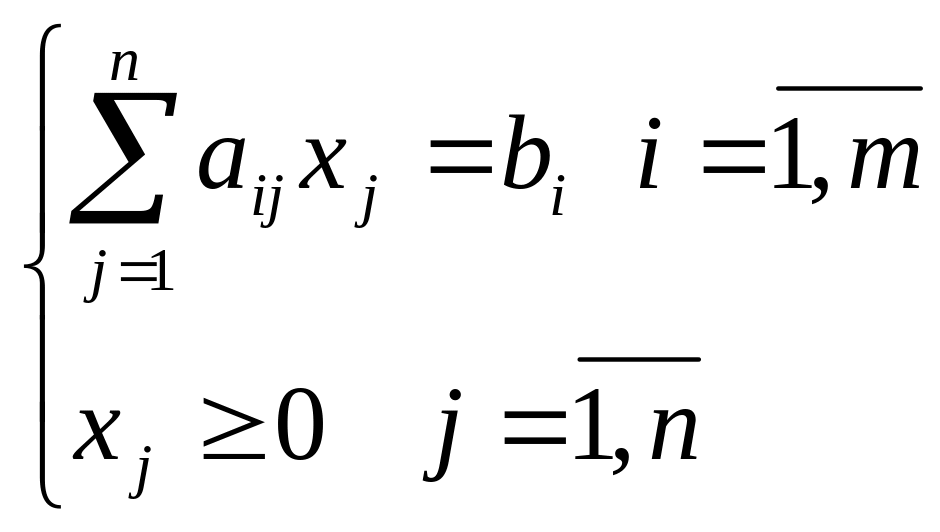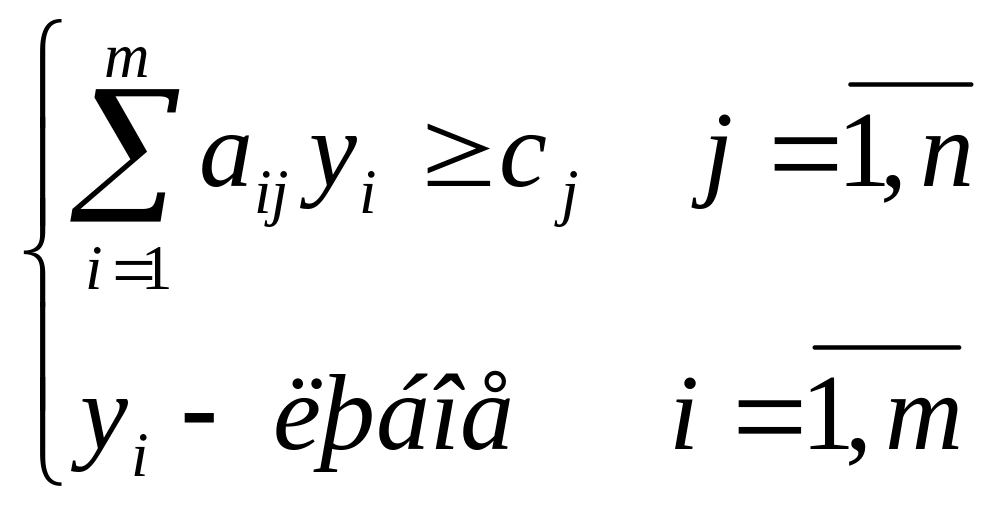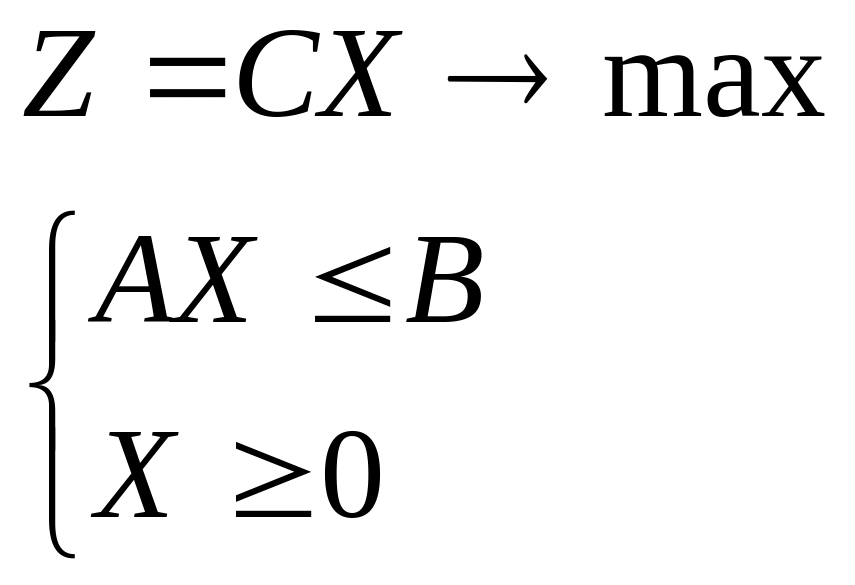Тема 4. Двойственные задачи линейного программирования Прямая и двойственная задачи.

Важную роль в линейном программировании играют двойственные или сопряженные задачи, особенно по отношению к задачам, связанным с планированием производства и распределением ресурсов.

Идея двойственности заключается в том, что нельзя получить максимальную прибыль не минимизировав затраты.

Каждой задаче линейного программирования можно определенным образом поставить в соответствие другую задачу линейного программирования, называемую сопряженной или двойственной по отношению к исходной или прямой задаче, сформулированную по стандартным правилам.

Каждая из этих задач может быть решена самостоятельно, но при этом допустимые решения их прямо связаны между собой, что позволяет, зная оптимальное решение одно из них, определить оптимальное решение другое, при этом часто решение двойственной задачи намного легче найти, чем решение прямой.

В качестве примера рассмотрим задачу планирования производства.

Задача: Предприятие № 1 имеет m видов ресурсов в количестве b_i (i= ) единиц каждого вида ресурсов, из которых производится n – видов продукции. Для производства единицы j-ого вида продукции используется a_ij-единиц i-того вида ресурсов, а стоимость единицы продукции c_j. Необходимо составить план выпуска продукции (указать, сколько и какого типа надо произвести) обеспечивающей ее максимальную стоимость.

Это прямая задача. Следовательно, прямая задача линейного программирования в стандартной форме звучит следующим образом: надо определить вектор , удовлетворяющий ограничениям

и обеспечивающей максимум целевой функции .

Допустим, что предприятие № 2 решило закупить все ресурсы, которыми располагает предприятие № 1. В этом случае предприятию № 2 необходимо установить оптимальные цены на эти ресурсы.

Поставим каждому ограничению исходной задачи в соответствие двойственную переменную как вектор оценок видов сырья, где y_i - оценка стоимости единицы i-того ресурса.

Оценка ресурсов исходит из следующих условий:

• Общая стоимость ресурсов (общие затраты) для предприятия № 2 должна быть минимальной: ;

• Стоимость всех ресурсов, затраченных на продажу единицы j-го товара, должна быть не меньше дохода, получаемого при реализации единицы j-го товара (за каждый вид ресурса предприятию № 1 надо уплатить не менее той суммы, которую это предприятие могло бы получить при переработке данного вида ресурса в готовую продукцию, т.е. не меньше стоимости окончательного продукта): .

Таким образом, двойственная задача по отношению к исходной задаче планирования производства формально записывается следующим образом: необходимо определить вектор , обеспечивающий минимум функции

при ограничениях

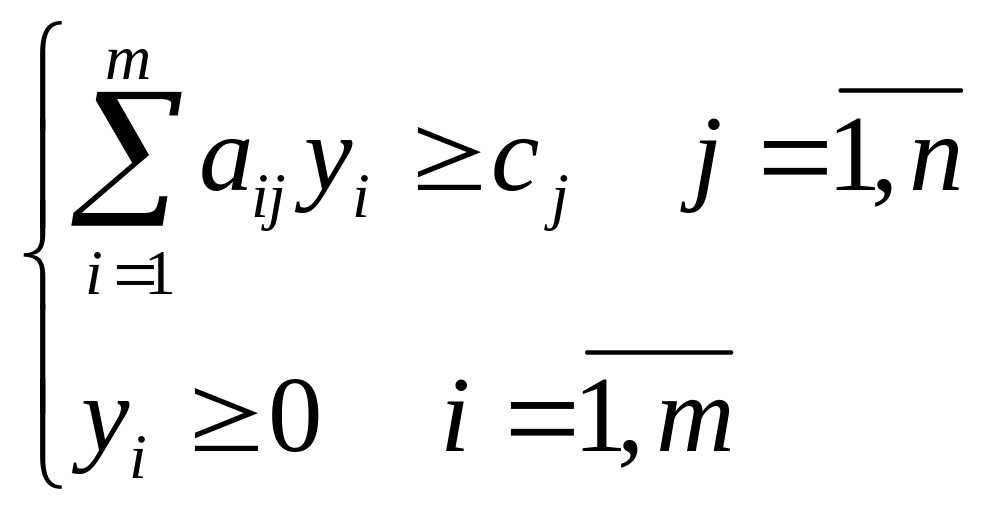
Замечание. Стоимостное выражение ресурса не есть его цена, т.е. – это неявные или учетные цены.

Экономически двойственные задачи можно интерпретировать следующим образом.

Прямая задача: сколько и какой продукции необходимо произвести, чтобы при заданных стоимостях единицы продукции , объемах имеющихся ресурсов и нормах расходов получить максимальную прибыль от реализации произведенной продукции?

Двойственная задача: какова должны быть оценка единицы каждого из ресурсов , чтобы при заданных количествах ресурсов , величинах стоимости единицы продукции и нормах расходов общие затраты производства были минимальными?

Прямая и двойственная задачи образуют пару задач, называемую в линейном программировании двойственной парой.

Двойственные задачи обычно подразделяют на симметричные и несимметричные.

Двойственные задачи, ограничения которых задаются неравенствами, называются симметричными, одна из которых называется основной, а другая - двойственной.

Таким образом, пара симметричных двойственных задач имеет вид:

Прямая задача	Двойственная задача

Двойственные задачи, ограничения которых задаются уравнениями, называются несимметричными. Это означает, что в несимметричном случае двойственная переменная свободна по знаку.

Несимметричные двойственные задачи имеют вид:

Прямая задача	Двойственная задача

Введем обозначения:

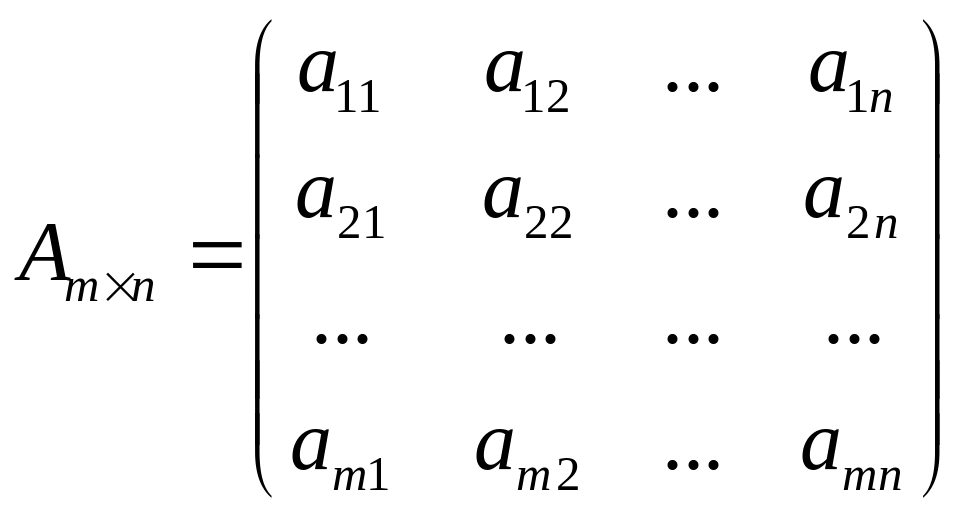• – матрица коэффициентов системы ограничений;

• – матрица-строка коэффициентов целевой функции;

• – матрица-столбец свободных членов;

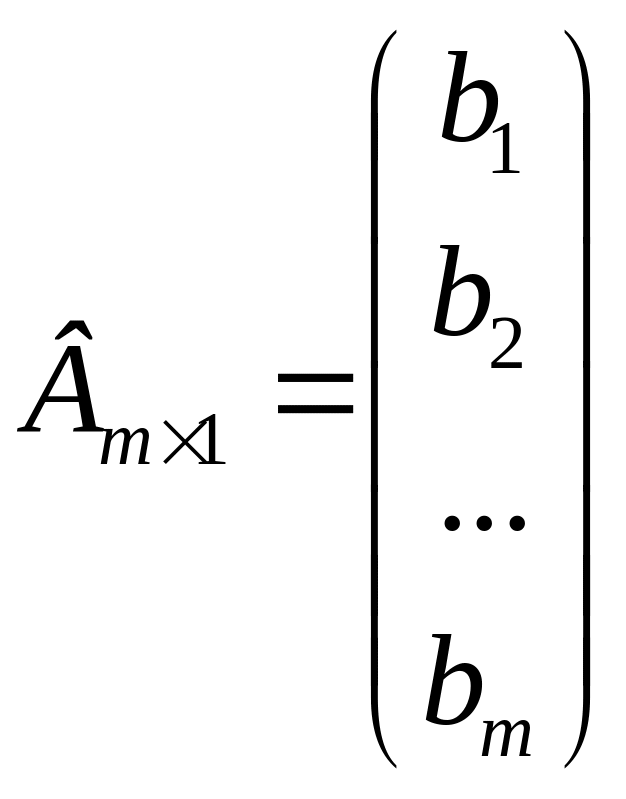• – матрица-столбец неизвестных.

Тогда схема составления двойственных задач имеет вид:

Схема составления двойственных задач

Прямая задача	Двойственная задача

Сравнивая две сформулированные задачи, видно, что двойственная задача составляется согласно следующим правилам.

1. Если целевая функция задачи исследуется на max, то ограничения должны иметь знак « » или «=», а если целевая функция задачи исследуется на min, то ограничения должны иметь знак « » или «=».

2. Каждому ограничению исходной задачи ставится в соответствие двойственная переменная , и наоборот, т.е. число переменных двойственной задачи равно числу ограничений прямой задачи, а число ограничений двойственной задачи равно числу переменных исходной задачи.

3. Если целевая функция прямой задачи исследуется на max, то целевая функция двойственной задачи исследуется на min, и наоборот: .

4. Коэффициенты целевой функции прямой задачи являются свободными членами системы ограничений двойственной задачи.

5. Свободные члены системы ограничений прямой задачи 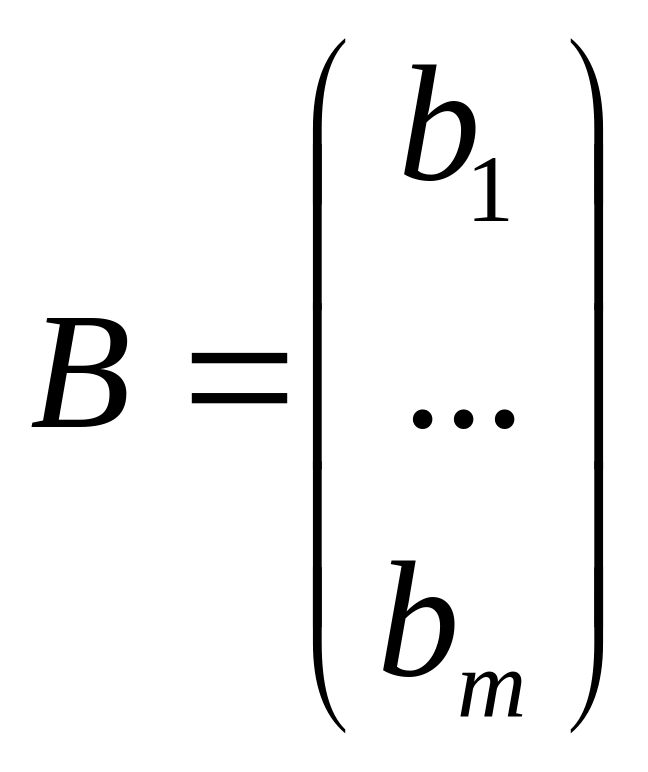являются свободными коэффициентами целевой функции двойственной.

6. Матрица коэффициентов системы ограничений прямой и двойственной задач являются транспонированными друг к другу.

7. Если на переменную прямой задачи наложено ограничение на знак (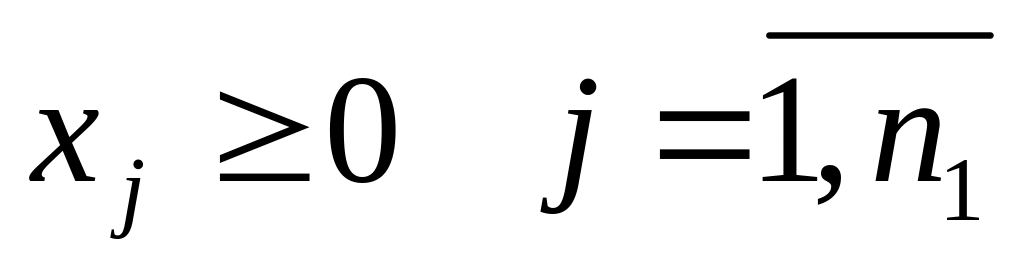 ), то j-е ограничение двойственной задачи записывается в виде неравенства, и наоборот.

8. Если переменная 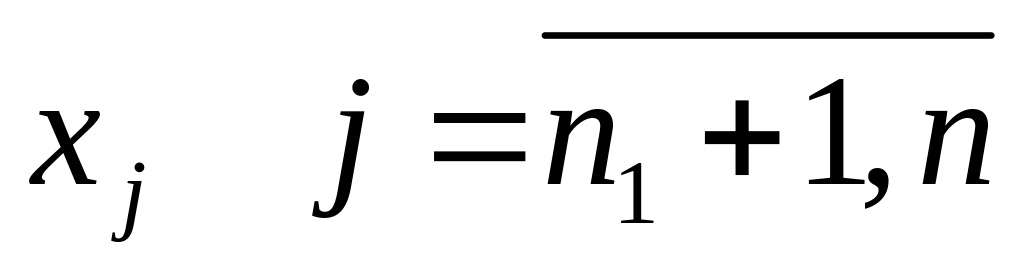исходной задачи произвольная по знаку, то j-е ограничение двойственной задачи имеет вид равенства, и наоборот.

9. Если в прямой задаче имеются ограничения-равенства, то на соответствующие переменные двойственной задачи не налагаются условия неотрицательности.

10. Если на переменную двойственной задачи наложено условие неотрицательности , то в прямой задаче соответствующее ограничение двойственной задачи записывается в виде неравенства.

Задача. Составить к следующей задаче ЛП двойственную:

Решение.

1. Упорядочим запись задачи. Для этого первое ограничение умножим на (-1):

2. Каждому ограничению исходной задачи поставим в соответствие двойственную переменную

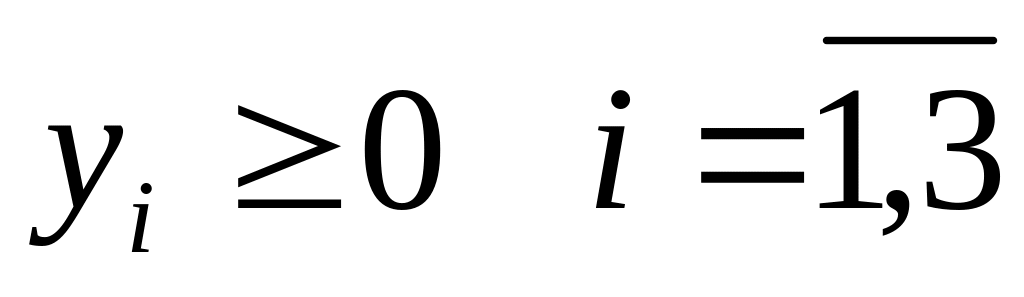
Таким образом, число переменных исходной задачи равно числу ограничений двойственной, т.е. m=3.

3. Так как целевая функция прямой задачи исследуется на max, то целевая функция двойственной задачи будет исследоваться на min:

4. Свободные члены системы ограничений прямой задачи 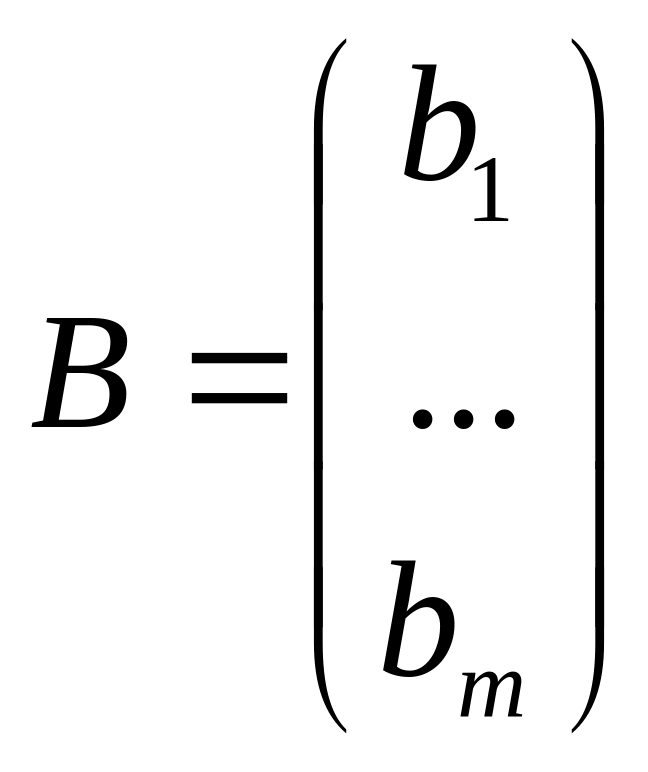станут свободными коэффициентами целевой функции двойственной, т.е.

5. Коэффициенты целевой функции прямой задачи станут свободными членами системы ограничений двойственной.

6. Матрица коэффициентов системы ограничений прямой и двойственной задач являются транспонированными друг к другу, т.е.

7. Так как все три переменные исходной задачи принимают только лишь неотрицательные значения, то в системе ограничений двойственной задачи должны быть три неравенства. Вид неравенства выбирается по целевой функции. Поскольку F исследуется на min, то неравенства должны быть со знаком «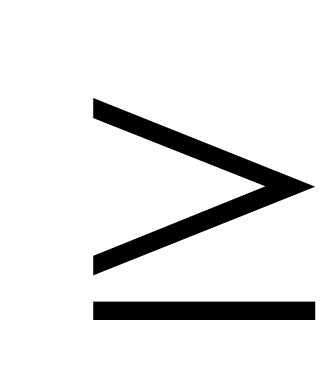 ». Следовательно, система ограничений примет следующий вид:

8. Так как второе ограничение в прямой задаче имеются вид равенства, то на соответствующую переменную двойственной задачи не будет налагаться условие неотрицательности .

Таким образом, двойственная задача имеет вид:

при ограничениях