22

Содержание

1. Первообразная функция и неопределенный интеграл

2. Таблица простейших интегралов

3. Интегрирование методом замены переменной

4. Метод интегрирования по частям

5. Понятие о неберущихся в конечном виде интегралах

6. Интегрирование рациональных функций

7. Интегрирование тригонометрических рациональных выражений

8. Интегрирование простейших иррациональных выражений

Н Е О П Р Е Д Е Л Ё Н Н Ы Й И Н Т Е Г Р А Л

1. Первообразная функция и неопределенный интеграл

Восстановление функции F(x) по известной производной этой функции F'(x)=f (x) (или по известному ее дифференциалу dF(x)=f(x)dx) называется интегрированием, а искомая функция F(x) называется первообразной функцией.

Всякая функция f(x) имеет бесчисленное множество различных первообразных функций, отличающихся друг от друга на постоянное слагаемое, т.е. если F(x) – первообразная для f(x), то и F(x)+C, где С - произвольная постоянная, есть также первообразная для f(x), действительно

[F(x)+C]'=F'(x)=f(x). Cовокупность всех первообразных F(x)+C одной и той же функции f(x) называется неопределенным интегралом этой функции и обозначается символом

, (1)

где x - переменная интегрирования, f(x) - подынтегральная функция, f(x)dx - подынтегральное выражение.

Геометрически, графики всех первообразных функций для f(x) представляют в системе координат XOY семейство кривых, которые получаются одна из другой путем параллельного переноса вдоль оси Y на величину С.

Как следует из понятия неопределенного интеграла, интегрирование и нахождение дифференциала являются обратными действиями. Действительно, если первообразная, а значит и неопределенный интеграл для функции f(x) существует, то подынтегральное выражение представляет собой дифференциал любой из этих первообразных

f(x)dx=F'(x)d(x)=dF(x),

тогда

d∫f(x)dx=d[F(x)+C]=F'(x)dx=f(x)dx, (2)

∫dF(x)=∫ f(x)dx=F(x)+C, (3)

т.е. знаки d и ∫ взаимно сокращаются.

Укажем основные свойства неопределенного интеграла, правильность которых можно проверять дифференцированием.

І. Постоянный множитель выносится за знак интеграла.

∫Af(x)dx=A∫ f(x)dx (4)

2. Интеграл от алгебраической суммы (разности) функций равен сумме (разности) интегралов.

∫[f(x)± φ(x)]dx=∫f(x)dx ±∫φ(x)dx . (5)

3. Неопределенный интеграл не зависит от выбора переменной интегрирования.

∫f(u)du= F(u)+C, (6)

где u - независимая переменная или функция x, u=u(x). Этот результат следует непосредственно из правила дифференцирования сложной функции

; , ,

тогда

.

4. Интеграл ∫udv может быть сведен к интегралу ∫vdu.

Из формулы дифференцирования произведения двух функций d(uv)=udv+vdu

интегрированием получается следующее равенство

∫udv = uv – ∫vdu, (7)

которое называется формулой интегрирования по частям.

2. Таблица простейших интегралов

Пользуясь тем, что интегрирование – операция обратная вычислению дифференциала можно записать основные формулы интегрирования

1. α ≠ -1

2.

3.

4.

5.

6.

7.

8.

9.

Для полноты таблицы добавим еще две формулы.

10.

11.

В этих формулах u - независимая переменная или функция от независимой переменной, a – постоянная (в формуле 7 а ).

Приведем простейшие примеры вычисления интегралов:

Пример 1.

Пример 2.

Пример 3.

1.Разлагая интеграл 1 по свойству 2 на три интеграла и вынося постоянный множитель за знак интеграла (свойство 1), приведем интеграл к следующему виду:

далее первый и второй интегралы вычисляются по формуле 1 таблицы, а

в третьем - знаки ∫ и d взаимно сокращаются (интегрирование и взятие дифференциала – обратные действия).

.

2.Интеграл табличный, формула 3.

3.Подынтегральная функция (пр.3) может быть преобразована и сведена к разности двух функций, а значит к двум интегралам, интегрируемых по формуле 1 таблицы.

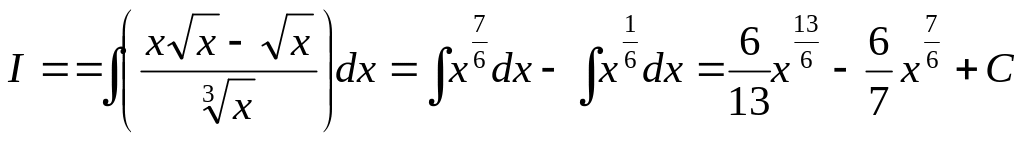
Для вычисления различных интегралов дополним таблицу определенными приёмами и методами интегрирования.