2.2 Свойства определителей

Для определителей справедливы следующие утверждения, называемые свойствами определителей.

1. Определитель не изменяется при транспонировании: detA^T=detA.

2. Если строка (столбец) матрицы A равна линейной комбинации соответственных строк (столбцов) матриц A и B, а остальные строки (столбцы) этих матриц совпадают, то ее определитель равен линейной комбинации определителей матриц A и B:

A_i = a·B_i + b·C_i, detA = a·detB + b·detC,

A^(j) = a·B^(j) + b·C^(j), detA = a·detB + b·detC .

3. При перестанровке любых двух строк (столбцов), определитель меняет знак.

4. Если в определителе есть две одинаковые строки (два одинаковых столбца), то он равен нулю.

5. Если в определителе есть две пропорциональные строки (два пропорциональные столбца), то он равен нулю.

6. Определитель не изменится, если к элементам любой его строки (столбца) прибавить элементы любой другой строки (столбца), умноженные на одно и то же число.

7. Определитель, содержащий нулевую строку (нулевой столбец), равен нулю.

8. Сумма произведений элементов любой строки (столбца) на алгебраические дополнения другой строки (другого столбца) равна нулю.

9. Определитель произведения матриц равен произведению определителей сомножителей.

Перечисленные свойства позволяют упростить вычисление определителя.

Пример. 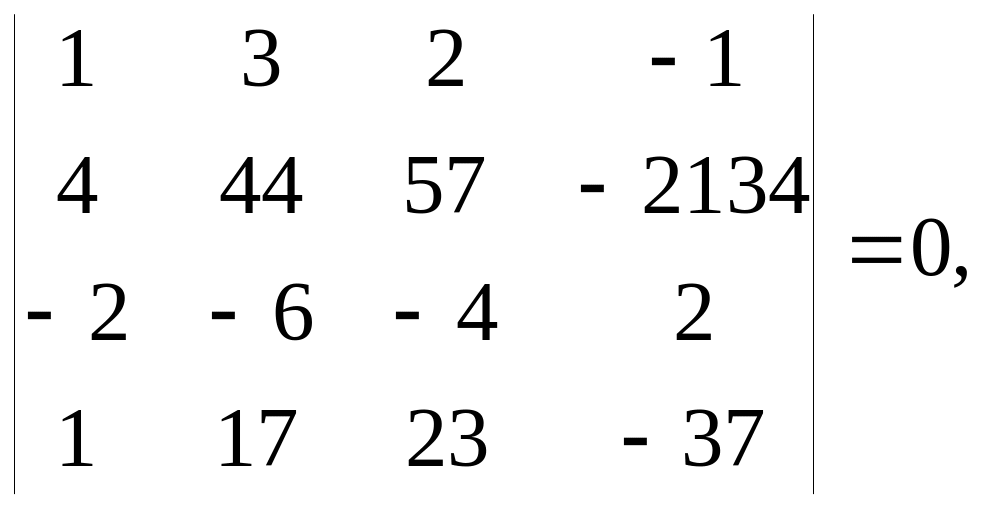поскольку 1-я и 3-я строки пропорциональны.

9.2 Виды матриц. Ранг матрицы

Любая таблица, состоящая из чисел, записанных в определенном порядке, содержащая m строк и n столбцов, называется матрицей размерности m×n; число a_ij – элемент матрицы.

Способы задания матриц:

А_1×n – матрица-строка

А_1×m – матрица-столбец

Матрица, все элементы которой – нули – нулевая матрица.

Если m≠n, матрица – прямоугольная;

если m>n, матрица – укороченная;

если m<n, матрица – удлиненная;

если m=n, матрица – квадратная.

|A| – определитель матрицы.

Размерность квадратной матрицы называется ее порядком.

Если определитель квадратной матрицы ≠ 0, то такая матрица – невырожденная (неособенная);

Если определитель квадратной матрицы = 0, то такая матрица – вырожденная (особенная).

Квадратная матрица вида

где а₁₁, а₂₂, … , а_nn – элементы , распределенные по главной диагонали, называется диагональной матрицей.

Диагональная матрица, все элементы которой по главной диагонали равны 1, называется единичной матрицей (E_n).

Любое число можно считать матрицей первого порядка.

Если у матрицы переставить местами столбцы со строками, то такая операция называется транспонированием матрицы.

А^т – транспонированная матрица.

|А| = |А^т| (если А – квадратная)

(А^т)^т = А

Квадратная матрица называется симметрической, если А = А^т , т.е. a_ij = a_ji для любых i и j.

Элементы симметрической матрицы, расположенные симметрично относительно главной диагонали, равны.

Квадратная матрица называется ортогональной, если ее столбцы образуют ортонормированную систему векторов.

Рассмотрим матрицу А = (a_ij), i = 1, m ; j = 1, n.

Из этой матрицы можно образовать квадратные матрицы. Определители таких матриц называют минорами данной матрицы. Порядок этих миноров не превышает min(m, n).

Пример:

Для матрицы А_5×4 наибольший порядок минора ≤ 4.

– квадратная матрица 3 порядка:

9 миноров 1 порядка;

9 миноров 2 порядка;

1 минор 3 порядка;

Рангом матрицы называется максимальный порядок миноров матрицы, отличных от нуля.

Если ранг матрицы r(A) = r, то по крайней мере один из миноров этой матрицы порядка r отличен от нуля, и все миноры более высоки порядков (если они существуют) равны 0.

Ранг матрицы можно вычислить следующими методами:

1) Метод окаймляющих миноров

2) Метод, основанный на элементарных преобразованиях матрицы

Рассмотрим первый метод.

r(A) может принимать значения 1, 2, 3.

Выбираем минор первого порядка:

М₁ = -3

Составляем М₂, окаймляющий М₁ ≠ 0

= 21 ≠ 0

=> r(A) = 2 или 3.

Составляем М₃, окаймляющий М₂ ≠ 0

≠ 0

=> r(A) = 3

Базисным минором матрицы называется минор, не равный нулю, порядок которого равен рангу данной матрицы.

называется трапецеидальной.

Каждую матрицу с помощью элементарных преобразований можно превратить в трапецеидальную. Ранг трапецеидальной матрицы равен числу ненулевых строк.

Т.к. элементарные преобразования матрицы не меняют ее ранга, то для отыскания ранга любой матрицы нужно:

1) Преобразовать данную матрицу в трапецеидальную;

2) Подсчитать число ненулевых строк

3) Ранг трапецеидальной матрицы будет равен рангу данной матрицы.