Лабораторная работа№2 Исследование эквивалентности непрерывного и цифровых звеньев сар 2.1. Принципы цифрового управления непрерывными объектами

• 2.2. Типовая ветвь АИСАР. Математическое описание

• 2.3. Задания к работе

Цифровое управление (управление с помощью компьютера, цифрового процессора) непрерывным во времени объектом требует преобразования непрерывных сигналов во временную последовательность чисел, представленных в двоичном коде, выполнения математических операций над этой последовательностью в соответствии с алгоритмом управления, и обратного преобразования полученного результата в непрерывный во времени сигнал. Этот сигнал подается на исполнительный механизм и далее, через регулирующий орган, воздействует на объект управления. Такого рода гибридные системы (системы, состоящие из блоков, работающих в дискретном и непрерывном времени) имеют свои характерные особенности и требуют для своего описания специального математического аппарата.

2.1. Принципы цифрового управления непрерывными объектами

• 2.1.1. Функциональные схемы САР с аналоговыми и цифровыми регуляторами

• 2.1.2. Квантование и дискретизация сигналов

2.1.1. Функциональные схемы сар с аналоговыми и цифровыми регуляторами

Технические и физические объекты управления и устройства управления ими (исполнительные механизмы и регулирующие органы) как правило, являются непрерывными во времени. Здесь имеется в виду то, что выходные величины этих устройств являются непрерывными функциями времени. Достаточно долгое время и регуляторы САР строились как непрерывные, в виде физических схем. Начиная с 70 гг. 20 века, с широким внедрением цифровой компьютерной техники появилась возможность реализации алгоритмов регулирования (например, ПИ, ПИД и др.) в цифровом виде.

Отметим два основных достоинства цифровой реализации алгоритмов управления:

• - простота изменения алгоритма управления (например, адаптации к изменению условий функционирования объекта управления) , которое может осуществляться не коррекцией физической схемы регулятора, а программно;

• - возможность параллельного дистанционного компьютерного управления объектами многих локальных САР, что позволяет строить интегрированные системы автоматического управления технологическими комплексами.

Особенность применения цифровых устройств управления состоит в необходимости сопряжения непрерывного объекта, требующего зачастую непрерывных воздействий и имеющего непрерывную во времени реакцию, и дискретных (прерывных во времени и по величине) по своей природе цифровых устройств, оперирующих с численными значениями сигналов.

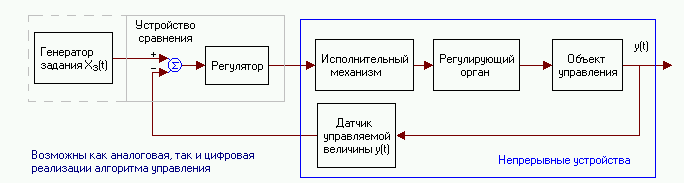
Рис. 2.1. Функциональная схема САР. Алгоритм управления (ПИ, ПИД и др.) может быть реализован как в аналоговой, непрерывной схемной форме, так и в цифровом виде, посредством компьютерной программы. В последнем случае временная последовательность цифровых значений, формируемых цифровым процессором, требует преобразования в непрерывный сигнал

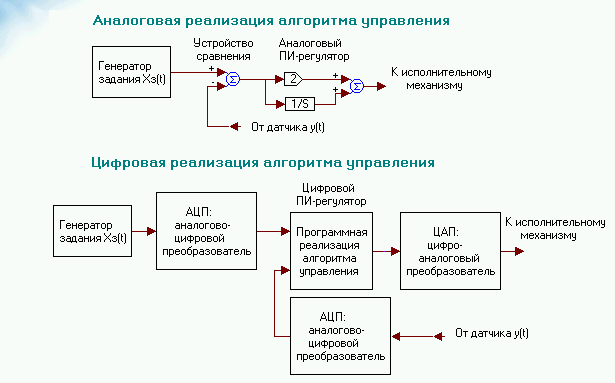
Рис. 2.2. Функциональные схемы аналоговой и цифровой реализаций алгоритма управления. В аналоговой реализации используются физические устройства: сумматор, интегратор и усилитель, в цифровой - устройства преобразования аналог- цифра и наоборот, и реализуемый в цифровом виде, т.е. в виде компьютерной программы алгоритм

АЦП преобразует непрерывные величины в периодические последовательности их цифровых отсчетов.

Цифровой процессор выполняет те же функции, что и аналоговый ПИ-регулятор: сравнивает задание и управляемую величину, численно интегрирует по времени ошибку регулирования и вычисляет пропорциональную ей величину, складывает их, получая эквивалентный непрерывному во времени регулятору сигнал, и в виде последовательности чисел отправляет результат на ЦАП.

ЦАП преобразует последовательность полученных числовых значений в плавную функцию времени.