IV. Інтегральне числення
Обчислити інтеграли
а)
=? б)
=
?
V. Елементи теорії поля
Довести формулу:
div(u∙ )= grad u ( -вектор, u=const)
----------------------------------------------------------------------------------------------------------
ВАРІАНТ 14
І. МАТРИЧНА АЛГЕБРА
Знайти обернену матрицю для матриці А.
;
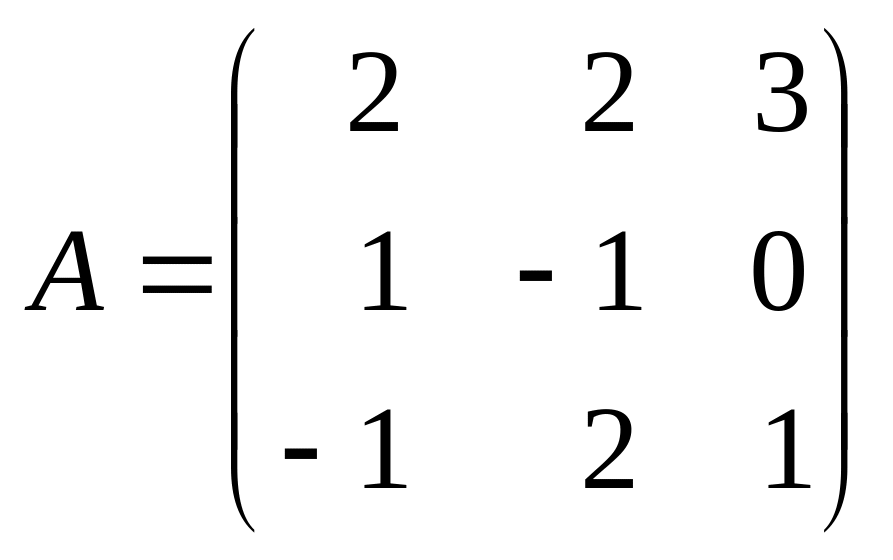ІІ. ВЕКТОРНА АЛГЕБРА
Знайти довжини сторін трикутника, координати вершин якого: 1) (4, – 5), (– 1, 7), (– 2, 3); 2) (2, –3), (8, 5), (– 7, – 3); 3) (0, 0), (15, 8), (5, –7); 4) (3, 0), (3, 11), (– 9, 16).
ІІІ. ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ
=?;
б)
=?;
IV. ІНТЕГРАЛЬНЕ ЧИСЛЕННЯ
Обчислити інтеграли
а)
=? б)
=
?
V. ЕЛЕМЕНТИ ТЕОРІЇ ПОЛЯ
Довести формулу:
rot( + )=rot +rot
----------------------------------------------------------------------------------------------------------
ВАРІАНТ 15
І. МАТРИЧНА АЛГЕБРА
Знайти
добуток матриць 
;
ІІ. ВЕКТОРНА АЛГЕБРА
Сторони прямокутника, які дорівнюють 8 і 15, є осями координат. Знайти довжину його діагоналі.
ІІІ. ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ
=?;
б)
=?;
IV. ІНТЕГРАЛЬНЕ ЧИСЛЕННЯ
Обчислити інтеграли
а)
=? б)
=
?
V. ЕЛЕМЕНТИ ТЕОРІЇ ПОЛЯ
Довести формулу:
rot(u∙ )=u rot( )+grad (u× ) (u=const)
----------------------------------------------------------------------------------------------------------
ВАРІАНТ 16
І. МАТРИЧНА АЛГЕБРА
Знайти
добуток матриць 
;
ІІ. ВЕКТОРНА АЛГЕБРА
Визначити довжини сторін чотирикутника, якщо координати його вершин такі: (1½, 2), (2, 2), (– 3, –10), (– 4½, – 6).
ІІІ. ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ
=?;
б)
=?;
IV. Інтегральне числення
Обчислити інтеграли
а)
=? б)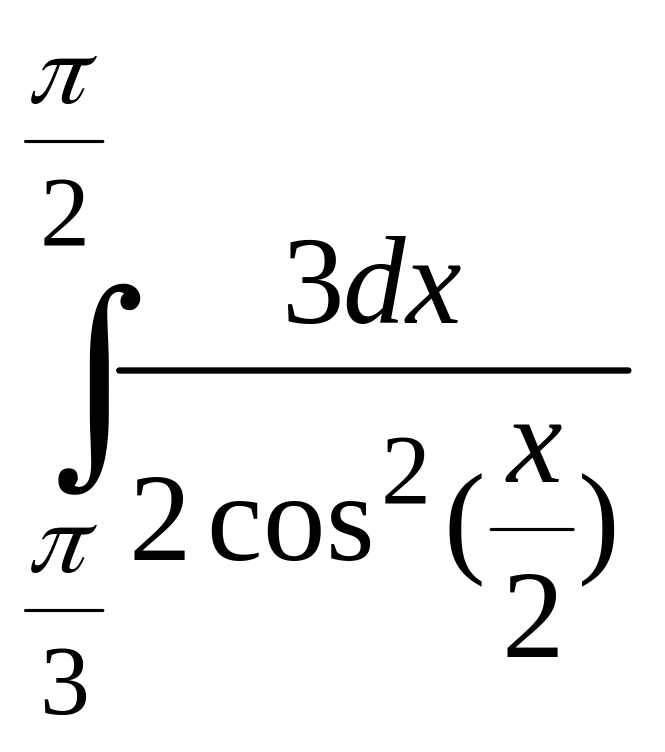
=
?
V. Елементи теорії поля
Довести формулу:
div( × )=b∙rot( ) - a∙rot
----------------------------------------------------------------------------------------------------------
ВАРІАНТ 17
І. МАТРИЧНА АЛГЕБРА
Знайти
добуток матриць 
;
ІІ. ВЕКТОРНА АЛГЕБРА
Знайти довжини діагоналей чотирикутника, коли відомі координати його вершин: (3, 5), (6, 9), (11, – 1), (– 3, – 3).
ІІІ. ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ
=?;
б)
=?;
IV. ІНТЕГРАЛЬНЕ ЧИСЛЕННЯ
Обчислити інтеграли
а)
=? б)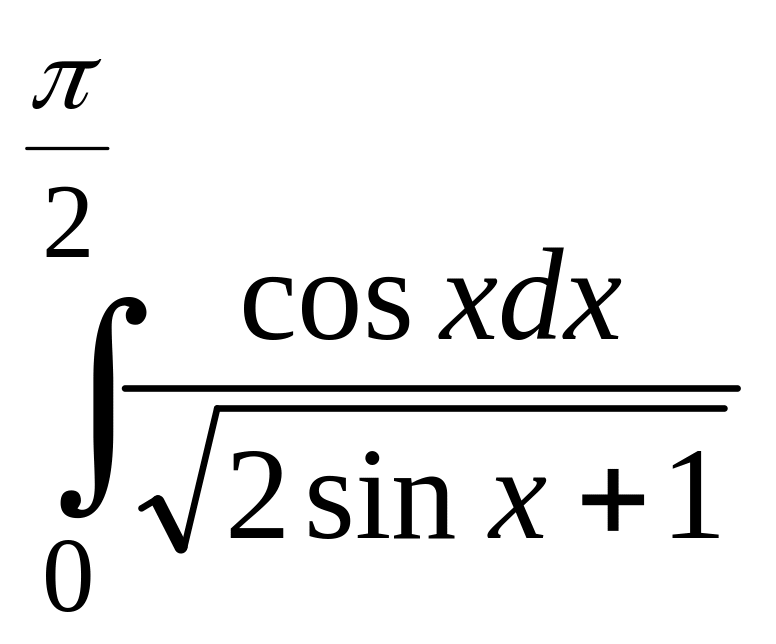
=
?
V. ЕЛЕМЕНТИ ТЕОРІЇ ПОЛЯ
Знайти:
div (ugrad u)=?
----------------------------------------------------------------------------------------------------------
ВАРІАНТ 18
І. МАТРИЧНА АЛГЕБРА
;
ІІ. ВЕКТОРНА АЛГЕБРА
Знайти у, якщо відстань точки (10, у) від точки (2, – 7) дорівнює 17.
ІІІ. ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ
=?; б)
=?;
IV. ІНТЕГРАЛЬНЕ ЧИСЛЕННЯ
Обчислити інтеграли
а)
=? б)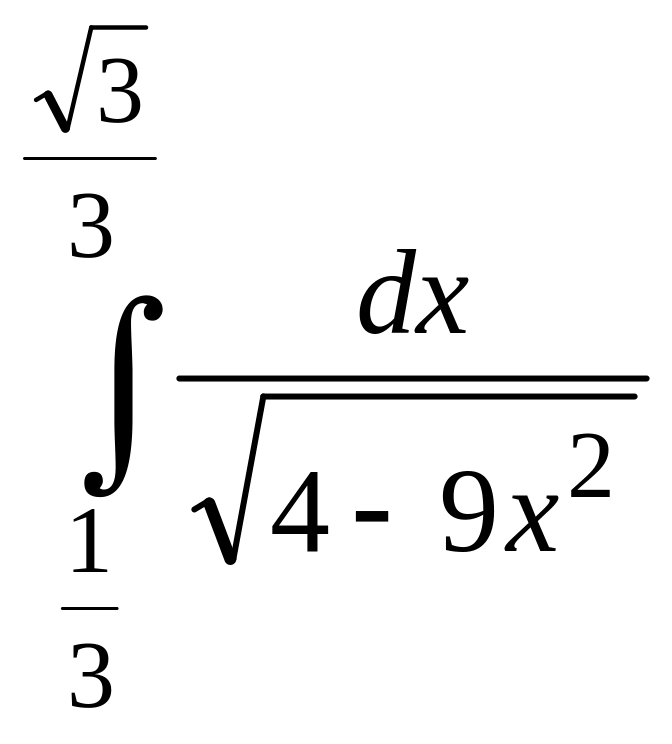
=
?
V. ЕЛЕМЕНТИ ТЕОРІЇ ПОЛЯ
Знайти div (ugrad v)=?
----------------------------------------------------------------------------------------------------------
ВАРІАНТ 19
І. МАТРИЧНА АЛГЕБРА
Знайти
добуток матриць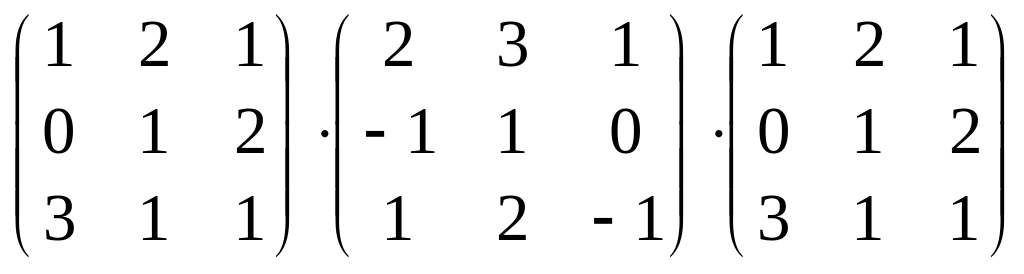 
;
ІІ. ВЕКТОРНА АЛГЕБРА
Знайти координати середини відрізка прямої, що сполучає точки: 1) (8, 3) і (4, – 5); 2) (– 5, 2) і (– 2, –4); 3) (1½,0) і (– 2½, 5).
ІІІ. ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ
=?;
б)
=?.
IV. ІНТЕГРАЛЬНЕ ЧИСЛЕННЯ
Обчислити інтеграли
а)
=? б)
=
?
V. ЕЛЕМЕНТИ ТЕОРІЇ ПОЛЯ
Знайти div (grad u)=?
----------------------------------------------------------------------------------------------------------
ВАРІАНТ 20
І. МАТРИЧНА АЛГЕБРА
Знайти
добуток матриць 
ІІ. ВЕКТОРНА АЛГЕБРА
Відстань між точками (3, 0) і (5, – 4) поділено на 4 рівні частини. Визначити координати точок поділу.
ІІІ. ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ
=?;
б)
4=?;
IV. ІНТЕГРАЛЬНЕ ЧИСЛЕННЯ
а)
=? б)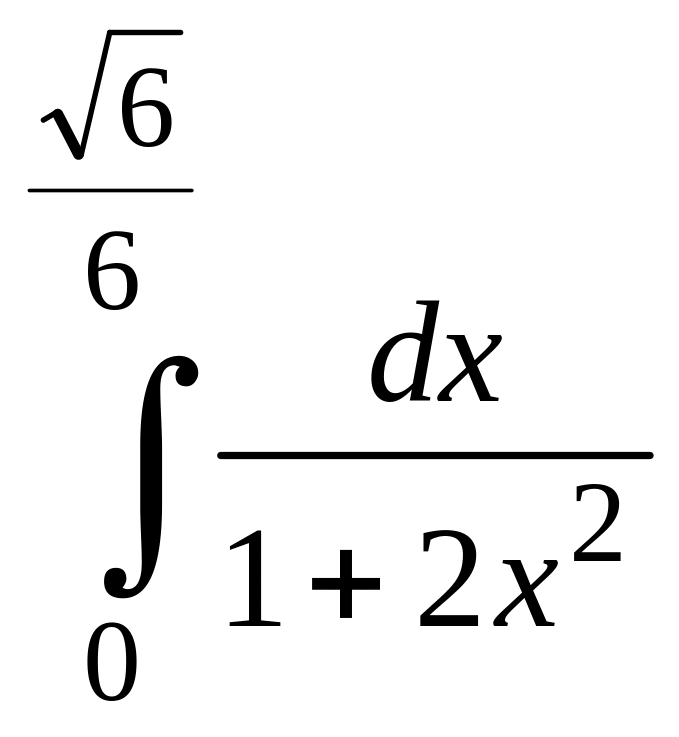
=
?
V. ЕЛЕМЕНТИ ТЕОРІЇ ПОЛЯ
Знайти rot(grad u)=?
----------------------------------------------------------------------------------------------------------
ВАРІАНТ 21
І. МАТРИЧНА АЛГЕБРА
Знайти невідому матрицю Х з рівняння:
;
ІІ. ВЕКТОРНА АЛГЕБРА
Вершинами трикутника є точки з координатами: (4, – 3), (– 3, –5), (0, 4). Знайти координати середин сторін трикутника.
ІІІ. ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ
=?; б)
=?;
IV. ІНТЕГРАЛЬНЕ ЧИСЛЕННЯ
а)
=? б)
=
?
V. ЕЛЕМЕНТИ ТЕОРІЇ ПОЛЯ
Знайти div rot( )=?
----------------------------------------------------------------------------------------------------------
ВАРІАНТ 22
І. МАТРИЧНА АЛГЕБРА
Знайти невідому матрицю Х з рівняння:
;
ІІ. ВЕКТОРНА АЛГЕБРА
Відстань між точками (х, 4) і (– 6, у) поділяється в точці (– 1, 1) пополам. Знайти ці точки.
ІІІ. ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ
=?;
б)
=?;
IV. ІНТЕГРАЛЬНЕ ЧИСЛЕННЯ
а)
=? б)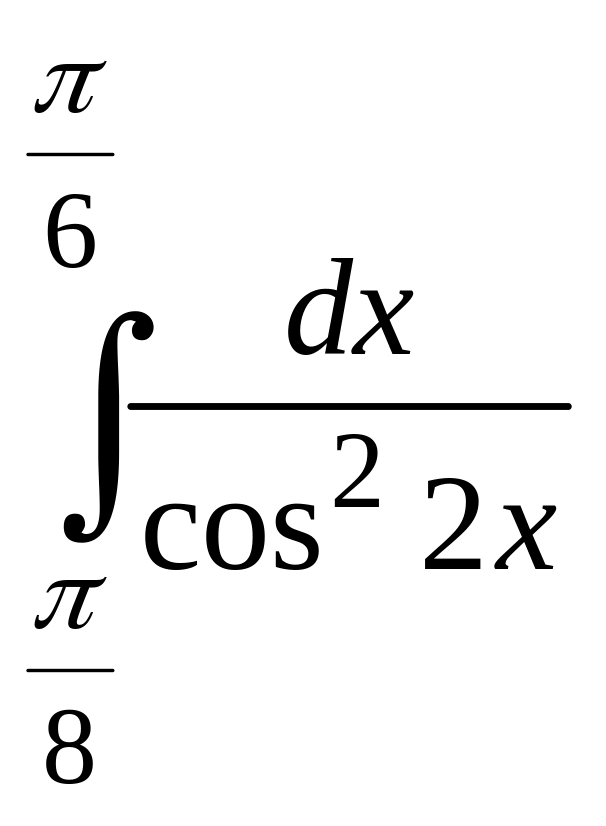
=
?
V. ЕЛЕМЕНТИ ТЕОРІЇ ПОЛЯ
Знайти rot( ∙f(r))= ?
----------------------------------------------------------------------------------------------------------
ВАРІАНТ 23
І. МАТРИЧНА АЛГЕБРА
Знайти невідому матрицю Х з рівняння:
;
ІІ. ВЕКТОРНА АЛГЕБРА
Відстань між точками (– 5, 2) і (х, у) поділяється в точці ( – 1½, – 1) пополам. Знайти координати х та у другої точки.
ІІІ. ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ
=?;
б)
=?;
IV. ІНТЕГРАЛЬНЕ ЧИСЛЕННЯ
а)
=? б)
=
?
V. ЕЛЕМЕНТИ ТЕОРІЇ ПОЛЯ
Знайти rot[ ×f(r)∙ ]= ?
----------------------------------------------------------------------------------------------------------
ВАРІАНТ 24
І. МАТРИЧНА АЛГЕБРА
Знайти невідому матрицю Х з рівняння:
;
ІІ. ВЕКТОРНА АЛГЕБРА
Вершинами трикутника є точки з координатами: (7, 4), (– 4, 6), (2, – 5). Знайти координати середин його медіан.
ІІІ. ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ
=?; б)
=?;
IV. ІНТЕГРАЛЬНЕ ЧИСЛЕННЯ
а)
=? б)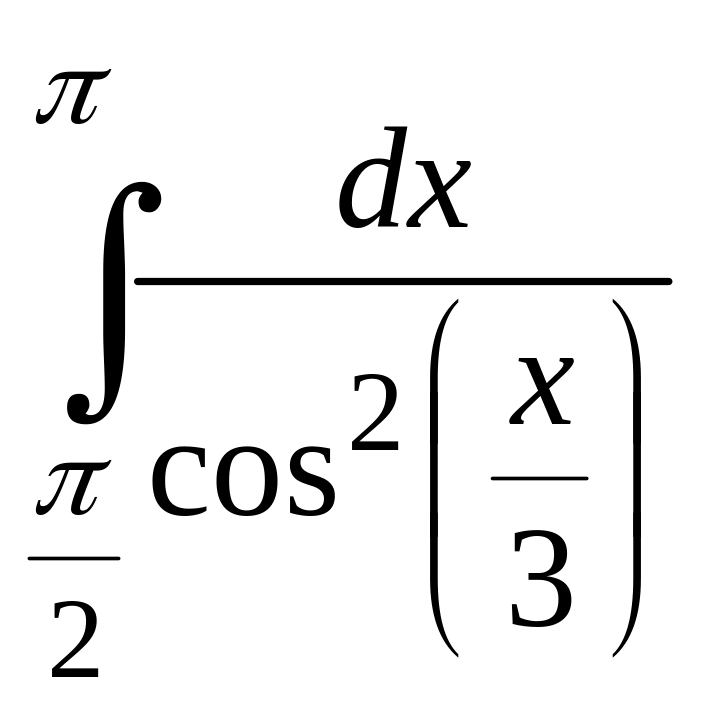
=
?
V. ЕЛЕМЕНТИ ТЕОРІЇ ПОЛЯ
Знайти rot = ?
----------------------------------------------------------------------------------------------------------
ВАРІАНТ 25
І. МАТРИЧНА АЛГЕБРА
Знайти невідому матрицю Х з рівняння:
.
ІІ. ВЕКТОРНА АЛГЕБРА
Координатами двох сусідніх вершин паралелограма є точки: (2, – 3) і (– 3, 4), а діагоналі його перетинаються в початку координат. Знайти координати двох інших вершин паралелограма.
ІІІ. ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ
=?;
б)
=?;